An Analysis of SAT-based Model Checking
Techniques in an Industrial Environment
Nina Amla, Xiaoqun Du, Andreas Kuehlmann, Robert P. Kurshan and
Kenneth L. McMillan
Cadence Design Systems
Abstract. Model checking is a formal technique for automatically ver-
ifying that a finite-state model satisfies a temporal property. In model
checking, generally Binary Decision Diagrams (BDDs) are used to effi-
ciently encode the transition relation of the finite-state model. Recently
mod el checking algorithms based on Boolean satisfiability (SAT) proce-
dures have b een developed to complement the traditional BDD-based
mod el checking. These algorithms can be broadly classified into three
categories: (1) bounded model checking which is useful for finding failures
(2) hybrid algorithms that combine SAT and BDD based methods for
unbounded model checking, and (3) purely SAT-based unbounded model
checking algorithms. The goal of this paper is to provide a uniform and
comprehensive basis for evaluating these algorithms. The paper describes
eight bounded and unbounded techniques, and analyzes the performance
of these algorithms on a large and diverse set of hardware benchmarks.
1 Introduction
A common method used in formal verification is model checking [7, 26]. Generally,
Binary Decision Diagrams (BDDs) [4] are used to symbolically represent the
set of states. This approach, known as symbolic model checking [5], has been
successfully applied in practice. Unfortunately, BDDs are very sensitive to the
type and size of the system. For instance common designs like multipliers can
not be r epres ented efficiently with BDDs. Due to recent advances in tools [19, 23,
11] that solve the Boolean satisfiability problem (SAT), formal reasoning based
on SAT is proving to be an viable alternative to BDDs.
Bounded Model Checking (BMC) [3] is a SAT-based technique where a sys-
tem is unfolded k times and encoded as a SAT problem to be solved by a
CNF-based SAT solver. A satisfying assignment returned by the SAT solver
corresponds to a counterexample of length k. If the problem is determined to
be unsatisfiable, the SAT solver produces a proof of the fact that there are no
counterexamples of length k. A different approach, called circuit-based BMC [15],
uses the circuit s tructure to make BMC more efficient. The circuit is unfolded
incrementally and at each step equivalent nodes are identified and merged to
simplify the circuit. BMC, while successful in finding errors, is incomplete: there
is no efficient way to decide that the property is true. Recently several complete
model checking algorithms have been developed that use SAT-based quantifier
elimination [20, 10], ATPG methods [12], and combinations of SAT-based BMC
with techniques like BDD-based model checking [6, 22], induction [27] and inter-
polation [21].
Since users have limited resources for the verification of systems, it is impor-
tant to know which of these new SAT-based algorithms is most effective. This
paper presents an experimental analysis of these bounded and unbounded algo-
rithms in an attempt to address this issue. Unlike previous efforts that compared
SAT-based BMC to BDD-based and explicit state methods (cf. [8, 1]), this pa-
per focuses only on SAT-based techniques. In Section 2 we give an overview of
the eight algorithms we evaluated. A more comprehensive survey of SAT-based
techniques can be found in [25]. We describe our experimental framework in
Section 3. We compare the various algorithms on a set of over 1000 examples
drawn from actual hardware designs. Section 4 presents our results and analysis.
We conclude and discuss future work in Section 5.
2 Overview of the Algorithms
2.1 Preliminaries
A model M = (S, I, T, L) has a set of states S, a set of initial states I ⊆ S, a
transition relation T ⊆ S × S, and a labeling function L : S → 2
A
where A is a
set of atomic propositions. For the purposes of this paper, we shall consider only
invariant properties specified in the logic LTL. The construction given in [16]
can be used to reduce model checking of safety properties to checking invariant
properties. The syntax and semantics of LTL and other temporal logics is not
given here but can be found in [9].
Given a finite state model M and a safety property p, the model checking
algorithm checks that M satisfies p, written M |= p. The forward reachability
algorithm starts at the initial states and computes the image, which is the set of
states reachable in one step. This procedure is continued until either the prop erty
is falsified in some state or no new states are encountered (a fixed point). The
backward reachability algorithm works similarly but starts from the states where
the property is false and computes the preimage, which is the set of states that
can reach the current states in one step. The representation and manipulation
of the sets of states can be done explicitly or with Binary Decision Diagrams
(BDDs). In the sequel, we shall refer to BDD-based model checking as MC.
2.2 DPLL-style SAT solvers
The Boolean satisfiability problem (SAT) is to determine if a given Boolean
formula has a satisfying assignment. This is generally done by converting the
formula into Conjunctive Normal Form (CNF), which can be efficiently solved
by a SAT solver. A key operation used in SAT solvers is resolution, where two
clauses (a ∨ b) and (¬a ∨ c) can be resolved to give a new clause (b ∨ c). Modern
DPLL-style SAT solvers [19, 23, 11] make assignments to variables, called deci-
sions, and generate an implication graph which records the decisions and the
effects of Boolean constraint propagation. When all the variables are assigned,
the SAT solver terminates with the satisfying assignment. But if there is a con-
flict, which is a clause where the negation of every literal already appears in the
implication graph, a conflict clause is generated through resolution. This conflict
clause is added to the formula to avoid making those assignments again. The
SAT solver then backtracks to undo some of the conflicting assignments. The
SAT solver terminates with an unsatisfiable answer when it rules out all possible
assignments. The resolution steps used in generating the conflict clauses can now
be used to produce a proof of unsatisfiability.
2.3 SAT-based Bounded Model Checking
Bounded Model Checking (BMC) [3] is a restricted form of model checking,
where one searches for a counterexample (CEX) in executions bounded by some
length k. In this approach the model is unfolded k times, conjuncted with the
negation of the property, and then encoded as a propositional satisfiability for-
mula. Given a model M and an invariant property p, the BMC problem is
encoded as follows:
BMC (M , p, k) = I(s
0
) ∧
k−1
^
i=0
T (s
i
, s
i+1
) ∧
k
_
i=0
¬p(s
i
)
The formula can be converted into CNF and solved by a SAT solver. If the
formula is satisfiable, then the property is false, and the SAT solver has found
a satisfying assignment that corresponds to a counterexample of length k. In
the unsatisfiable case, there is no counterexample of length k and a proof of
unsatisfiability can be obtained from the SAT solver.
2.4 Circuit-based Bounded Model Checking
In circuit-based BMC the circuit structure is exploited to enhance efficiency.
Rather than translating the problem into a CNF formula directly, circuit-based
BMC uses an intermediate representation, called And-Inverter Graphs (AIGs)
[15], that keeps the circuit structure. The use of AIGs allows the application of
the SAT-sweeping technique [14], where one identifies equivalent nodes using a
SAT solver and merges these equivalent nodes to simplify the circuit represented
by the AIG. Random simulation is used to pick candidate pairs of nodes that
have identical simulation results, and a SAT solver is used to check whether the
XOR of the two candidate nodes can ever be satisfied. If not, the nodes are
equivalent and can be merged to simplify the AIG. If the XOR of the nodes
is satisfiable, the SAT solver will give a witness that shows how the nodes can
obtain different values. This witness can be used to show the in-equivalence of
other nodes to reduce the number of candidate pairs for equivalence-finding.
After the completion of SAT-sweeping, the simplified AIG is translated into a
CNF formula for BMC.
2.5 CEX-based Abstraction Refinement
Counterexample-based abstraction-refinement [17] is an iterative technique that
starts with BDD-based MC on an initial conservative abstraction of the model.
If MC proves the property on the abstraction then the property is true on the
full model. However, if a counterexample A is found, it could either be an actual
error or it may be spurious, in which case one needs to refine the abstraction to
rule out this counterexample. The process is then repeated until the property is
found to be true, or until a real counterexample is produced.
The counterexample-based method in [6] used BMC to concretize the coun-
terexample by solving the following:
BMC (M , p, k, A) = I(s
0
) ∧
k−1
^
i=0
T (s
i
, s
i+1
) ∧
k
_
i=0
¬p(s
i
) ∧
k
^
i=0
A
i
where A
i
is a constraint that represents the assignments in the abstract coun-
terexample A in time frame i. If this formula is determined to be satisfiable then
the satisfying assignment represents a counterexample on the concrete model.
In the unsatisfiable case, the metho d [6] analyzes the proof of unsatisfiability
generated by the SAT solver to find a set of constraints whose addition to the
abstraction will rule out this spurious counterexample. Since the BMC problem
includes the constraints in the abstract counterexample A, one can guarantee
that A is eliminated by adding all variables that occur in the pro of to the existing
abstraction. The pseudocode is shown in Figure 1.
pro cedur e cex-based (M ,p)
1. generate initial abstraction M
0
2. while true do
3. if M C(M
0
, p) holds then return verified
4. let k = length of abstract counterexample A
5. if BMC(M,p,k,A) is SAT then return counterexample
6. else use proof of UNSAT P to refine M
0
7. end while
end
Fig. 1. SAT-based counterexample procedure
2.6 Proof-based Abstraction Refinement
The proof-based algorithm in [22] also iterates through SAT-based BMC and
BDD-based MC. It starts with a short BMC run, and if the problem is sat-
isfiable, an error has been found. If the problem is unsatisfiable, the proof of
unsatisfiability is used to guide the formation of a new conservative abstraction
on which BDD-based MC is run. In the case that the BDD-based model checker
proves the property then the algorithm terminates; otherwise the length k
0
of the
counterexample generated by the model checker is used as the next BMC length.
Notice that only the length of the counterexample generated by the BDD-based
MC is used. This method creates a new abstraction in each iteration, in contrast
to the counterexample metho d which refines the existing abstraction. Since this
abstraction includes all the variables in the proof of unsatisfiability for a BMC
run up to depth k, we know that any counterexample obtained from model
checking this abstract model will be of length greater than k. Therefore, unlike
the counterexample method, this algorithm eliminates all counterexamples of
length k in a single unsatisfiable BMC run. This procedure, shown in Figure 2,
is continued until either a failure is found in the BMC phase or the property is
proved in the BDD-based MC phase. The termination of the algorithm hinges
on the fact that the value of k
0
increases in every iteration.
pro cedur e proof-based (M,p)
1. initialize k
2. while true do
3. if BMC(M,p,k) is SAT then return counterexample
4. else
5. derive new abstraction M
0
from proof P
6. if M C(M
0
, p) holds then return verified
7. else set k to length of counterexample k
0
8. end while
end
Fig. 2. Proof-based pro cedure
2.7 Induction-based Model Checking
The induction-based method in [27] uses a SAT solver as the decision procedure
for a special kind of induction called k-induction. In this type of induction, one
attempts to prove that a property holds in the current state, assuming that it
holds in the previous k consecutive states. In addition, for completeness, one has
to add an additional constraint that specifies that the states along a path must
be unique. This is formalized as follows:
Base(M , p, k) = I(s
0
) ∧
k−1
^
i=0
T (s
i
, s
i+1
) ∧
k
_
i=0
¬p(s
i
)
Step(M , p, k) =
^
0≤i<j≤k
s
i
6= s
j
∧
k
^
i=0
T (s
i
, s
i+1
) ∧
k
^
i=0
p(s
i
) ∧ ¬p(s
k+1
)
A counterexample has been found if the base condition is satisfiable; other-
wise the value of k is increased until both conditions are unsatisfiable, which
means the property holds. The pseudocode is shown in Figure 3.
pro cedur e k-induction (M,p)
1. initialize k = 0
2. while true do
3. if Base(M, p, k) is SAT then return counterexample
4. else if Step(M, p, k) is UNSAT then return verified
5. k = k + 1
6. end while
end
Fig. 3. The k-induction procedure
2.8 Interpolation-based Model Checking
An interpolant I for an unsatisfiable formula A ∧ B is a formula such that: (1)
A ⇒ I (2) I ∧B is unsatisfiable and (3) I refers only to the common variables of
A and B. Intuitively, I is the set of facts that the SAT solver considers relevant
in proving the unsatisfiability of A ∧ B.
The interpolation-based algorithm [21] uses interpolants to derive an over-
approximation of the reachable states with respect to the property. This is done
as follows (Figure 4). The BMC problem BMC (M , p, k) is solved for an ini-
tial depth k. If the problem is satisfiable, a counterexample is returned, and
the algorithm terminates. If BMC (M , p, k) is unsatisfiable, the formula rep-
resenting the problem is partitioned into Pref (M , p, k) ∧ Suff (M , p, k), where
Pref (M , p, k) is the conjunction of the initial condition and the first transition,
and Suff (M , p, k) is the conjunction of the rest of the transitions and the final
condition. The interpolant I of Pref (M , p, k ) and Suff (M , p, k) is computed.
Since Pref (M , p, k) ⇒ I, it follows that I is true in all states reachable from
I(s
0
) in one step. This means that I is an over-approximation of the set of states
reachable from I(s
0
) in one step. Also, since I ∧ Suff (M , p, k) is unsatisfiable, it
also follows that no state s atisfying I can reach an error in k − 1 steps. I f I con-
tains no new states, that is, I ⇒ I(s
0
), then a fixed point of the reachable set of
states has been reached, thus the property holds. If I has new states then R
0
rep-
resents an over-approximation of the states reached so far. The algorithm then
uses R
0
to replace the initial set I, and iterates the process of solving the BMC
problem at depth k and generating the interpolant as the over-approximation
of the set of states reachable in the next step. The property is determined to
be true when the BMC problem with R
0
as the initial condition is unsatisfiable,
and its interpolant leads to a fixed point of reachable states. However, if the
BMC problem is satisfiable, the counterexample may be spurious since R
0
is
an over-approximation of the reachable set of states. In this case, the value of
k is increased, and the procedure is continued. The algorithm will eventually
terminate when k becomes larger than the diameter of the model.
pro cedur e interpolation (M, p)
1. initialize k
2. while true do
3. if BM C(M, p, k) is SAT then return counterexample
4. R = I
5. while true do
6. M
0
= (S, R, T, L)
7. let C = Pref (M
0
, p, k) ∧ Suff (M
0
, p, k)
8. if C is SAT then break (goto line 15)
9. /* C is UNSAT */
10. compute interpolant I of Pref (M
0
, p, k) ∧ Suff (M
0
, p, k)
11. R
0
= I is an over-approximation of states reachable from R in one step.
12. if R ⇒ R
0
then return verified
13. R = R ∨ R
0
14. end while
15. increase k
16. end while
end
Fig. 4. Interpolation procedure
2.9 Quantification-based Model Checking
There are many approaches [25] to doing quantifier elimination which is a key
step in reachability analysis. The purely SAT-based quantifier elimination pro-
cedure introduced in [20] works by enumeration of all the satisfying assignments.
The SAT solver is modified to generate all the satisfying assignments by adding
blocking clauses to the problem each time an assignment is found. The SAT
solving process is continued until no new solutions are found. A blocking clause,
which refers only to the state variables, represents the negation of a state cube.
This quantification procedure yields a purely SAT-based method for computing
the preimage in backward s ymbolic model checking.
A recent quantification-based method [10] uses a circuit representation of
the blocking constraints and use a hybrid solver that works directly on this
representation. This enables circuit cofactoring with respect to the input assign-
ments to simplify the circuit graph in each enumeration step. This results in
more solutions in each enumeration step and thus far fewer enumerations steps.
It is reported in [10] that this method outperforms the technique described in
[20]. We implemented the basic cofactoring-based quantification approach in our
framework. Our implementation did not include the heuristics provided in [10]
to select values for unassigned inputs in the satisfying cube; we just use the com-
plete input assignment provided by the SAT solver in that enumeration step. We
also did not use functional hashing in the simplification process but we did use
structural hashing.
2.10 ATPG-based Model Checking
Automatic Test Pattern Generation (ATPG) is an approach that adapts DPLL-
style SAT techniques to a structural representation of a circuit. The ATPG-based
algorithm in [12] combines the structure guided search strategy of ATPG with
the faster implication procedures and conflict-based learning in SAT solvers.
They use a circuit representation, a CNF clause database and a mapping between
both representations. The method conducts a backward search, using an ATPG-
based back-tracing traversal method, from the states where the property is false.
The search strategy, which is a mixture of DFS and BFS, is based on a cost
function that measures the number of states traversed. A counterexample is
generated if an initial state is reached during the search; otherwise the property
is proved to be true if the entire backward reachable set of states does not
intersect with the initial state set. This procedure is complete because the search
is efficiently bounded by using additional Boolean constraints to mark visited
states as already reached and hence never to be visited again.
3 Experimental Framework
In order to measure the relative performance of the algorithms described in
the previous section, we implemented all the methods except the ATPG-based
method SATORI, which was developed at University of Santa Barbara [12].
We developed a flexible experimental framework that allows external tools, like
SATORI, to be integrated with little effort. We use a simple intermediate repre-
sentation that can be translated easily and efficiently into the input language of
various tools. This interface also enables us to plug and play with different SAT
solvers and BDD packages.
3.1 Benchmarks
In the context of commercial software development, a good benchmark s uite must
be large, diverse, and representative of real customer designs. The data collection
must be fully automated, and must complete within a reasonable amount of time
so that the benchmark suite can be used as a regression suite for tracking the
performance of the software over time.
Our benchmark suite included approximately 85 hardware designs, accumu-
lated through many years of customer interaction. The sizes of these designs
ranged from a few hundred to more than 100,000 lines of HDL code. Each de-
sign in our benchmark suite contained from one up to a few hundred properties
to check. Some of the properties were duplicates because they were instanti-
ated from the same property declaration in similar parts of a design. To make
our benchmark suite as diverse as possible, we removed all duplicate proper-
ties, where two properties were considered duplicates if the model had the same
number of state and combinational variables, and that the running times were
within 10% of each other.
There were properties that none of the algorithms could finish within a rea-
sonable amount of time. We removed most of these properties from our bench-
mark suite because they were not useful for comparing the relative performance
of the algorithms. We did keep some of these properties to track performance
improvements of the algorithms over time. This resulted in a total of 1182 prop-
erties for the 85 designs in our benchmark suite. Out of these 1182 properties,
803 of them are passes, 364 of them are failures, and the remaining 15 properties
have unknown results.
3.2 Data collection
Each hproperty, algorithmi pair corresponds to one run for data collection. This
meant we needed 1182 runs for each technique, hence it was important that we
set up our test environment so that the experiments finished within a reasonable
amount of time. To do this, we set a time limit of 3600 seconds for each property.
We found in our experiments that a majority of the runs finished within this
time limit.
We used a computer server farm for data collection. In our experiments, we
use 10 identical Redhat Enterprise Linux machines, each with an AMD Opteron
CPU at 2GHZ and 4GB of available memory. We partitioned our entire set of
runs into multiple jobs, each job consisting of a small set of runs. These jobs are
submitted to the server farm and launched whenever a CPU is free. To ensure
the accurate collection of data, no other jobs are permitted on a CPU when it
is running one of our data collection jobs; also, a data collection job cannot be
started unless a machine has at least 4GB of free memory.
4 Results and Analysis
In our experiments, except for SATORI, we used the same SAT solver and BDD-
based model checker for all the techniques. The SAT solver is incremental [29],
in the sense that it is possible to add/delete clauses and restart the solver, while
maintaining all previously inferred conflict clauses that were not derived from
deleted clauses. An important point to note is that all methods were run with
default settings and there was no tuning done with respect to specific examples.
For the bounded model checking techniques, we set a time limit of 3600 sec-
onds and did four runs with depth limits of 10, 25, 50 and 100. We measured the
number of problems that were resolved within the time limit and the average

Depth # Props SAT-BMC CIR-BMC
# Fin Avg Time # Fin Avg Time
10 1182 1179 10.9 1178 15.0
25 1182 1175 28.8 1177 23.8
50 1182 1168 73.3 1170 53.3
100 1182 1153 174.0 1158 117.0
Table 1. Summary Table for the Bounded Techniques.
time taken per property (over all the properties regardless of whether an algo-
rithm finished or not) by both methods. Table 1 presents these results. We can
see that, after depth 25, the circuit-based approach takes less time on average.
We plot the run time at depth 100 for both algorithms in Figure 5, a point
below the diagonal line indicates that circuit BMC was faster on that example.
In all the tables and plots, the time for any unresolved property is taken to be
3600 seconds even if the method ran out of memory in far less time. The data
shows that the savings due to SAT sweeping in circuit-based BMC outweighs
the overhead at the larger depths.
0.1
1
10
100
1000
10000
0.1 1 10 100 1000 10000
CIRCUIT BMC time (seconds)
SAT BMC time (seconds)
0.1
1
10
100
1000
10000
0.1 1 10 100 1000 10000
kinduction time (seconds)
interpolation time (seconds)
Fig. 5. Plot of time in seconds. Left: X-axis is SAT BMC and Y-axis is Circuit BMC
at depth 100. Right: X-axis is Interpolation and Y-axis is K-induction.
For the unbounded techniques, we set a time limit of 3600 seconds for ver-
ification, and measure the number of problems that were resolved within this
time limit. Table 2 reports the number of resolved problems and average time
taken per property. As a baseline, we include the results for a forward traversal
BDD-based MC method in Table 2. It is interesting to note that all the SAT-
based algorithms, except the k-induction method, do better than BDD-based
model checking with respect to the number of problems resolved and average
time taken. However, we shall not include BDD-based MC in any further discus -
sions since it is not in the scope of this paper. We also see that the interpolation
method resolved more problems and had a lower average running time than the

other techniques. Since the interpolation method is the most robust, in the sense
that it resolves the largest number of problems, we plotted the run time of the
other five unbounded algorithms versus the interpolation algorithm. These are
shown in Figures 5 to 7. The plots indicate that in general the interpolation
method is faster and more robust than the other methods, however there are
still many cases where the other techniques do better.
Algorithm # Props # Resolved Total time Avg. Time
BDD 1182 876 1171716 991.3
pro of -based 1182 1121 269377 227.9
cex-based 1182 1054 520570 439.3
cofactor 1182 874 1154459 976.7
atpg-based 1182 992 756480 640.0
kinduction 1182 513 2417662 2045.4
interpolation 1182 1157 118791 100.5
Table 2. Summary Table for the Unbounded Techniques.
Tables 3 and 4 present the number of problems resolved, average time, aver-
age final depth and average number of state variables (size), for only the resolved
failing and passing problems respectively. The depth information was not avail-
able for the ATPG-based method and is therefore excluded from both tables. We
also r eport the number of “wins” with respect to time, where a win is attributed
to a particular algorithm if it does better than all others with respect to running
time. In the case of a tie, which we defined to be two runs where the difference
was less than 5% of the run time, we award a win for both metho ds.
0.1
1
10
100
1000
10000
0.1 1 10 100 1000 10000
cex-based time (seconds)
interpolation time (seconds)
0.1
1
10
100
1000
10000
0.1 1 10 100 1000 10000
proof-based time (seconds)
interpolation time (seconds)
Fig. 6. Plot of time in seconds. Left: X-axis is Interpolation and Y-axis is CEX-based.
Right: X-axis is Interpolation and Y-axis is Proof-based.

The failing properties in our benchmark suite can be roughly characterized
with respect to depth as follows: 91% failed at a depth of 25 or less with 24% of
the failures at a depth of 2, 7% failed between a depth of 26 till 100 and 2% failed
at a depth greater than 100. The data in Table 3 for the bounded techniques
is cumulative, in the sense that we report the total running time at depths 10,
25 and 50 for an err or found at depth 45. Since the maximum depth checked
was 100, the bounded techniques were not able to find failures that occurred at
depths greater than 100 and this is reflected in the number of failures. Table
3 shows some interesting trends for the failing properties. Not surprisingly we
see that, with respect to aver age run time, both bounded techniques do better
than all others on the failing properties. However, since the bounded techniques
were employed at fixed depths, this made finding the shallow errors, like the
failures at depth 2, more exp ens ive than necessary. The interpolation and proof-
based techniques are competitive with the bounded techniques in number of wins
but the proof-based technique is clearly the faster of the two. The k-induction
method is effective in finding the shallow failures, as is evident in the low run
time when it does resolve a problem. The correspondingly low depth numbers
in Table 3 are due to the fact that the k-induction method ran out of memory
fairly early in 662 cases. The mixed DFS/BFS search strategy of the ATPG-
based metho d could cause the technique to miss errors if it chooses to do DFS
early and may explain why it does poorly on failures. This is consistent with
the results reported in [24] which show that a purely BFS search is more robust
than a purely DFS search on failing properties. Another possibility is that, on
these examples, the set of s tates grows faster with backward exploration than
with forward exploration. This could in part explain why the cofactoring method
does poorly as well. Both the ATPG and cofactoring methods have a much lower
average size which suggests that these methods are unable to resolve the larger
examples.
Algorithm Failures
# Props # Wins Avg Time Avg Size Avg Depth
sat-bmc 351 230 9.6 106 15
circuit-bmc 350 219 14.1 106 15
pro of -based 359 216 22.1 111 19
cex-based 341 119 58.6 88 17
cofactor 268 157 71.8 60 18
atpg-based 295 144 119.6 54 -
kinduction 340 171 17.6 97 7
interpolation 362 224 31.6 112 16
Table 3. Summary Table for the Failing Properties.
For the passing properties, the interpolation technique is the fastest and
solves more properties than the other metho ds. The proof-based technique is

Algorithm Passes
# Props # Wins Avg Time Avg Size Avg Depth
pro of -based 762 380 54.9 115 30
cex-based 713 237 51.7 101 23
cofactor 606 457 48.0 109 7
atpg-based 697 427 53.4 111 -
kinduction 173 107 19.1 14 14
interpolation 795 701 21.9 130 22
Table 4. Summary Table for the Passing Properties.
the closest in terms of the number of properties resolved but is significantly
slower on average. We see that the proof-based method does better than the
counterexample-based method, despite the fact that the counterexample-based
method proves properties at lower depths on average. This is largely due to the
number of iterations done by the counterexample-based method, most of them
done refuting counterexamples at the same depth (see [2] for a detailed analysis).
The data in Table 4 indicates that the interpolation method is able to prove the
properties at a lower depth than the proof-based method. This suggests that the
approximate image computation is more effective on these examples than the cor-
responding BDD-based MC phase in the proof-based method. The k-induction
method does rather poorly since checking the k-induction step is expensive as
the value of k gets larger. As mentioned earlier, the size of the BMC problem for
the step case is often too large causing the SAT-solver to run out of memory. As
reported in [18], removing the simple path constraints and trading completeness
for efficiency may improve the performance of this method. The ATPG-based
and cofactoring methods have a high number of wins and are comparable to the
proof-based method in running time. Both methods do backward reachability
and cube enlargement but, while their performance signatures are similar, the
ATPG method appears to be more robust. The cofactoring method has a low
average depth which seems to suggest that a large and rapidly growing back-
ward reachable state space could be contributing to the difference. The search
strategy of ATPG-based method permits on-the-fly pruning of the search space,
which could be beneficial in such situations. However, we do not have enough
data on the ATPG method to validate this conjecture. Furthermore, as observed
in [10], using the heuristics to enlarge the satisfying state set in the cofactoring
technique has a significant impact on performance.
5 Conclusions and Future Work
This paper compares eight bounded and unbounded SAT-based algorithms on
a large set of industrial benchmarks. Our experiments show that although the
interpolation technique is the most efficient and robust over all, there were still
many examples where the other techniques did better. This is evident in the
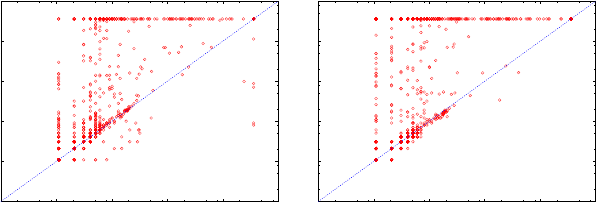
0.1
1
10
100
1000
10000
0.1 1 10 100 1000 10000
ATPG time (seconds)
interpolation time (seconds)
0.1
1
10
100
1000
10000
0.1 1 10 100 1000 10000
cofactoring-based time (seconds)
interpolation time (seconds)
Fig. 7. Plot of time in seconds. Left: X-axis is Interpolation and Y-axis is ATPG-based.
Right: X-axis is Interpolation and Y-axis is Cofactoring-based.
number of wins in Tables 3 and 4. Therefore, it would be useful to find ways
to apply the best algorithm for each task. One way to do this is to run the
algorithms in parallel and terminate the slower ones as soon as the first finishes.
Another approach would be to combine the various algorithms in a way that
exploits their strengths, like the hybrid method in [2] that combines the proof-
based and counterexample-based methods.
For future work, we plan to integrate the VIS model checker into our exper-
imental framework. We believe that methods implemented in VIS would pro-
vide some interesting comparisons. The conjecture that the simple path restric-
tion in k-induction hinders performance could be evaluated by using the more
sophisticated technique described in [18]. Furthermore, we could compare the
counterexample-based technique in [28] that uses a generalized counterexample
that is derived from the sequence of reachable states approximations computed
by the model checker. Finally it would be useful to evaluate the circuit-based
BMC solver described in [13] which uses BDDs to help in the solution of SAT
instances given in CNF.
Acknowledgments: The authors thank Kwang-Ting Cheng, Feng Lu, Ganap-
athy Parthasarthy and Madhu Iyer for help in integrating SATORI.
References
1. N. Amla, R. Kurshan, K. McMillan, and R. Medel. Exp erimental analysis of
different techniques for b ounded model checking. In TACAS, 2003.
2. N. Amla and K. McMillan. A hybrid of counterexample-based and proof-based
abstraction. In FMCAD, 2004.
3. A. Biere, A. Cimatti, E. Clarke, and Y. Zhu. Symbolic model checking without
BDDs. In TACAS, 1999.
4. R. E. Bryant. Graph-based algorithms for boolean function manipulations. IEEE
Transactions on Computers, 1986.
5. J. R. Burch, E. M. Clarke, K. L. McMillan, D.L. Dill, and J. Hwang. Symbolic
mod el checking: 10
20
states and beyond. In LICS, 1990.
6. P. Chauhan, E. Clarke, J. Kukula, S. Sapra, H. Veith, and D. Wang. Automated
abstraction refinement for model checking large state spaces using sat based conflict
analysis. In FMCAD, 2002.
7. E.M. Clarke and E. A. Emerson. Design and synthesis of synchronization skeletons
using branching time temporal logic. In Workshop on Logics of Programs, 1981.
8. F. Copty, L. Fix, R. Fraer, E. Giunchiglia, G. Kamhi, A. Tacchella, and M. Vardi.
Benefits of bounded model checking at an industrial setting. In CAV, 2001.
9. E. A. Emerson. Temporal and modal logic. In Handbook of Theo retical Computer
Science, Volume B: Formal Models and Sematics, 1990.
10. M. Ganai, A. Gupta, and P. Ashar. Efficient SAT-based unbounded symbolic
mod el checking using circuit cofactoring. In ICCAD, 2004.
11. E. Goldb erg and Y. Novikov. Berkmin: A fast and robust sat-solver. In DATE,
2002.
12. M. Iyer, G. Parthasarathy, and K.T. Cheng. SATORI- an efficient sequential SAT
solver for circuits. In ICCAD, 2003.
13. H. Jin and F. Somenzi. CirCUs: Hybrid satisfiability solver. In SAT, 2004.
14. A. Kuehlmann. Dynamic transition relation simplification for bounded property
checking. In ICCAD, 2004.
15. A. Kuehlmann, V. Paruthi, F. Krohm, and M. Ganai. Robust Boolean reasoning
for equivalence checking and functional property verification. In TCAD, 2003.
16. O. Kupferman and M. Vardi. Model checking of safety properties. In Formal
Methods in System Design, 2001.
17. R. Kurshan. Computer-aided Verification of Coordinating Processes: The
Automata-Theoretic Approach. Princeton University Press, 1994.
18. B. Li, C. Wang, and F. Somenzi. A satisfiability-based approach to abstraction
refinement in model checking. In Workshop on BMC, 2003.
19. J. Marques-Silva and K. Sakallah. GRASP: A search algorithm for propositional
satisfiability. IEEETC: IEEE Transactions on Computers, 48, 1999.
20. K. McMillan. Applying SAT methods in unbounded symbolic model checking. In
CAV, 2003.
21. K. McMillan. I nterpolation and SAT-based model checking. In CAV, 2003.
22. K. McMillan and N. Amla. Automatic abstraction w ithout counterexamples. In
TACAS, 2003.
23. M. W. Moskewicz, C. F. Madigan, Y. Zhao, L. Zhang, and S. Malik. Chaff: Engi-
neering an Efficient SAT Solver. In DAC, 2001.
24. G. Parthasarathy, M. Iyer, K.T. Cheng, and L.C. Wang. A comparison of BDDs,
BMC, and sequential SAT for model checking. In High-Level Design Validation
and Test Workshop, 2003.
25. M. Prasad, A. Biere, and A. Gupta. A survey of recent advances in sat-based
formal verification. In STTT, 2005.
26. J.P. Queille and J. Sifakis. Specification and verification of concurrent systems in
CESAR. In Proc. of the 5th International Symposium on Programming, 1982.
27. M. Sheeran, S. Singh, and G. Stalmarck. Checking safety properties using induction
and a SAT-solver. In FMCAD, 2000.
28. C. Wang, B. Li, H. Jin, G. Hachtel, and F. Somenzi. Improving ariadne’s bundle
by following multiple threads in abstraction refinement. In ICCAD, 2003.
29. J. Whittemore, J. Kim, and K. Sakallah. Satire: A new incremental satisfiability
engine. In DAC, 2001.
