z-SCORES
Frances Chumney, PhD
CONTENT OUTLINE
Overview of z-Scores
Probability & Normal Distribution
Distribution of Sample Means
Z-SCORES 2
OVERVIEW OF Z-SCORES
Z-SCORES 3
OVERVIEW OF z-SCORES
Student A earned a score of 76 on an exam
How many points were possible?
o 76 out of 80? Not bad!
o 76 out of 100? Not so great!
How does a score of 76 compare to other students?
o 76 the lowest score in the class?
o Anyone earn a score higher than 76?
Z-SCORES 4
OVERVIEW OF z-SCORES
z-Score
standardized value that specifies the exact location of
an X value within a distribution by describing its distance from
the mean in terms of standard deviation units
Standard Deviation Unit
Standardized value
1 SD unit = value of 1 SD before standardization
Z-SCORES 5
OVERVIEW OF z-SCORES
Z-SCORES 6
SCORE LOCATION
z-Scores describe the exact location of a score within a distribution
Sign: Whether score is above (+) or below (-) the mean
Number: Distance between score and mean in standard deviation units
Example
z = +1.00
o Sign: positive (+) so score is above the mean
o Number: 1.00 SD units from the mean
Z-SCORES 7
SCORE LOCATION
Example
z = - .50
o Sign: negative (-) so score is below the mean
o Number: .50 SD units from the mean
Z-SCORES 8
FORMULA: RAW SCORE → Z-SCORE
Transform raw score (X value) to z-Score
Numerator = Deviation Score
Denominator = Standard Deviation
s
MXX
z
Z-SCORES 9
FORMULA: RAW SCORE → Z-SCORE
Example
Population A has μ = 5 and σ = 1
Find z-Score for X = 3
z = (3-5) / 1 = -2/1 = -2
X
z
Z-SCORES 10
FORMULA: RAW SCORE → Z-SCORE
Example
Sample B has M = 5 and s = 1
Find z-Score for X = 5.5
z = (5.5-5) / 1 = .5/1 = +.5
s
MX
z
Z-SCORES 11
FORMULA: RAW SCORE → Z-SCORE
Transform z-Score to X value (raw score )
4 pieces of information:
o X = raw score
o μ or M = population/sample mean
o z = z-Score
o σ or s = population/sample standard deviation
zsMzX
Z-SCORES 12
FORMULA: RAW SCORE → Z-SCORE
Example
Person A from Sample Y has a z-Score of -.75
μ = 10, σ = 2
Find X for z-Score = -.75
o X = 10 + (-.75)(2) = 8.5
zsMzX
Z-SCORES 13
RELATIONSHIPS
z-Scores establish relationships between score, mean, standard deviation
Example
o Population: μ = 65 and X = 59 corresponds to z = -2.00
o Subtract 65 from 59 and find deviation score of six points corresponds to z value
of -2.00
o (X - μ) / z = σ
Example
o Population: σ = 4 and X = 33 corresponds to z = +1.50
o Multiply σ by z to find deviation score (4 * 1.5 = 6)
o Add/Subtract deviation score from X to find μ (33 – 6 = 27)
Z-SCORES 14
DISTRIBUTION TRANSFORMATIONS
Standardized Distribution
distribution composed of scores that have been transformed to
create predetermined values for μ and σ; distributions used
to make dissimilar distributions comparable
Properties/Characteristics
Same shape as original distribution – scores are renamed, but location in
distribution remains same
Mean will always equal zero (0)
Standard deviation will always equal one (1)
Z-SCORES 15
DISTRIBUTION TRANSFORMATIONS
How-To
Transform all X values into z-Scores z-Score Distribution
Advantage
Possible to compare scores or individuals from different distributions
Results more generalizable
o z-Score distributions have equal means (0) and standard deviations (1)
Z-SCORES 16
STANDARDIZED DISTRIBUTIONS
z-Score distributions include positive and negative numbers
Standardize to distribution with predetermined μ and σ to avoid negative
values
Procedure
Transform raw scores to z-scores
Transform z-scores into new X values with desired μ and σ values
Z-SCORES 17
STANDARDIZED DISTRIBUTIONS
Example
Population distribution with μ = 57 and σ = 14
Transform distribution to have μ = 50 and σ = 10
Calculate new X values for raw scores of X = 64 and X = 43
Step 1 (of 2)
o Transform raw scores to z-scores
• z = (X – μ) / σ
z = (64 – 57) / 14 = (7 / 14) = .50
z = (43 – 57) / 14 = (-14 / 14) = -1.0
Z-SCORES 18
STANDARDIZED DISTRIBUTIONS
Example (continued)
Step 2 (of 2)
o Transform to new X values
• z = .50 corresponds to a score ½ of a standard deviation above the mean
• In new distribution, z = .50 corresponds to score 5 points above mean (X = 55)
• In new distribution, z = -1.00 corresponds to score 10 points below mean (X = 40)
Z-SCORES 19
PROBABILITY & NORMAL
DISTRIBUTION
using the unit normal table to find proportions
Z-SCORES 20
PROBABILITY & NORMAL DISTRIBUTION
Z-SCORES 21
PROBABILITY & NORMAL DISTRIBUTION
Example
p(X > 80) = ?
o Translate into a proportion question: Out of all possible adult heights, what
proportion consists of values greater than 80”?
o The set of “all possible adult heights” is the population distribution
o We are interested in all heights greater than 80”, so we shade in the area of the
graph to the right of where 80” falls on the distribution
Z-SCORES 22
PROBABILITY & NORMAL DISTRIBUTION
Example (continued)
Transform X = 80 to a z-score
z = (X – μ) / σ = (80 – 68) / 6 = 12 / 6 = 2.00
Express the proportion we are trying to find in terms of the z-score: p(z
> 2.00) = ?
By Figure 6.4, p(X > 80) = p(z > +2.00) = 2.28%
Z-SCORES 23
UNIT NORMAL TABLE
Z-SCORES 24
UNIT NORMAL TABLE
Z-SCORES 25
UNIT NORMAL TABLE: GUIDELINES
Body = Larger part of the distribution
Tail = Smaller part of the distribution
Distribution is symmetrical Proportions to right of mean are symmetrical
to (read as “the same as”) those on the left side of the mean
Proportions are always positive, even when z-scores are negative
Identify proportions that correspond to z-scores or z-scores that
correspond to proportions
Z-SCORES 26
UNIT NORMAL TABLE: COLUMN
SELECTION
Proportion in Body = Column B
Mean
z
B
Z-SCORES 27
UNIT NORMAL TABLE: COLUMN
SELECTION
Proportion in Tail = Column C
Mean
z
C
Z-SCORES 28
UNIT NORMAL TABLE: COLUMN
SELECTION
Proportion between Mean & z = Column D
Mean
z
D
Z-SCORES 29
PROBABILITIES, PROPORTIONS, Z
Unit Normal Table
Relationships between z-score locations and proportions in a normal
distribution
If proportion is known, use table to identify z-score
Probability = Proportion
Z-SCORES 30
FIND PROPORTION/PROBABILITY
Example:
Column B
o What proportion of normal distribution corresponds to z-scores < z = 1.00?
o What is the probability of selecting a z-score less than z = 1.00?
(A)
(B) (C) (D)
z
Proportion
in Body
Proportion
in Tail
Mean and z
1.00
0.8413 0.1587 0.3413
0 1.00
Answer:
p(z < 1.00) = .8413 (or 84.13%)
Z-SCORES 31
FIND PROPORTION/PROBABILITY
Example:
Column B
o What proportion of a normal distribution corresponds to z-scores > z = -1.00?
o What is the probability of selecting a z-score greater than z = -1.00?
(A)
(B) (C) (D)
z
Proportion
in Body
Proportion
in Tail
Mean and z
1.00
0.8413 0.1587 0.3413
0 -1.00
Answer:
p(z > -1.00) = .8413 (or 84.13%)
Z-SCORES 32
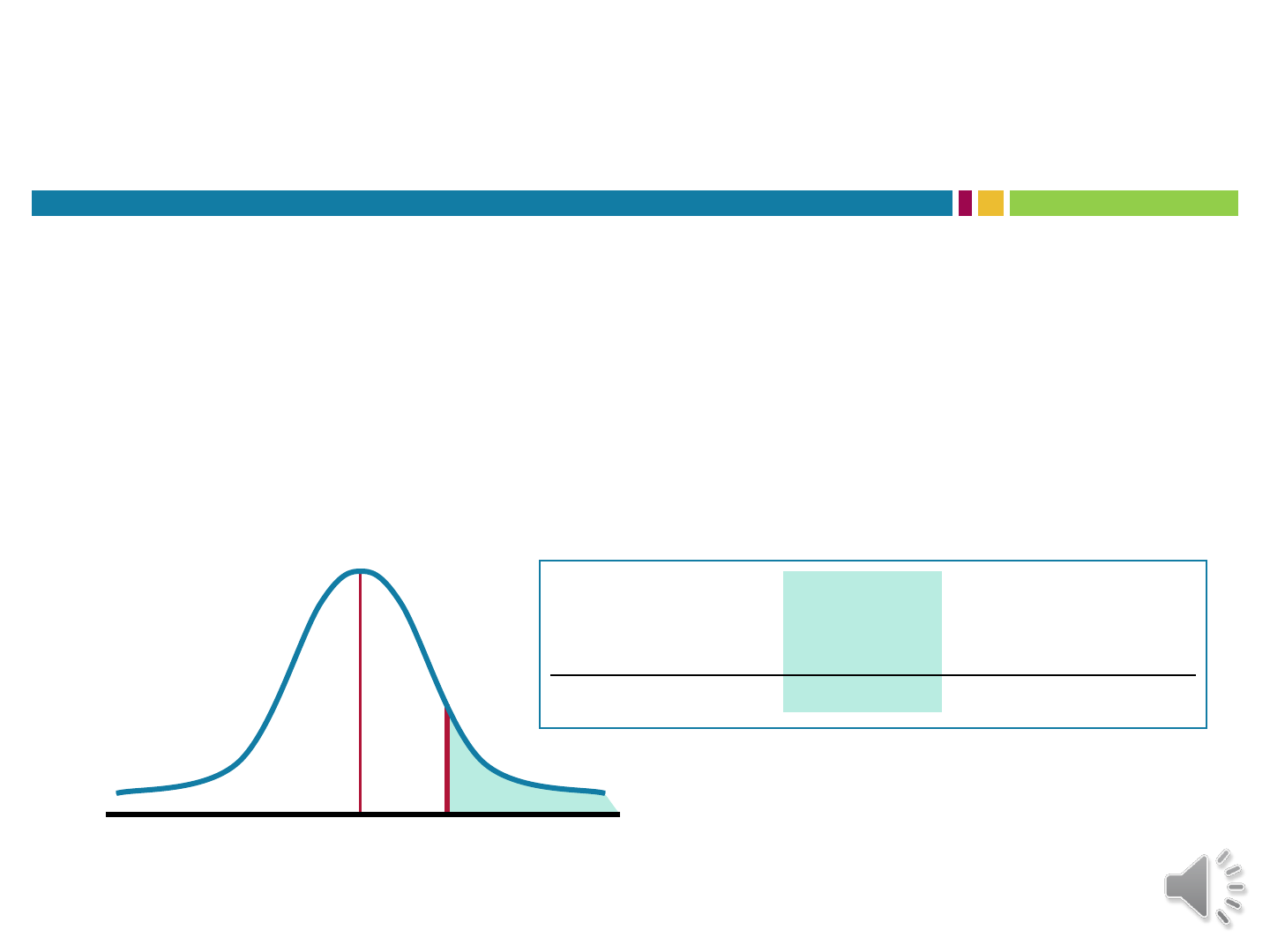
FIND PROPORTION/PROBABILITY
Example:
Column C
o What proportion of a normal distribution corresponds to z-scores > z = 1.00?
o What is the probability of selecting a z-score value greater than z = 1.00?
(A)
(B) (C) (D)
z
Proportion
in Body
Proportion
in Tail
Mean and z
1.00
0.8413 0.1587 0.3413
0 1.00
Answer:
p(z > 1.00) = .1587 (or 15.87%)
Z-SCORES 33
FIND PROPORTION/PROBABILITY
Example:
Column C
o What proportion of a normal distribution corresponds to z-scores > z = 1.00?
o What is the probability of selecting a z-score value greater than z = 1.00?
(A)
(B) (C) (D)
z
Proportion
in Body
Proportion
in Tail
Mean and z
1.00
0.8413 0.1587 0.3413
0 1.00
Answer:
p(z > 1.00) = .1587 (or 15.87%)
Z-SCORES 34
FIND PROPORTION/PROBABILITY
Example:
Column C
o What proportion of a normal distribution corresponds to z-scores < z = -1.00?
o What is the probability of selecting a z-score value less than z = -1.00?
(A)
(B) (C) (D)
z
Proportion
in Body
Proportion
in Tail
Mean and z
1.00
0.8413 0.1587 0.3413
0 -1.00
Answer:
p(z < -1.00) = .1587 (or 15.87%)
Z-SCORES 35
FIND PROPORTION/PROBABILITY
Example:
Column D
o What proportion of normal distribution corresponds to
positive z-scores < z = 1.00?
o What is the probability of selecting a positive z-score less than z = 1.00?
(A)
(B) (C) (D)
z
Proportion
in Body
Proportion
in Tail
Mean and z
1.00
0.8413 0.1587 0.3413
0 1.00
Answer:
p(0 < z < 1.00) = .3413 (or 34.13%)
Z-SCORES 36
FIND PROPORTION/PROBABILITY
Example:
Column D
o What proportion of a normal distribution corresponds to
negative z-scores > z = -1.00?
o What is the probability of selecting a negative z-score greater than z = -1.00?
(A)
(B) (C) (D)
z
Proportion
in Body
Proportion
in Tail
Mean and z
1.00
0.8413 0.1587 0.3413
0 -1.00
Answer:
p(0 < z < 1.00) = .3413 (or 34.13%)
Z-SCORES 37
FIND PROPORTION/PROBABILITY
Example:
Column D
o What proportion of a normal distribution corresponds to z-scores within 1
standard deviation of the mean?
o What is the probability of selecting a z-score greater than z = -1.00 and less than
z = 1.00 ?
(A)
(B) (C) (D)
z
Proportion
in Body
Proportion
in Tail
Mean and z
1.00
0.8413 0.1587 0.3413
0 -1.00
Answer:
.3413 + .3413 = .6826
p(-1.00 < z < 1.00) = .6826 (or 68.26%)
1.00
Z-SCORES 38
FIND Z-SCORE
Example:
Column B
o What z-score separates the bottom 80% from the remainder of the distribution?
(A)
(B) (C) (D)
z
Proportion
in Body
Proportion
in Tail
Mean and z
0.84
0.7995 0.2005 0.2995
0
Answer:
80% (or .8000) z = .84
z = ?
80% (or .8000)
20%
(.2000)
Z-SCORES 39
FIND Z-SCORE
Example:
Column C
o What z-score separates the top 20% from the remainder of the distribution?
(A)
(B) (C) (D)
z
Proportion
in Body
Proportion
in Tail
Mean and z
0.84
0.7995 0.2005 0.2995
0
z = ?
Answer:
20% (or .2000) z = .84
20%
(.2000)
Z-SCORES 40
FIND Z-SCORE
Example:
Column D
o What z-score separates the middle 60% from the remainder of the distribution?
(A)
(B) (C) (D)
z
Proportion
in Body
Proportion
in Tail
Mean and z
0.84
0.7995 0.2005 0.2995
0
z
Answer:
60% (or .6000) z = .84
z = ?
60% (or .6000)
30%
(.3000)
30%
(.3000)
z = ?
Z-SCORES 41
PROPORTION/PROBABILITY FOR X
Steps
Convert X to z-Score
Use Unit Normal Table to convert z-score to corresponding
percentage/proportion
Example
Assume a normal distribution with μ = 100 and σ = 15
What is the probability of randomly selecting an individual with an IQ score
less than 130?
p(X < 130) = ?
Step 1: Convert X to z-Score
Z-SCORES 42
00.2
15
30
15
100130
X
z
PROPORTION/PROBABILITY FOR X
Example (continued)
Step 2: Use Unit Normal Table to convert z-score to corresponding
percentage/proportion
z = 2.00
(A)
(B) (C) (D)
z
Proportion
in Body
Proportion
in Tail
Mean and z
2.00
0.9772 0.0228 0.4772
0
z
2.00
Answer:
p(X < 130) = .9772 (or 97.72%)
μ = 100
X=130
Z-SCORES 43
PROPORTION/PROBABILITY FOR X
Example
Assume a normal distribution with μ = 58 and σ = 10 for average speed of
cars on a section of interstate highway
What proportion of cars traveled between 55 and 65 miles per hour?
p(55 < X < 65) = ?
Step 1: Convert X values to z-Scores
30.
10
3
10
5855
X
z
70.
10
7
10
5865
X
z
Z-SCORES 44
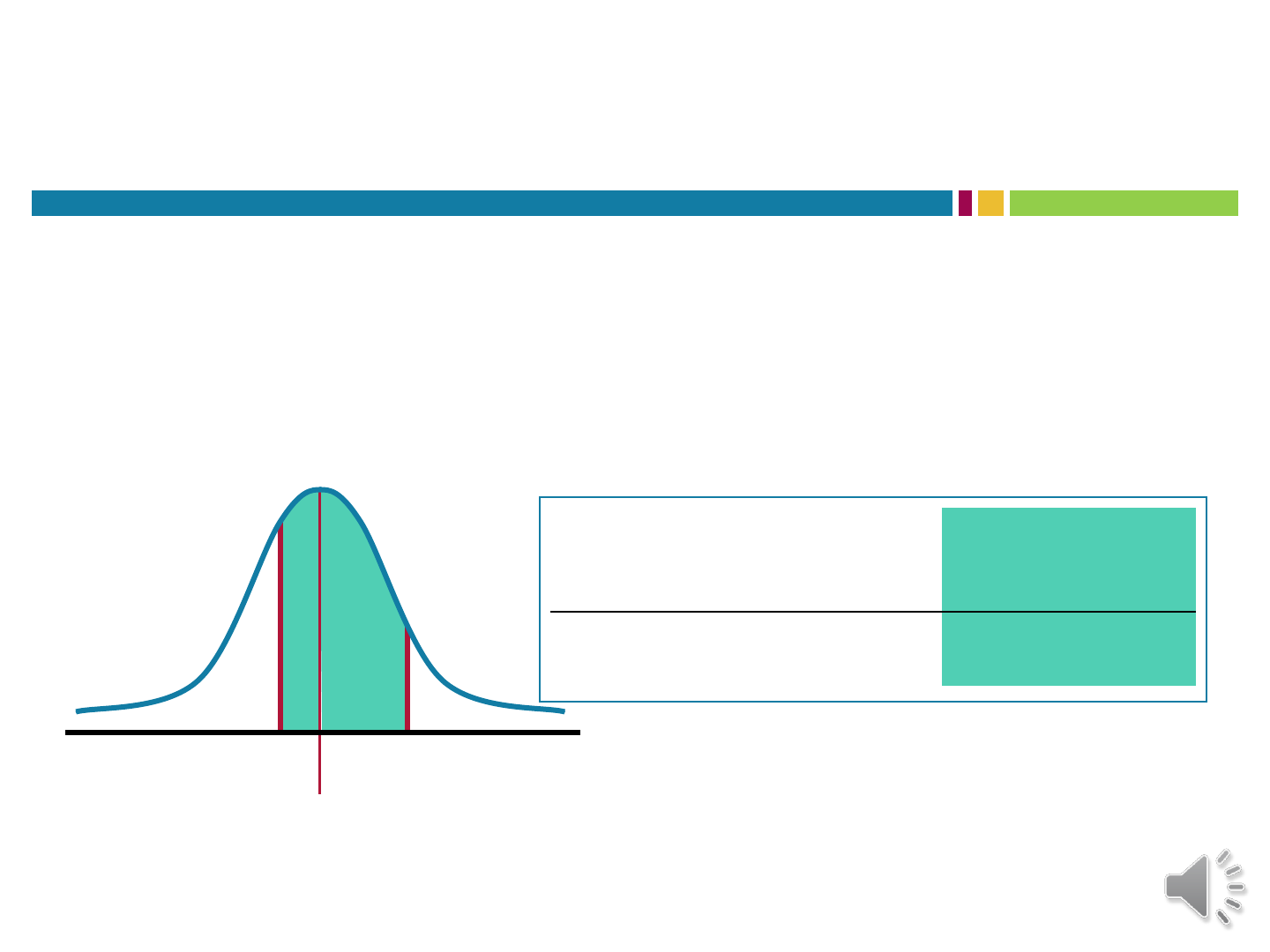
PROPORTION/PROBABILITY FOR X
Example (continued)
Step 2: Use Unit Normal Table to convert z-scores to corresponding
proportions
z = -.30 z = .70
(A)
(B) (C) (D)
z
Proportion
in Body
Proportion
in Tail
Mean and z
0.30
0.6179 0.3821 0.1179
0.70
0.758 0.242 0.2580
0, μ = 58
z
.70
Answer:
p(55 < X < 65) = p(-.30 < z < +.70) = 0.1179
+ 0.2580 = 0.3759
X=65
-.30
X=55
Z-SCORES 45
PROPORTION/PROBABILITY FOR X
Example
Assume a normal distribution with μ = 58 and σ = 10 for average speed of
cars on a section of interstate highway
What proportion of cars traveled between 65 and 75 miles per hour?
p(65 < X < 75) = ?
Step 1: Convert X values to z-Scores
70.
10
7
10
5865
X
z
70.1
10
17
10
5875
X
z
Z-SCORES 46
PROPORTION/PROBABILITY FOR X
Example (continued)
Step 2: Use Unit Normal Table to convert z-scores to corresponding
proportions
z = .70 z = 1.70
(A)
(B) (C) (D)
z
Proportion
in Body
Proportion
in Tail
Mean and z
0.70
0.758 0.242 0.2580
1.70
0.9554 0.0446 0.4554
z
.70
Answer:
p(65 < X < 75) = p(.70 < z < 1.70) = 0.4554
– 0.2580 = 0.1974
1.70
Z-SCORES 47
DISTRIBUTION OF SAMPLE MEANS
z-scores for distributions of sample means
Z-SCORES 48
DISTRIBUTION OF SAMPLE MEANS
Use of Distribution of Sample Means
Identify probability associated with a sample
Distribution = all possible M
s
Proportions = Probabilities
Z-SCORES 49
DISTRIBUTION OF SAMPLE MEANS
Example
Population of SAT scores forms normal distribution with μ = 500 and σ = 100.
In a sample of n = 25 students, what is the probability that the sample mean
will be greater than M = 540?
p(M > 540) = ?
Central Limit Theorem describes the distribution
o Distribution is normal because population of scores is normal
o Distribution mean is 500 because population mean is 500
o For n = 25, standard error of distribution is σ
M
= 20
Z-SCORES 50
DISTRIBUTION OF SAMPLE MEANS
Example (continued)
p(M > 540) = ?
Step 1: Calculate standard error of the distribution
Step 2: Calculate corresponding z-score
2
20
40
20
)500540()(
M
M
z
20
5
100
25
100
n
M
Z-SCORES 51
DISTRIBUTION OF SAMPLE MEANS
Example (continued)
p(M > 540) = ?
Step 3: Unit normal table to find correct value of p corresponding to shaded
area for z
p(M > 540) = .0228
Z-SCORES 52
Z-SCORE FOR SAMPLE MEANS
Where a sample is located relative to all other possible samples
Formula
Applications
Probabilities associated with specific means
Predict kinds of samples obtainable from a population
M
M
z
)(
Z-SCORES 53
Z-SCORE FOR SAMPLE MEANS
Example
Predict kinds of samples obtainable from a population
The distribution of SAT scores is normally distributed with a mean of μ = 500
and a standard deviation of σ = 100. Determine what kind of sample mean
is likely to be obtained as the average SAT score for a random sample of n =
25 students 80% of the time.
Z-SCORES 54
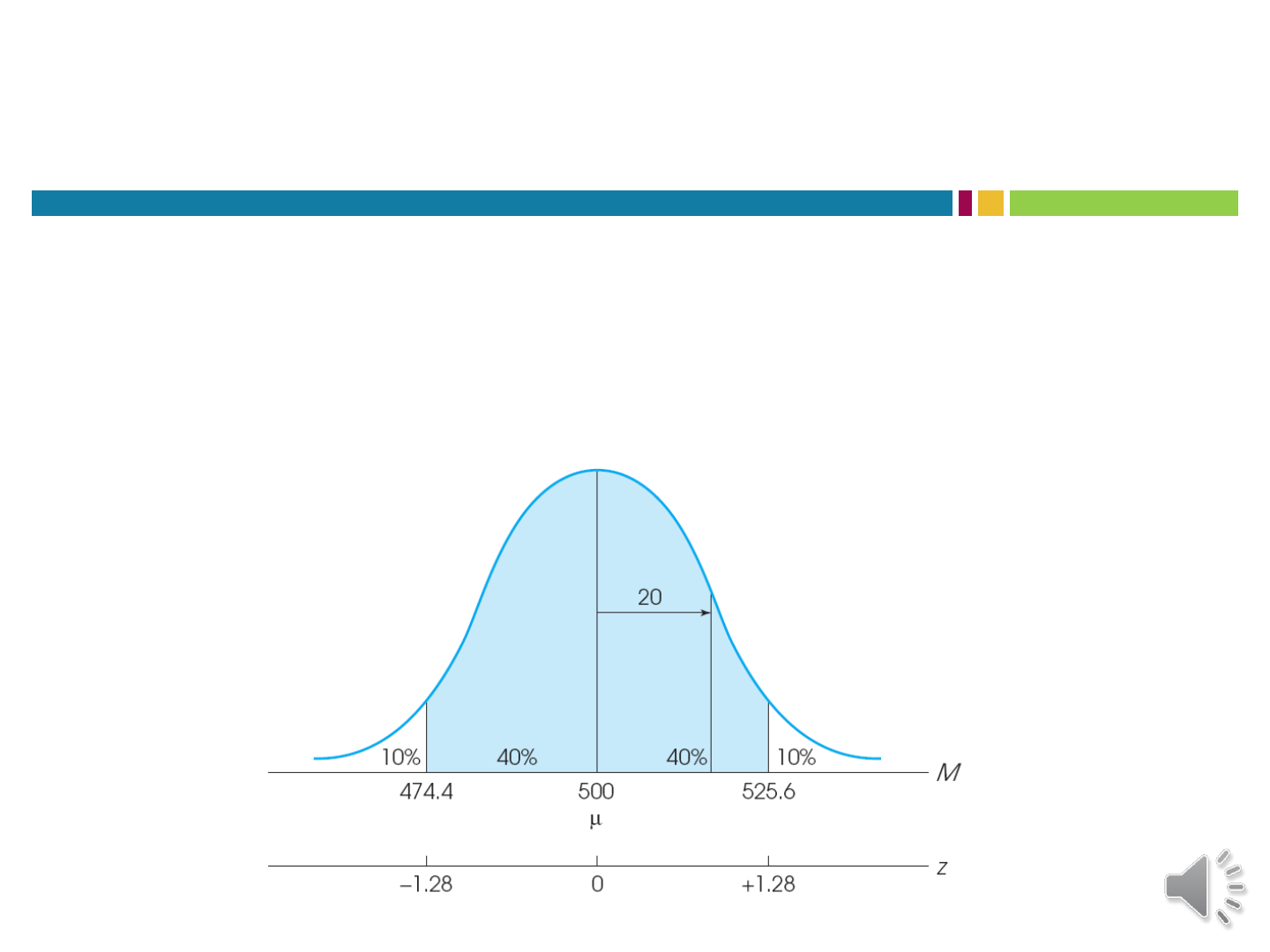
Z-SCORE FOR SAMPLE MEANS
Example (continued)
Determine what kind of sample mean is likely to be obtained as the average
SAT score for a random sample of n = 25 students 80% of the time.
Z-SCORES 55
Z-SCORE FOR SAMPLE MEANS
Example (continued)
Determine what kind of sample mean is likely to be obtained as the average
SAT score for a random sample of n = 25 students 80% of the time.
o z = -1.28 and 1.28
o Last Step: Calculate mean values
o 80% of sample means fall between 474.4 and 525.6
4.4746.25500)2028.1(500 MzM
6.5256.25500)2028.1(500 MzM
Z-SCORES 56