
HEAT CONDUCTION
EQUATION
H
eat transfer has direction as well as magnitude. The rate of heat conduc-
tion in a specified direction is proportional to the temperature gradient,
which is the rate of change in temperature with distance in that direction.
Heat conduction in a medium, in general, is three-dimensional and time depen-
dent, and the temperature in a medium varies with position as well as time, that
is, T T(x, y, z, t). Heat conduction in a medium is said to be steady when the
temperature does not vary with time, and unsteady or transient when it does.
Heat conduction in a medium is said to be one-dimensional when conduction is
significant in one dimension only and negligible in the other two primary di-
mensions, two-dimensional when conduction in the third dimension is negligi-
ble, and three-dimensional when conduction in all dimensions is significant.
We start this chapter with a description of steady, unsteady, and multidimen-
sional heat conduction. Then we derive the differential equation that governs
heat conduction in a large plane wall, a long cylinder, and a sphere, and gener-
alize the results to three-dimensional cases in rectangular, cylindrical, and spher-
ical coordinates. Following a discussion of the boundary conditions, we present
the formulation of heat conduction problems and their solutions. Finally, we
consider heat conduction problems with variable thermal conductivity.
This chapter deals with the theoretical and mathematical aspects of heat
conduction, and it can be covered selectively, if desired, without causing a sig-
nificant loss in continuity. The more practical aspects of heat conduction are
covered in the following two chapters.
63
CHAPTER
2
OBJECTIVES
When you finish studying this chapter,
you should be able to:
■ Understand multidimensionality
and time dependence of heat
transfer, and the conditions under
which a heat transfer problem
can be approximated as being
one-dimensional,
■ Obtain the differential equation
of heat conduction in various co-
ordinate systems, and simplify it
for steady one-dimensional case,
■ Identify the thermal conditions
on surfaces, and express them
mathematically as boundary
and initial conditions,
■ Solve one-dimensional heat
conduction problems and obtain
the temperature distributions
within a medium and the
heat flux,
■ Analyze one-dimensional heat
conduction in solids that involve
heat generation, and
■ Evaluate heat conduction in
solids with temperature-
dependent thermal conductivity.
cengel_ch02.qxd 1/5/10 10:45 AM Page 63

64
HEAT CONDUCTION EQUATION
2–1 INTRODUCTION
In Chapter 1 heat conduction was defined as the transfer of thermal energy
from the more energetic particles of a medium to the adjacent less energetic
ones. It was stated that conduction can take place in liquids and gases as well
as solids provided that there is no bulk motion involved.
Although heat transfer and temperature are closely related, they are of a dif-
ferent nature. Unlike temperature, heat transfer has direction as well as mag-
nitude, and thus it is a vector quantity (Fig. 2–1). Therefore, we must specify
both direction and magnitude in order to describe heat transfer completely at
a point. For example, saying that the temperature on the inner surface of a wall
is 18°C describes the temperature at that location fully. But saying that the
heat flux on that surface is 50 W/m
2
immediately prompts the question “in
what direction?” We can answer this question by saying that heat conduction
is toward the inside (indicating heat gain) or toward the outside (indicating
heat loss).
To avoid such questions, we can work with a coordinate system and indicate
direction with plus or minus signs. The generally accepted convention is that
heat transfer in the positive direction of a coordinate axis is positive and in the
opposite direction it is negative. Therefore, a positive quantity indicates heat
transfer in the positive direction and a negative quantity indicates heat trans-
fer in the negative direction (Fig. 2–2).
The driving force for any form of heat transfer is the temperature difference,
and the larger the temperature difference, the larger the rate of heat transfer.
Some heat transfer problems in engineering require the determination of the
temperature distribution (the variation of temperature) throughout the medium
in order to calculate some quantities of interest such as the local heat transfer
rate, thermal expansion, and thermal stress at some critical locations at speci-
fied times. The specification of the temperature at a point in a medium first re-
quires the specification of the location of that point. This can be done by
choosing a suitable coordinate system such as the rectangular, cylindrical, or
spherical coordinates, depending on the geometry involved, and a convenient
reference point (the origin).
The location of a point is specified as (x, y, z) in rectangular coordinates, as
(r, f, z) in cylindrical coordinates, and as (r, f, u) in spherical coordinates,
where the distances x, y, z, and r and the angles f and u are as shown in
Fig. 2–3. Then the temperature at a point (x, y, z) at time t in rectangular coor-
dinates is expressed as T(x, y, z, t). The best coordinate system for a given
geometry is the one that describes the surfaces of the geometry best. For
example, a parallelepiped is best described in rectangular coordinates
since each surface can be described by a constant value of the x-, y-, or
z-coordinates. A cylinder is best suited for cylindrical coordinates since its
lateral surface can be described by a constant value of the radius. Similarly,
the entire outer surface of a spherical body can best be described by a con-
stant value of the radius in spherical coordinates. For an arbitrarily shaped
body, we normally use rectangular coordinates since it is easier to deal with
distances than with angles.
The notation just described is also used to identify the variables involved
in a heat transfer problem. For example, the notation T(x, y, z, t) implies that
the temperature varies with the space variables x, y, and z as well as time.
■
Magnitude of
temperature
at a point A
(no direction)
Hot
baked
potato
50°C
80 W/m
2
A
Magnitude and
direction of heat
flux at the same
point
FIGURE 2–1
Heat transfer has direction as well
as magnitude, and thus it is
a vector quantity.
Cold
medium
0 L
x
Hot
medium
Q = 500 W
·
Hot
medium
0 L
x
Cold
medium
Q = –500 W
·
FIGURE 2–2
Indicating direction for heat transfer
(positive in the positive direction;
negative in the negative direction).
cengel_ch02.qxd 1/5/10 10:45 AM Page 64

65
CHAPTER 2
The notation T(x), on the other hand, indicates that the temperature varies in
the x-direction only and there is no variation with the other two space coordi-
nates or time.
Steady versus Transient Heat Transfer
Heat transfer problems are often classified as being steady (also called steady-
state) or transient (also called unsteady). The term steady implies no change
with time at any point within the medium, while transient implies variation
with time or time dependence. Therefore, the temperature or heat flux remains
unchanged with time during steady heat transfer through a medium at any
location, although both quantities may vary from one location to another
(Fig. 2–4). For example, heat transfer through the walls of a house is steady
when the conditions inside the house and the outdoors remain constant for
several hours. But even in this case, the temperatures on the inner and outer
surfaces of the wall will be different unless the temperatures inside and out-
side the house are the same. The cooling of an apple in a refrigerator, on the
other hand, is a transient heat transfer process since the temperature at any
fixed point within the apple will change with time during cooling. During
transient heat transfer, the temperature normally varies with time as well as
position. In the special case of variation with time but not with position, the
temperature of the medium changes uniformly with time. Such heat transfer
systems are called lumped systems. A small metal object such as a thermo-
couple junction or a thin copper wire, for example, can be analyzed as a
lumped system during a heating or cooling process.
Most heat transfer problems encountered in practice are transient in nature,
but they are usually analyzed under some presumed steady conditions since
steady processes are easier to analyze, and they provide the answers to our
questions. For example, heat transfer through the walls and ceiling of a typi-
cal house is never steady since the outdoor conditions such as the temperature,
the speed and direction of the wind, the location of the sun, and so on, change
constantly. The conditions in a typical house are not so steady either. There-
fore, it is almost impossible to perform a heat transfer analysis of a house
accurately. But then, do we really need an in-depth heat transfer analysis?
z
z
z
x
y
z
P(x, y, z)
(a) Rectangular coordinates (b) Cylindrical coordinates (c) Spherical coordinates
y
y
r
z
y
r
x
x
φ
P(r, , z)
φ
P(r, , )
φθ
φ
θ
x
FIGURE 2–3
The various distances
and angles involved when
describing the location of a point
in different coordinate systems.
Q
1
·
7°C15°C 15°C
Time = 2 PM
(a) Steady
Q
2
= Q
1
··
7°C
Time = 5 PM
Q
1
·
7°C15°C 12°C
(b) Transient
Q
2
≠ Q
1
··
5°C
FIGURE 2–4
Transient and steady heat
conduction in a plane wall.
cengel_ch02.qxd 1/5/10 10:45 AM Page 65

If the purpose of a heat transfer analysis of a house is to determine the proper
size of a heater, which is usually the case, we need to know the maximum rate
of heat loss from the house, which is determined by considering the heat loss
from the house under worst conditions for an extended period of time, that is,
during steady operation under worst conditions. Therefore, we can get the an-
swer to our question by doing a heat transfer analysis under steady conditions.
If the heater is large enough to keep the house warm under most demanding
conditions, it is large enough for all conditions. The approach described above
is a common practice in engineering.
Multidimensional Heat Transfer
Heat transfer problems are also classified as being one-dimensional, two-
dimensional, or three-dimensional, depending on the relative magnitudes of
heat transfer rates in different directions and the level of accuracy desired. In
the most general case, heat transfer through a medium is three-dimensional.
That is, the temperature varies along all three primary directions within the
medium during the heat transfer process. The temperature distribution
throughout the medium at a specified time as well as the heat transfer rate at
any location in this general case can be described by a set of three coordinates
such as the x, y, and z in the rectangular (or Cartesian) coordinate system; the
r, f, and z in the cylindrical coordinate system; and the r, f, and u in the
spherical (or polar) coordinate system. The temperature distribution in this
case is expressed as T(x, y, z, t), T(r, f, z, t), and T(r, f, u, t) in the respective
coordinate systems.
The temperature in a medium, in some cases, varies mainly in two primary
directions, and the variation of temperature in the third direction (and thus
heat transfer in that direction) is negligible. A heat transfer problem in that
case is said to be two-dimensional. For example, the steady temperature dis-
tribution in a long bar of rectangular cross section can be expressed as T(x, y)
if the temperature variation in the z-direction (along the bar) is negligible and
there is no change with time (Fig. 2–5).
A heat transfer problem is said to be one-dimensional if the temperature in
the medium varies in one direction only and thus heat is transferred in one
direction, and the variation of temperature and thus heat transfer in other
directions are negligible or zero. For example, heat transfer through the glass
of a window can be considered to be one-dimensional since heat transfer
through the glass occurs predominantly in one direction (the direction normal
to the surface of the glass) and heat transfer in other directions (from one side
edge to the other and from the top edge to the bottom) is negligible (Fig. 2–6).
Likewise, heat transfer through a hot water pipe can be considered to be one-
dimensional since heat transfer through the pipe occurs predominantly in the
radial direction from the hot water to the ambient, and heat transfer along the
pipe and along the circumference of a cross section (z- and -directions) is
typically negligible. Heat transfer to an egg dropped into boiling water is also
nearly one-dimensional because of symmetry. Heat is transferred to the egg in
this case in the radial direction, that is, along straight lines passing through the
midpoint of the egg.
We mentioned in Chapter 1 that the rate of heat conduction through a
medium in a specified direction (say, in the x-direction) is proportional to the
temperature difference across the medium and the area normal to the direction
66
HEAT CONDUCTION EQUATION
80°C
x
z
y
70°C
65°C
80°C
70°C
65°C
80°C
T(x, y)
70°C
65°C
Q
x
·
Q
y
·
FIGURE 2–5
Two-dimensional heat transfer
in a long rectangular bar.
Negligible
heat transfer
Primary
direction of
heat transfer
Q
·
FIGURE 2–6
Heat transfer through the window
of a house can be taken to be
one-dimensional.
cengel_ch02.qxd 1/5/10 10:45 AM Page 66

of heat transfer, but is inversely proportional to the distance in that direction.
This was expressed in the differential form by Fourier’s law of heat conduc-
tion for one-dimensional heat conduction as
Q
·
cond
kA (W) (2–1)
where k is the thermal conductivity of the material, which is a measure of the
ability of a material to conduct heat, and dT/dx is the temperature gradient,
which is the slope of the temperature curve on a T-x diagram (Fig. 2–7). The
thermal conductivity of a material, in general, varies with temperature. But
sufficiently accurate results can be obtained by using a constant value for
thermal conductivity at the average temperature.
Heat is conducted in the direction of decreasing temperature, and thus
the temperature gradient is negative when heat is conducted in the positive
x-direction. The negative sign in Eq. 2–1 ensures that heat transfer in the pos-
itive x-direction is a positive quantity.
To obtain a general relation for Fourier’s law of heat conduction, consider a
medium in which the temperature distribution is three-dimensional. Fig. 2–8
shows an isothermal surface in that medium. The heat transfer vector at a
point P on this surface must be perpendicular to the surface, and it must point
in the direction of decreasing temperature. If n is the normal of the isothermal
surface at point P, the rate of heat conduction at that point can be expressed by
Fourier’s law as
Q
·
n
kA (W) (2–2)
In rectangular coordinates, the heat conduction vector can be expressed in
terms of its components as
→
Q
·
n
Q
·
x
i
→
Q
·
y
j
→
Q
·
z
k
→
(2–3)
where i
→
, j
→
, and k
→
are the unit vectors, and Q
·
x
, Q
·
y
, and Q
·
z
are the magnitudes
of the heat transfer rates in the x-, y-, and z-directions, which again can be
determined from Fourier’s law as
Q
·
x
kA
x
, Q
·
y
kA
y
, and Q
·
z
kA
z
(2–4)
Here A
x
, A
y
and A
z
are heat conduction areas normal to the x-, y-, and
z-directions, respectively (Fig. 2–8).
Most engineering materials are isotropic in nature, and thus they have the
same properties in all directions. For such materials we do not need to be con-
cerned about the variation of properties with direction. But in anisotropic ma-
terials such as the fibrous or composite materials, the properties may change
with direction. For example, some of the properties of wood along the grain
are different than those in the direction normal to the grain. In such cases the
thermal conductivity may need to be expressed as a tensor quantity to account
for the variation with direction. The treatment of such advanced topics is be-
yond the scope of this text, and we will assume the thermal conductivity of a
material to be independent of direction.
T
z
T
y
T
x
T
n
dT
dx
67
CHAPTER 2
T
x
Q > 0
·
slope < 0
dT
—
dx
T(x)
Heat flow
FIGURE 2–7
The temperature gradient dT/dx is
simply the slope of the temperature
curve on a T-x diagram.
z
x
y
n
Q
x
·
Q
z
·
Q
n
·
Q
y
·
A
x
An isotherm
A
z
A
y
P
FIGURE 2–8
The heat transfer vector is always
normal to an isothermal surface and
can be resolved into its components
like any other vector.
cengel_ch02.qxd 1/5/10 10:45 AM Page 67

Heat Generation
A medium through which heat is conducted may involve the conversion of
mechanical, electrical, nuclear, or chemical energy into heat (or thermal en-
ergy). In heat conduction analysis, such conversion processes are character-
ized as heat (or thermal energy) generation.
For example, the temperature of a resistance wire rises rapidly when elec-
tric current passes through it as a result of the electrical energy being con-
verted to heat at a rate of I
2
R, where I is the current and R is the electrical
resistance of the wire (Fig. 2–9). The safe and effective removal of this heat
away from the sites of heat generation (the electronic circuits) is the subject
of electronics cooling, which is one of the modern application areas of heat
transfer.
Likewise, a large amount of heat is generated in the fuel elements of nuclear
reactors as a result of nuclear fission that serves as the heat source for the nu-
clear power plants. The natural disintegration of radioactive elements in nu-
clear waste or other radioactive material also results in the generation of heat
throughout the body. The heat generated in the sun as a result of the fusion of
hydrogen into helium makes the sun a large nuclear reactor that supplies heat
to the earth.
Another source of heat generation in a medium is exothermic chemical re-
actions that may occur throughout the medium. The chemical reaction in this
case serves as a heat source for the medium. In the case of endothermic reac-
tions, however, heat is absorbed instead of being released during reaction, and
thus the chemical reaction serves as a heat sink. The heat generation term be-
comes a negative quantity in this case.
Often it is also convenient to model the absorption of radiation such as so-
lar energy or gamma rays as heat generation when these rays penetrate deep
into the body while being absorbed gradually. For example, the absorption of
solar energy in large bodies of water can be treated as heat generation
throughout the water at a rate equal to the rate of absorption, which varies with
depth (Fig. 2–10). But the absorption of solar energy by an opaque body
occurs within a few microns of the surface, and the solar energy that pene-
trates into the medium in this case can be treated as specified heat flux on the
surface.
Note that heat generation is a volumetric phenomenon. That is, it occurs
throughout the body of a medium. Therefore, the rate of heat generation in a
medium is usually specified per unit volume and is denoted by e
·
gen
, whose unit
is W/m
3
or Btu/h·ft
3
.
The rate of heat generation in a medium may vary with time as well as po-
sition within the medium. When the variation of heat generation with position
is known, the total rate of heat generation in a medium of volume
V
can be de-
termined from
E
·
gen
e
·
gen
d
V
(W) (2–5)
In the special case of uniform heat generation, as in the case of electric
resistance heating throughout a homogeneous material, the relation in Eq. 2–5
reduces to E
·
gen
e
·
gen
V
, where e
·
gen
is the constant rate of heat generation per
unit volume.
冮
V
68
HEAT CONDUCTION EQUATION
FIGURE 2–9
Heat is generated in the heating coils
of an electric range as a result of the
conversion of electrical energy to heat.
Water
Solar
radiation
Solar energy
absorbed by
water
x
e
gen
(x) = q
s, absorbed
(x)
··
q
s
·
Sun
FIGURE 2–10
The absorption of solar radiation
by water can be treated as heat
generation.
cengel_ch02.qxd 1/5/10 10:45 AM Page 68

2–2 ONE-DIMENSIONAL
HEAT CONDUCTION EQUATION
Consider heat conduction through a large plane wall such as the wall of a
house, the glass of a single pane window, the metal plate at the bottom of a
pressing iron, a cast-iron steam pipe, a cylindrical nuclear fuel element, an
electrical resistance wire, the wall of a spherical container, or a spherical
metal ball that is being quenched or tempered. Heat conduction in these
and many other geometries can be approximated as being one-dimensional
since heat conduction through these geometries is dominant in one
direction and negligible in other directions. Next we develop the one-
dimensional heat conduction equation in rectangular, cylindrical, and spher-
ical coordinates.
Heat Conduction Equation in a Large Plane Wall
Consider a thin element of thickness x in a large plane wall, as shown in
Fig. 2–12. Assume the density of the wall is r, the specific heat is c, and the
area of the wall normal to the direction of heat transfer is A. An energy bal-
ance on this thin element during a small time interval t can be expressed as
■
69
CHAPTER 2
EXAMPLE 2–1
Heat Generation in a Hair Dryer
The resistance wire of a 1200-W hair dryer is 80 cm long and has a diameter
of
D
0.3 cm (Fig. 2–11). Determine the rate of heat generation in the wire
per unit volume, in W/cm
3
, and the heat flux on the outer surface of the wire
as a result of this heat generation.
SOLUTION The power consumed by the resistance wire of a hair dryer is
given. The heat generation and the heat flux are to be determined.
Assumptions
Heat is generated uniformly in the resistance wire.
Analysis
A 1200-W hair dryer converts electrical energy into heat in the wire
at a rate of 1200 W. Therefore, the rate of heat generation in a resistance wire
is equal to the power consumption of a resistance heater. Then the rate of heat
generation in the wire per unit volume is determined by dividing the total rate
of heat generation by the volume of the wire,
e
·
gen
212 W/cm
3
Similarly, heat flux on the outer surface of the wire as a result of this heat gen-
eration is determined by dividing the total rate of heat generation by the
surface area of the wire,
Q
·
s
15.9 W/cm
3
Discussion
Note that heat generation is expressed per unit volume in W/cm
3
or Btu/h·ft
3
, whereas heat flux is expressed per unit surface area in W/cm
2
or
Btu/h·ft
2
.
1200 W
p(0.3 cm)(80 cm)
E
.
gen
pDL
E
.
gen
A
wire
1200 W
[p(0.3 cm)
2
/4](80 cm)
E
.
gen
(pD
2
/4)L
E
.
gen
V
wire
Hair dryer
1200 W
FIGURE 2–11
Schematic for Example 2–1.
0
Vo l ume
element
A
x
A
x
= A
x + Δx
= A
L
x
x + Δx
Q
x
·
Q
x + Δx
·
E
gen
·
FIGURE 2–12
One-dimensional heat conduction
through a volume element in
a large plane wall.
cengel_ch02.qxd 1/5/10 10:45 AM Page 69

or
Q
·
x
Q
·
x x
E
·
gen, element
(2–6)
But the change in the energy content of the element and the rate of heat gen-
eration within the element can be expressed as
E
element
E
t t
E
t
mc(T
t t
T
t
) rcAx(T
t t
T
t
) (2–7)
E
·
gen, element
e
·
gen
V
element
e
·
gen
Ax (2–8)
Substituting into Eq. 2–6, we get
Q
·
x
Q
·
x x
e
·
gen
Ax rcAx (2–9)
Dividing by Axgives
e
·
gen
rc (2–10)
Taking the limit as x → 0 and t → 0 yields
e
·
gen
rc (2–11)
since, from the definition of the derivative and Fourier’s law of heat
conduction,
(2–12)
Noting that the area A is constant for a plane wall, the one-dimensional tran-
sient heat conduction equation in a plane wall becomes
Variable conductivity: e
·
gen
rc (2–13)
The thermal conductivity k of a material, in general, depends on the tempera-
ture T (and therefore x), and thus it cannot be taken out of the derivative. How-
ever, the thermal conductivity in most practical applications can be assumed to
remain constant at some average value. The equation above in that case
reduces to
Constant conductivity: (2–14)
where the property a k/rc is the thermal diffusivity of the material and
represents how fast heat propagates through a material. It reduces to the
following forms under specified conditions (Fig. 2–13):
T
t
1
a
e
.
gen
k
2
T
x
2
T
t
冢
k
T
x
冣
x
冢
kA
T
x
冣
x
Q
x
Q
x x
Q
x
x
lim
x → 0
T
t
冢
kA
T
x
冣
x
1
A
T
t t
T
t
t
Q
.
xx
Q
.
x
x
1
A
T
t t
T
t
t
E
element
t
冢
Rate of change
of the energy
content of the
element
冣冢
Rate of heat
generation
inside the
element
冣
冢
Rate of heat
conduction
at x x
冣冢
Rate of heat
conduction
at x
冣
70
HEAT CONDUCTION EQUATION
FIGURE 2–13
The simplification of the one-
dimensional heat conduction equation
in a plane wall for the case of constant
conductivity for steady conduction
with no heat generation.
General, one-dimensional:
Steady, one-dimensional:
No
generation
Steady-
state
∂
2
T
∂x
2
d
2
T
dx
2
e
gen
k
1
a
∂T
∂t
+=
= 0
00
·
cengel_ch02.qxd 1/5/10 10:45 AM Page 70

0 (2–15)
(2–16)
0 (2–17)
Note that we replaced the partial derivatives by ordinary derivatives in the
one-dimensional steady heat conduction case since the partial and ordinary
derivatives of a function are identical when the function depends on a single
variable only [T T(x) in this case].
Heat Conduction Equation in a Long Cylinder
Now consider a thin cylindrical shell element of thickness r in a long
cylinder, as shown in Fig. 2–14. Assume the density of the cylinder is r,the
specific heat is c, and the length is L. The area of the cylinder normal to the
direction of heat transfer at any location is A 2prL where r is the value of
the radius at that location. Note that the heat transfer area A depends on r
in this case, and thus it varies with location. An energy balance on this thin
cylindrical shell element during a small time interval t can be expressed as
or
Q
·
r
Q
·
r r
E
·
gen, element
(2–18)
The change in the energy content of the element and the rate of heat genera-
tion within the element can be expressed as
E
element
E
t t
E
t
mc(T
t t
T
t
) rcAr(T
t t
T
t
) (2–19)
E
·
gen, element
e
·
gen
V
element
e
·
gen
Ar (2–20)
Substituting into Eq. 2–18, we get
Q
·
r
Q
·
r r
e
·
gen
Ar rcAr (2–21)
where A 2prL. You may be tempted to express the area at the middle of
the element using the average radius as A 2p(r r/2)L. But there is
nothing we can gain from this complication since later in the analysis we
will take the limit as r
→ 0 and thus the term r/2 will drop out. Now
dividing the equation above by Ar gives
e
·
gen
rc (2–22)
Taking the limit as r → 0 and t → 0 yields
e
·
gen
rc (2–23)
T
t
冢
kA
T
r
冣
r
1
A
T
t t
T
t
t
Q
.
r r
Q
.
r
r
1
A
T
t t
T
t
t
E
element
t
冢
Rate of change
of the energy
content of the
element
冣冢
Rate of heat
generation
inside the
element
冣
冢
Rate of heat
conduction
at r r
冣冢
Rate of heat
conduction
at r
冣
d
2
T
dx
2
(3) Steady-state, no heat generation:
(/t 0 and e
·
gen
0)
T
t
1
a
2
T
x
2
(2) Transient, no heat generation:
(e
·
gen
0)
e
.
gen
k
d
2
T
dx
2
(1) Steady-state:
(/t 0)
71
CHAPTER 2
L
0
Volume element
r + Δr
r
r
Q
r
·
Q
r + Δr
·
E
gen
·
FIGURE 2–14
One-dimensional heat conduction
through a volume element
in a long cylinder.
cengel_ch02.qxd 1/5/10 10:45 AM Page 71

since, from the definition of the derivative and Fourier’s law of heat conduction,
(2–24)
Noting that the heat transfer area in this case is A = 2prL, the one-dimensional
transient heat conduction equation in a cylinder becomes
Variable conductivity: e
·
gen
rc (2–25)
For the case of constant thermal conductivity, the previous equation reduces to
Constant conductivity: (2–26)
where again the property a k/rc is the thermal diffusivity of the mate-
rial. Eq. 2–26 reduces to the following forms under specified conditions
(Fig. 2–15):
0 (2–27)
(2–28)
0 (2–29)
Note that we again replaced the partial derivatives by ordinary derivatives in
the one-dimensional steady heat conduction case since the partial and ordinary
derivatives of a function are identical when the function depends on a single
variable only [T T(r) in this case].
Heat Conduction Equation in a Sphere
Now consider a sphere with density , specific heat c, and outer radius R. The
area of the sphere normal to the direction of heat transfer at any location is
A 4pr
2
, where r is the value of the radius at that location. Note that the heat
transfer area A depends on r in this case also, and thus it varies with location.
By considering a thin spherical shell element of thickness r and repeating
the approach described above for the cylinder by using A 4pr
2
instead of
A 2prL, the one-dimensional transient heat conduction equation for a
sphere is determined to be (Fig. 2–16)
Variable conductivity: e
·
gen
rc (2–30)
which, in the case of constant thermal conductivity, reduces to
Constant conductivity: (2–31)
where again the property a k/rc is the thermal diffusivity of the material. It
reduces to the following forms under specified conditions:
T
t
1
a
e
.
gen
k
冢
r
2
T
r
冣
r
1
r
2
T
t
冢
r
2
k
T
r
冣
r
1
r
2
冢
r
dT
dr
冣
d
dr
(3) Steady-state, no heat generation:
(/t 0 and e
·
gen
0)
T
t
1
冢
r
T
r
冣
r
1
r
(2) Transient, no heat generation:
(e
·
gen
0)
e
.
gen
k
冢
r
dT
dr
冣
d
dr
1
r
(1) Steady-state:
(/t 0)
T
t
1
a
e
.
gen
k
冢
r
T
r
冣
r
1
r
T
t
冢
rk
T
r
冣
r
1
r
冢
kA
T
r
冣
r
Q
.
r
Q
.
rr
Q
.
r
r
lim
r → 0
72
HEAT CONDUCTION EQUATION
FIGURE 2–15
Two equivalent forms of the
differential equation for the one-
dimensional steady heat conduction in
a cylinder with no heat generation.
0
R
Vo l ume
element
r + Δr
rr
Q
r
·
Q
r + Δr
·
E
gen
·
FIGURE 2–16
One-dimensional heat conduction
through a volume element in a sphere.
(a) The form that is ready to integrate
(b) The equivalent alternative form
d
dr
dT
dr
r
= 0
d
2
T
dr
2
dT
dr
r
= 0
+
cengel_ch02.qxd 1/5/10 10:45 AM Page 72

0 (2–32)
(2–33)
0orr 2 0 (2–34)
where again we replaced the partial derivatives by ordinary derivatives in the
one-dimensional steady heat conduction case.
Combined One-Dimensional
Heat Conduction Equation
An examination of the one-dimensional transient heat conduction equations
for the plane wall, cylinder, and sphere reveals that all three equations can be
expressed in a compact form as
e
·
gen
rc (2–35)
where n 0 for a plane wall, n 1 for a cylinder, and n 2 for a sphere. In
the case of a plane wall, it is customary to replace the variable r by x. This
equation can be simplified for steady-state or no heat generation cases as
described before.
T
t
冢
r
n
k
T
r
冣
r
1
r
n
dT
dr
d
2
T
dr
2
冢
r
2
dT
dr
冣
d
dr
(3) Steady-state,
no heat generation:
(/t 0 and e
·
gen
0)
T
t
1
a
冢
r
2
T
r
冣
r
1
r
2
(2) Transient,
no heat generation:
(e
·
gen
0)
e
.
gen
k
冢
r
2
dT
dr
冣
d
dr
1
r
2
(1) Steady-state:
(/t 0)
73
CHAPTER 2
EXAMPLE 2–2
Heat Conduction through the Bottom of a Pan
Consider a steel pan placed on top of an electric range to cook spaghetti
(Fig. 2–17). The bottom section of the pan is 0.4 cm thick and has a diameter
of 18 cm. The electric heating unit on the range top consumes 800 W of power
during cooking, and 80 percent of the heat generated in the heating element
is transferred uniformly to the pan. Assuming constant thermal conductivity,
obtain the differential equation that describes the variation of the temperature
in the bottom section of the pan during steady operation.
SOLUTION A steel pan placed on top of an electric range is considered. The
differential equation for the variation of temperature in the bottom of the pan
is to be obtained.
Analysis
The bottom section of the pan has a large surface area relative to its
thickness and can be approximated as a large plane wall. Heat flux is applied to
the bottom surface of the pan uniformly, and the conditions on the inner surface
are also uniform. Therefore, we expect the heat transfer through the bottom sec-
tion of the pan to be from the bottom surface toward the top, and heat transfer
in this case can reasonably be approximated as being one-dimensional. Taking
the direction normal to the bottom surface of the pan to be the
x
-axis, we will
have
T
T
(
x
) during steady operation since the temperature in this case will
depend on
x
only.
800 W
FIGURE 2–17
Schematic for Example 2–2.
cengel_ch02.qxd 1/5/10 10:45 AM Page 73

74
HEAT CONDUCTION EQUATION
The thermal conductivity is given to be constant, and there is no heat gener-
ation in the medium (within the bottom section of the pan). Therefore, the dif-
ferential equation governing the variation of temperature in the bottom section
of the pan in this case is simply Eq. 2–17,
0
which is the steady one-dimensional heat conduction equation in rectangular
coordinates under the conditions of constant thermal conductivity and no heat
generation.
Discussion
Note that the conditions at the surface of the medium have no ef-
fect on the differential equation.
d
2
T
dx
2
EXAMPLE 2–3
Heat Conduction in a Resistance Heater
A 2-kW resistance heater wire with thermal conductivity
k
15 W/m·K, diam-
eter
D
0.4 cm, and length
L
50 cm is used to boil water by immersing
it in water (Fig. 2–18). Assuming the variation of the thermal conductivity of
the wire with temperature to be negligible, obtain the differential equation that
describes the variation of the temperature in the wire during steady operation.
SOLUTION The resistance wire of a water heater is considered. The differen-
tial equation for the variation of temperature in the wire is to be obtained.
Analysis
The resistance wire can be considered to be a very long cylinder since
its length is more than 100 times its diameter. Also, heat is generated uniformly
in the wire and the conditions on the outer surface of the wire are uniform.
Therefore, it is reasonable to expect the temperature in the wire to vary in the
radial
r
direction only and thus the heat transfer to be one-dimensional. Then
we have
T
T
(
r
) during steady operation since the temperature in this case de-
pends on
r
only.
The rate of heat generation in the wire per unit volume can be determined
from
e
·
gen
0.318 10
9
W/m
3
Noting that the thermal conductivity is given to be constant, the differential
equation that governs the variation of temperature in the wire is simply
Eq. 2–27,
0
which is the steady one-dimensional heat conduction equation in cylindrical
coordinates for the case of constant thermal conductivity.
Discussion
Note again that the conditions at the surface of the wire have no
effect on the differential equation.
e
.
gen
k
ar
dT
dr
b
d
dr
1
r
2000 W
[p(0.004 m)
2
/4](0.5 m)
E
.
gen
(pD
2
/4)L
E
.
gen
V
wire
Water
Resistance
heater
FIGURE 2–18
Schematic for Example 2–3.
cengel_ch02.qxd 1/5/10 10:46 AM Page 74

2–3 GENERAL HEAT CONDUCTION EQUATION
In the last section we considered one-dimensional heat conduction and
assumed heat conduction in other directions to be negligible. Most heat trans-
fer problems encountered in practice can be approximated as being one-
dimensional, and we mostly deal with such problems in this text. However,
this is not always the case, and sometimes we need to consider heat transfer in
other directions as well. In such cases heat conduction is said to be multidi-
mensional, and in this section we develop the governing differential equation
in such systems in rectangular, cylindrical, and spherical coordinate systems.
Rectangular Coordinates
Consider a small rectangular element of length x, width y, and height z,
as shown in Fig. 2–20. Assume the density of the body is r and the specific
heat is c. An energy balance on this element during a small time interval t
can be expressed as
冢
Rate of change
of the energy
content of
the element
冣冢
Rate of heat
generation
inside the
element
冣冢
Rate of heat
conduction
at x x,
y y, and z z
冣
冢
Rate of heat
conduction at
x, y, and z
冣
■
75
CHAPTER 2
EXAMPLE 2–4
Cooling of a Hot Metal Ball in Air
A spherical metal ball of radius
R
is heated in an oven to a temperature of
600°F throughout and is then taken out of the oven and allowed to cool in am-
bient air at
T
75°F by convection and radiation (Fig. 2–19). The thermal
conductivity of the ball material is known to vary linearly with temperature. As-
suming the ball is cooled uniformly from the entire outer surface, obtain the
differential equation that describes the variation of the temperature in the ball
during cooling.
SOLUTION A hot metal ball is allowed to cool in ambient air. The differential
equation for the variation of temperature within the ball is to be obtained.
Analysis
The ball is initially at a uniform temperature and is cooled uniformly
from the entire outer surface. Also, the temperature at any point in the ball
changes with time during cooling. Therefore, this is a one-dimensional tran-
sient heat conduction problem since the temperature within the ball changes
with the radial distance
r
and the time
t
. That is,
T
T
(
r, t
).
The thermal conductivity is given to be variable, and there is no heat gener-
ation in the ball. Therefore, the differential equation that governs the variation
of temperature in the ball in this case is obtained from Eq. 2–30 by setting the
heat generation term equal to zero. We obtain
rc
which is the one-dimensional transient heat conduction equation in spherical
coordinates under the conditions of variable thermal conductivity and no heat
generation.
Discussion
Note again that the conditions at the outer surface of the ball have
no effect on the differential equation.
T
t
ar
2
k
T
r
b
r
1
r
2
Metal ball
600°F
75°F
Q
·
FIGURE 2–19
Schematic for Example 2–4.
Q
x
·
Q
z + Δz
·
Q
y + Δy
·
Q
x + Δ
x
·
Q
y
·
Q
z
·
Δx
Δy
Δz
x
z
y
Volume element
e
gen
ΔxΔyΔz
·
FIGURE 2–20
Three-dimensional heat conduction
through a rectangular volume element.
cengel_ch02.qxd 1/5/10 10:46 AM Page 75

or
Q
·
x
Q
·
y
Q
·
z
Q
·
x x
Q
·
y y
Q
·
z z
E
·
gen, element
(2–36)
Noting that the volume of the element is
V
element
xyz, the change in the
energy content of the element and the rate of heat generation within the ele-
ment can be expressed as
E
element
E
t t
E
t
mc(T
t t
T
t
) rcxyz(T
t t
T
t
)
E
·
gen, element
e
·
gen
V
element
e
·
gen
xyz
Substituting into Eq. 2–36, we get
Q
·
x
Q
·
y
Q
·
z
Q
·
x x
Q
·
y y
Q
·
z z
e
·
gen
xyz rcxyz
Dividing by xyz gives
e
·
gen
rc
(2–37)
Noting that the heat transfer areas of the element for heat conduction in the
x, y, and z directions are A
x
yz, A
y
xz, and A
z
xy, respectively,
and taking the limit as x, y, z and t
→ 0 yields
e
·
gen
rc (2–38)
since, from the definition of the derivative and Fourier’s law of heat
conduction,
Eq. 2–38 is the general heat conduction equation in rectangular coordinates.
In the case of constant thermal conductivity, it reduces to
(2–39)
where the property a k/rc is again the thermal diffusivity of the material.
Eq. 2–39 is known as the Fourier-Biot equation, and it reduces to these
forms under specified conditions:
T
t
1
a
e
.
gen
k
2
T
z
2
2
T
y
2
2
T
x
2
冢
k
T
z
冣
z
冢
kxy
T
z
冣
z
1
xy
Q
z
z
1
xy
Q
.
zz
Q
.
z
z
1
xy
lim
z → 0
冢
k
T
y
冣
y
冢
kxz
T
y
冣
y
1
xz
Q
y
y
1
xz
Q
.
yy
Q
.
y
y
1
xz
lim
y → 0
冢
k
T
x
冣
x
冢
kyz
T
x
冣
x
1
yz
Q
x
x
1
yz
Q
.
xx
Q
.
x
˛˛x
1
yz
lim
x → 0
T
t
冢
k
T
z
冣
z
冢
k
T
y
冣
y
冢
k
T
x
冣
x
T
tt
T
t
t
Q
.
zz
Q
.
z
z
1
xy
Q
.
yy
Q
.
y
y
1
xz
Q
.
xx
Q
.
x
x
1
yz
T
tt
T
t
t
E
element
t
76
HEAT CONDUCTION EQUATION
cengel_ch02.qxd 1/5/10 10:46 AM Page 76

0 (2–40)
(2–41)
0 (2–42)
Note that in the special case of one-dimensional heat transfer in the x-direction,
the derivatives with respect to y and z drop out and the equations above reduce
to the ones developed in the previous section for a plane wall (Fig. 2–21).
Cylindrical Coordinates
The general heat conduction equation in cylindrical coordinates can be
obtained from an energy balance on a volume element in cylindrical coor-
dinates, shown in Fig. 2–22, by following the steps just outlined. It can also
be obtained directly from Eq. 2–38 by coordinate transformation using the
following relations between the coordinates of a point in rectangular and
cylindrical coordinate systems:
x r cos f, y r sin f, and z z
After lengthy manipulations, we obtain
e
·
gen
rc (2–43)
Spherical Coordinates
The general heat conduction equations in spherical coordinates can be ob-
tained from an energy balance on a volume element in spherical coordinates,
shown in Fig. 2–23, by following the steps outlined above. It can also be ob-
tained directly from Eq. 2–38 by coordinate transformation using the follow-
ing relations between the coordinates of a point in rectangular and spherical
coordinate systems:
x r cos f sin u, y r sin f sin u, and z cos u
Again after lengthy manipulations, we obtain
e
·
gen
rc
(2–44)
Obtaining analytical solutions to these differential equations requires a
knowledge of the solution techniques of partial differential equations, which
is beyond the scope of this introductory text. Here we limit our consideration
to one-dimensional steady-state cases, since they result in ordinary differen-
tial equations.
T
t
ak sin u
T
u
b
u
1
r
2
sin u
ak
T
f
b
f
1
r
2
sin
2
u
冢
kr
2
T
r
冣
r
1
r
2
T
t
冢
k
T
z
冣
z
ak
T
f
b
T
f
1
r
2
冢
kr
T
r
冣
r
1
r
2
T
z
2
2
T
y
2
2
T
x
2
(3) Steady-state, no heat generation:
(called the Laplace equation)
T
t
1
a
2
T
z
2
2
T
y
2
2
T
x
2
(2) Transient, no heat generation:
(called the diffusion equation)
e
.
gen
k
2
T
z
2
2
T
y
2
2
T
x
2
(1) Steady-state:
(called the Poisson equation)
77
CHAPTER 2
∂
2
T
∂x
2
∂
2
T
∂y
2
e
gen
k
∂
2
T
∂x
2
∂
2
T
∂x
2
++
∂
2
T
∂z
2
+= 0
= 0
∂
2
T
∂y
2
∂T
∂t
1
a
++
∂
2
T
∂z
2
=
∂
2
T
∂y
2
++
∂
2
T
∂z
2
·
FIGURE 2–21
The three-dimensional heat
conduction equations reduce to
the one-dimensional ones when
the temperature varies in one
dimension only.
dz
dφ
φ
y
z
z
x
dr
r
FIGURE 2–22
A differential volume element in
cylindrical coordinates.
y
x
z
dr
r
θ
φ
dθ
dφ
FIGURE 2–23
A differential volume element in
spherical coordinates.
cengel_ch02.qxd 1/5/10 10:46 AM Page 77

2–4 BOUNDARY AND INITIAL CONDITIONS
The heat conduction equations above were developed using an energy balance
on a differential element inside the medium, and they remain the same re-
gardless of the thermal conditions on the surfaces of the medium. That is, the
differential equations do not incorporate any information related to the condi-
tions on the surfaces such as the surface temperature or a specified heat flux.
Yet we know that the heat flux and the temperature distribution in a medium
depend on the conditions at the surfaces, and the description of a heat transfer
problem in a medium is not complete without a full description of the thermal
conditions at the bounding surfaces of the medium. The mathematical expres-
sions of the thermal conditions at the boundaries are called the boundary
conditions.
■
78
HEAT CONDUCTION EQUATION
EXAMPLE 2–5
Heat Conduction in a Short Cylinder
A short cylindrical metal billet of radius
R
and height
h
is heated in an oven to
a temperature of 600°F throughout and is then taken out of the oven and al-
lowed to cool in ambient air at
T
65°F by convection and radiation. As-
suming the billet is cooled uniformly from all outer surfaces and the variation
of the thermal conductivity of the material with temperature is negligible, ob-
tain the differential equation that describes the variation of the temperature in
the billet during this cooling process.
SOLUTION A short cylindrical billet is cooled in ambient air. The differential
equation for the variation of temperature is to be obtained.
Analysis
The billet shown in Fig. 2–24 is initially at a uniform temperature
and is cooled uniformly from the top and bottom surfaces in the
z
-direction as
well as the lateral surface in the radial
r
-direction. Also, the temperature at any
point in the ball changes with time during cooling. Therefore, this is a two-
dimensional transient heat conduction problem since the temperature within
the billet changes with the radial and axial distances
r
and
z
and with time
t.
That is,
T
T
(
r, z, t
).
The thermal conductivity is given to be constant, and there is no heat gener-
ation in the billet. Therefore, the differential equation that governs the varia-
tion of temperature in the billet in this case is obtained from Eq. 2–43 by
setting the heat generation term and the derivatives with respect to f equal to
zero. We obtain
rc
In the case of constant thermal conductivity, it reduces to
which is the desired equation.
Discussion
Note that the boundary and initial conditions have no effect on the
differential equation.
T
t
1
a
2
T
z
2
冢
r
T
r
冣
r
1
r
T
t
ak
T
z
b
z
akr
T
r
b
r
1
r
z
600°F
T
⬁
= 65°F
Metal
billet
Heat
loss
r
R
φ
FIGURE 2–24
Schematic for Example 2–5.
cengel_ch02.qxd 1/5/10 10:46 AM Page 78

From a mathematical point of view, solving a differential equation is essen-
tially a process of removing derivatives, or an integration process, and thus the
solution of a differential equation typically involves arbitrary constants
(Fig. 2–25). It follows that to obtain a unique solution to a problem, we need
to specify more than just the governing differential equation. We need to spec-
ify some conditions (such as the value of the function or its derivatives at
some value of the independent variable) so that forcing the solution to satisfy
these conditions at specified points will result in unique values for the arbi-
trary constants and thus a unique solution. But since the differential equation
has no place for the additional information or conditions, we need to supply
them separately in the form of boundary or initial conditions.
Consider the variation of temperature along the wall of a brick house in
winter. The temperature at any point in the wall depends on, among other
things, the conditions at the two surfaces of the wall such as the air tempera-
ture of the house, the velocity and direction of the winds, and the solar energy
incident on the outer surface. That is, the temperature distribution in a medium
depends on the conditions at the boundaries of the medium as well as the heat
transfer mechanism inside the medium. To describe a heat transfer problem
completely, two boundary conditions must be given for each direction of the
coordinate system along which heat transfer is significant (Fig. 2–26). There-
fore, we need to specify two boundary conditions for one-dimensional prob-
lems, four boundary conditions for two-dimensional problems, and six
boundary conditions for three-dimensional problems. In the case of the wall
of a house, for example, we need to specify the conditions at two locations
(the inner and the outer surfaces) of the wall since heat transfer in this case is
one-dimensional. But in the case of a parallelepiped, we need to specify six
boundary conditions (one at each face) when heat transfer in all three dimen-
sions is significant.
The physical argument presented above is consistent with the mathematical
nature of the problem since the heat conduction equation is second order (i.e.,
involves second derivatives with respect to the space variables) in all directions
along which heat conduction is significant, and the general solution of a sec-
ond-order linear differential equation involves two arbitrary constants for each
direction. That is, the number of boundary conditions that needs to be specified
in a direction is equal to the order of the differential equation in that direction.
Reconsider the brick wall already discussed. The temperature at any point
on the wall at a specified time also depends on the condition of the wall at the
beginning of the heat conduction process. Such a condition, which is usually
specified at time t 0, is called the initial condition, which is a mathemati-
cal expression for the temperature distribution of the medium initially. Note
that we need only one initial condition for a heat conduction problem regard-
less of the dimension since the conduction equation is first order in time (it in-
volves the first derivative of temperature with respect to time).
In rectangular coordinates, the initial condition can be specified in the gen-
eral form as
T(x, y, z, 0) f(x, y, z) (2–45)
where the function f(x, y, z) represents the temperature distribution through-
out the medium at time t 0. When the medium is initially at a uniform
79
CHAPTER 2
d
2
T
dx
2
= 0
The differential equation:
T(x) = C
1
x + C
2
T(x) = 2x + 5
T(x) = –x + 12
T(x) = –3
T(x) = 6.2x
Arbitrary constants
Some specific solutions:
General solution:
…
FIGURE 2–25
The general solution of a typical
differential equation involves
arbitrary constants, and thus an
infinite number of solutions.
Some solutions of
= 0
d
2
T
–—
dx
2
15°C
The only solution
that satisfies
the conditions
T(0) = 50°C
and T(L) = 15°C.
50°C
0
L
x
T
FIGURE 2–26
To describe a heat transfer problem
completely, two boundary conditions
must be given for each direction along
which heat transfer is significant.
cengel_ch02.qxd 1/5/10 10:46 AM Page 79
temperature of T
i
, the initial condition in Eq. 2–45 can be expressed as T(x, y,
z, 0) T
i
. Note that under steady conditions, the heat conduction equation
does not involve any time derivatives, and thus we do not need to specify an
initial condition.
The heat conduction equation is first order in time, and thus the initial con-
dition cannot involve any derivatives (it is limited to a specified temperature).
However, the heat conduction equation is second order in space coordinates,
and thus a boundary condition may involve first derivatives at the boundaries
as well as specified values of temperature. Boundary conditions most com-
monly encountered in practice are the specified temperature, specified heat
flux, convection, and radiation boundary conditions.
1 Specified Temperature Boundary Condition
The temperature of an exposed surface can usually be measured directly and
easily. Therefore, one of the easiest ways to specify the thermal conditions on
a surface is to specify the temperature. For one-dimensional heat transfer
through a plane wall of thickness L, for example, the specified temperature
boundary conditions can be expressed as (Fig. 2–27)
T(0, t) T
1
T(L, t) T
2
(2–46)
where T
1
and T
2
are the specified temperatures at surfaces at x 0 and x L,
respectively. The specified temperatures can be constant, which is the case for
steady heat conduction, or may vary with time.
2 Specified Heat Flux Boundary Condition
When there is sufficient information about energy interactions at a surface, it
may be possible to determine the rate of heat transfer and thus the heat flux q
·
(heat transfer rate per unit surface area, W/m
2
) on that surface, and this infor-
mation can be used as one of the boundary conditions. The heat flux in the
positive x-direction anywhere in the medium, including the boundaries, can be
expressed by Fourier’s law of heat conduction as
q
·
k (W/m
2
) (2–47)
Then the boundary condition at a boundary is obtained by setting the specified
heat flux equal to k(T/x) at that boundary. The sign of the specified heat
flux is determined by inspection: positive if the heat flux is in the positive di-
rection of the coordinate axis, and negative if it is in the opposite direction.
Note that it is extremely important to have the correct sign for the specified
heat flux since the wrong sign will invert the direction of heat transfer and
cause the heat gain to be interpreted as heat loss (Fig. 2–28).
For a plate of thickness L subjected to heat flux of 50 W/m
2
into the medium
from both sides, for example, the specified heat flux boundary conditions can
be expressed as
k 50 and k 50 (2–48)
T(L, t)
x
T(0, t)
x
a
Heat flux in the
positive x direction
b
T
x
80
HEAT CONDUCTION EQUATION
0
Heat
flux Conduction
L
x
Heat
fluxConduction
q
0
= –k
∂T(0, t)
———
∂x
.
–k
= q
L
∂T(L, t)
———
∂x
.
FIGURE 2–28
Specified heat flux boundary
conditions on both surfaces
of a plane wall.
70°C150°C T(x, t)
0
L
x
T(0, t) = 150°C
T(L, t) = 70°C
FIGURE 2–27
Specified temperature boundary
conditions on both surfaces
of a plane wall.
cengel_ch02.qxd 1/5/10 10:46 AM Page 80

Note that the heat flux at the surface at x L is in the negative x-direction,
and thus it is 50 W/m
2
. The direction of heat flux arrows at x L in
Fig. 2–28 in this case would be reversed.
Special Case: Insulated Boundary
Some surfaces are commonly insulated in practice in order to minimize heat
loss (or heat gain) through them. Insulation reduces heat transfer but does not
totally eliminate it unless its thickness is infinity. However, heat transfer
through a properly insulated surface can be taken to be zero since adequate
insulation reduces heat transfer through a surface to negligible levels. There-
fore, a well-insulated surface can be modeled as a surface with a specified heat
flux of zero. Then the boundary condition on a perfectly insulated surface (at
x 0, for example) can be expressed as (Fig. 2–29)
k 0or 0 (2–49)
That is, on an insulated surface, the first derivative of temperature with re-
spect to the space variable (the temperature gradient) in the direction normal
to the insulated surface is zero. This also means that the temperature function
must be perpendicular to an insulated surface since the slope of temperature at
the surface must be zero.
Another Special Case: Thermal Symmetry
Some heat transfer problems possess thermal symmetry as a result of the
symmetry in imposed thermal conditions. For example, the two surfaces of
a large hot plate of thickness L suspended vertically in air is subjected to
the same thermal conditions, and thus the temperature distribution in one
half of the plate is the same as that in the other half. That is, the heat trans-
fer problem in this plate possesses thermal symmetry about the center plane
at x L/2. Also, the direction of heat flow at any point in the plate is to-
ward the surface closer to the point, and there is no heat flow across the
center plane. Therefore, the center plane can be viewed as an insulated sur-
face, and the thermal condition at this plane of symmetry can be expressed
as (Fig. 2–30)
0 (2–50)
which resembles the insulation or zero heat flux boundary condition. This re-
sult can also be deduced from a plot of temperature distribution with a maxi-
mum, and thus zero slope, at the center plane.
In the case of cylindrical (or spherical) bodies having thermal symmetry
about the center line (or midpoint), the thermal symmetry boundary condition
requires that the first derivative of temperature with respect to r (the radial
variable) be zero at the centerline (or the midpoint).
T(L/2, t)
x
T(0, t)
x
T(0, t)
x
81
CHAPTER 2
T(L, t) = 60°C
= 0
∂T(0, t)
∂x
60°CInsulation T(x, t)
0
L
x
FIGURE 2–29
A plane wall with insulation
and specified temperature
boundary conditions.
= 0
∂T(L/2, t)
————
∂x
Temperature
distribution
(symmetric
about center
plane)
Center plane
Zero
slope
0
L
x
L
—
2
FIGURE 2–30
Thermal symmetry boundary
condition at the center plane
of a plane wall.
cengel_ch02.qxd 1/5/10 10:46 AM Page 81

3 Convection Boundary Condition
Convection is probably the most common boundary condition encountered in
practice since most heat transfer surfaces are exposed to an environment at a
specified temperature. The convection boundary condition is based on a
surface energy balance expressed as
冢
Heat convection
at the surface in
the same direction
冣冢
Heat conduction
at the surface in a
selected direction
冣
82
HEAT CONDUCTION EQUATION
EXAMPLE 2–6
Heat Flux Boundary Condition
Consider an aluminum pan used to cook beef stew on top of an electric range.
The bottom section of the pan is
L
0.3 cm thick and has a diameter of
D
20 cm. The electric heating unit on the range top consumes 800 W of power
during cooking, and 90 percent of the heat generated in the heating element
is transferred to the pan. During steady operation, the temperature of the inner
surface of the pan is measured to be 110°C. Express the boundary conditions
for the bottom section of the pan during this cooking process.
SOLUTION An aluminum pan on an electric range top is considered. The
boundary conditions for the bottom of the pan are to be obtained.
Analysis
The heat transfer through the bottom section of the pan is from the
bottom surface toward the top and can reasonably be approximated as being
one-dimensional. We take the direction normal to the bottom surfaces of the
pan as the
x
axis with the origin at the outer surface, as shown in Fig. 2–31.
Then the inner and outer surfaces of the bottom section of the pan can be rep-
resented by
x
0 and
x
L
, respectively. During steady operation, the tem-
perature will depend on
x
only and thus
T
T
(
x
).
The boundary condition on the outer surface of the bottom of the pan at
x
0 can be approximated as being specified heat flux since it is stated that
90 percent of the 800 W (i.e., 720 W) is transferred to the pan at that surface.
Therefore,
k q
·
0
where
q
·
0
22.9 kW/m
2
The temperature at the inner surface of the bottom of the pan is specified to
be 110°C. Then the boundary condition on this surface can be expressed as
T(L) 110°C
where
L
0.003 m.
Discussion
Note that the determination of the boundary conditions may require
some reasoning and approximations.
0.720 kW
p(0.1 m)
2
Heat transfer rate
Bottom surface area
dT(0)
dx
Water
110°C
x
L
0
q
0
.
FIGURE 2–31
Schematic for Example 2–6.
cengel_ch02.qxd 1/5/10 10:46 AM Page 82

For one-dimensional heat transfer in the x-direction in a plate of thickness L,
the convection boundary conditions on both surfaces can be expressed as
k h
1
[T
1
T(0, t)] (2–51a)
and
k h
2
[T(L, t) T
2
] (2–51b)
where h
1
and h
2
are the convection heat transfer coefficients and T
1
and T
2
are the temperatures of the surrounding mediums on the two sides of the plate,
as shown in Fig. 2–32.
In writing Eqs. 2–51 for convection boundary conditions, we have selected
the direction of heat transfer to be the positive x-direction at both surfaces. But
those expressions are equally applicable when heat transfer is in the opposite
direction at one or both surfaces since reversing the direction of heat transfer
at a surface simply reverses the signs of both conduction and convection terms
at that surface. This is equivalent to multiplying an equation by 1, which has
no effect on the equality (Fig. 2–33). Being able to select either direction as
the direction of heat transfer is certainly a relief since often we do not know
the surface temperature and thus the direction of heat transfer at a surface in
advance. This argument is also valid for other boundary conditions such as the
radiation and combined boundary conditions discussed shortly.
Note that a surface has zero thickness and thus no mass, and it cannot store
any energy. Therefore, the entire net heat entering the surface from one side
must leave the surface from the other side. The convection boundary condition
simply states that heat continues to flow from a body to the surrounding
medium at the same rate, and it just changes vehicles at the surface from con-
duction to convection (or vice versa in the other direction). This is analogous
to people traveling on buses on land and transferring to the ships at the shore.
If the passengers are not allowed to wander around at the shore, then the rate
at which the people are unloaded at the shore from the buses must equal the
rate at which they board the ships. We may call this the conservation of “peo-
ple” principle.
Also note that the surface temperatures T(0, t) and T(L, t) are not known (if
they were known, we would simply use them as the specified temperature
boundary condition and not bother with convection). But a surface tempera-
ture can be determined once the solution T(x, t) is obtained by substituting the
value of x at that surface into the solution.
T(L, t)
x
T(0, t)
x
83
CHAPTER 2
0
Convection Conduction
L
x
ConvectionConduction
h
1
T
⬁
1
h
2
T
⬁
2
∂T(0, t)
∂x
h
1
[T
⬁1
– T(0, t)] = –k
∂T(L, t)
∂x
–k
= h
2
[T(L, t) – T
⬁2
]
FIGURE 2–32
Convection boundary conditions on
the two surfaces of a plane wall.
0
Convection Conduction
L
x
Convection Conduction
h
1
, T
⬁
1
∂T(0, t)
———
∂x
h
1
[T
⬁1
– T(0, t)] = –k
h
1
[T(0, t) – T
⬁1
] = k
∂T(0, t)
———
∂x
FIGURE 2–33
The assumed direction of heat transfer
at a boundary has no effect on the
boundary condition expression.
EXAMPLE 2–7
Convection and Insulation Boundary Conditions
Steam flows through a pipe shown in Fig. 2–34 at an average temperature
of
T
200°C. The inner and outer radii of the pipe are
r
1
8 cm and
r
2
8.5 cm, respectively, and the outer surface of the pipe is heavily insulated. If
the convection heat transfer coefficient on the inner surface of the pipe is
h
65 W/m
2
·K, express the boundary conditions on the inner and outer surfaces of
the pipe during transient periods.
cengel_ch02.qxd 1/5/10 10:46 AM Page 83

4 Radiation Boundary Condition
In some cases, such as those encountered in space and cryogenic applications,
a heat transfer surface is surrounded by an evacuated space and thus there is
no convection heat transfer between a surface and the surrounding medium. In
such cases, radiation becomes the only mechanism of heat transfer between
the surface under consideration and the surroundings. Using an energy bal-
ance, the radiation boundary condition on a surface can be expressed as
For one-dimensional heat transfer in the x-direction in a plate of thickness L,the
radiation boundary conditions on both surfaces can be expressed as (Fig. 2–35)
k e
1
s[T
4
surr, 1
T(0, t)
4
] (2–52a)
and
k e
2
s[T(L, t)
4
T
4
surr, 2
] (2–52b)
where e
1
and e
2
are the emissivities of the boundary surfaces, s 5.67
10
8
W/m
2
·K
4
is the Stefan–Boltzmann constant, and T
surr, 1
and T
surr, 2
are the
average temperatures of the surfaces surrounding the two sides of the plate,
respectively. Note that the temperatures in radiation calculations must be ex-
pressed in K or R (not in °C or °F).
The radiation boundary condition involves the fourth power of temperature,
and thus it is a nonlinear condition. As a result, the application of this boundary
condition results in powers of the unknown coefficients, which makes it difficult
T(L, t)
x
T(0, t)
x
冢
Radiation exchange
at the surface in
the same direction
冣冢
Heat conduction
at the surface in a
selected direction
冣
84
HEAT CONDUCTION EQUATION
SOLUTION The flow of steam through an insulated pipe is considered.
The boundary conditions on the inner and outer surfaces of the pipe are to be
obtained.
Analysis
During initial transient periods, heat transfer through the pipe mate-
rial predominantly is in the radial direction, and thus can be approximated as
being one-dimensional. Then the temperature within the pipe material changes
with the radial distance
r
and the time
t
. That is,
T
T
(
r, t
).
It is stated that heat transfer between the steam and the pipe at the inner
surface is by convection. Then taking the direction of heat transfer to be the
positive
r
direction, the boundary condition on that surface can be expressed as
k h[T
T(r
1
)]
The pipe is said to be well insulated on the outside, and thus heat loss through
the outer surface of the pipe can be assumed to be negligible. Then the bound-
ary condition at the outer surface can be expressed as
0
Discussion
Note that the temperature gradient must be zero on the outer sur-
face of the pipe at all times.
T(r
2
, t)
r
T(r
1
, t)
r
Insulation
r
1
r
2
h
T
⬁
FIGURE 2–34
Schematic for Example 2–7.
0
Radiation Conduction
L
x
RadiationConduction
1
T
surr, 1
ε
2
T
surr, 2
ε
e
1
[T
surr, 1
– T(0, t)
4
] = –k
∂T(0, t)
———
∂x
4
s
=–k
∂T(L, t)
———
∂x
2
[T(L, t)
4
– T
surr, 2
]
ε
4
s
FIGURE 2–35
Radiation boundary conditions on
both surfaces of a plane wall.
cengel_ch02.qxd 1/5/10 10:46 AM Page 84

to determine them. Therefore, it is tempting to ignore radiation exchange at a
surface during a heat transfer analysis in order to avoid the complications asso-
ciated with nonlinearity. This is especially the case when heat transfer at the sur-
face is dominated by convection, and the role of radiation is minor.
5 Interface Boundary Conditions
Some bodies are made up of layers of different materials, and the solution of
a heat transfer problem in such a medium requires the solution of the heat
transfer problem in each layer. This, in turn, requires the specification of the
boundary conditions at each interface.
The boundary conditions at an interface are based on the requirements that
(1) two bodies in contact must have the same temperature at the area of con-
tact and (2) an interface (which is a surface) cannot store any energy, and thus
the heat flux on the two sides of an interface must be the same. The boundary
conditions at the interface of two bodies A and B in perfect contact at x x
0
can be expressed as (Fig. 2–36)
T
A
(x
0
, t) T
B
(x
0
, t) (2–53)
and
k
A
k
B
(2–54)
where k
A
and k
B
are the thermal conductivities of the layers A and B, respec-
tively. The case of imperfect contact results in thermal contact resistance,
which is considered in the next chapter.
6 Generalized Boundary Conditions
So far we have considered surfaces subjected to single mode heat transfer,
such as the specified heat flux, convection, or radiation for simplicity. In gen-
eral, however, a surface may involve convection, radiation, and specified heat
flux simultaneously. The boundary condition in such cases is again obtained
from a surface energy balance, expressed as
(2–55)
This is illustrated in Examples 2–8 and 2–9.
°
Heat transfer
from the surface
in all modes
¢°
Heat transfer
to the surface
in all modes
¢
T
B
(x
0
, t)
x
T
A
(x
0
, t)
x
85
CHAPTER 2
ConductionConduction
Material
A
Material
B
Interface
0
L
x
0
x
T
A
(x
0
, t) = T
B
(x
0
, t)
T
A
(x, t)
T
B
(x, t)
= –
k
B
–k
A
∂T
B
(x
0
, t)
∂x
∂T
A
(x
0
, t)
∂x
FIGURE 2–36
Boundary conditions at the interface
of two bodies in perfect contact.
EXAMPLE 2–8
Combined Convection and Radiation Condition
A spherical metal ball of radius
r
o
is heated in an oven to a temperature of
600°F throughout and is then taken out of the oven and allowed to cool in am-
bient air at
T
78°F, as shown in Fig. 2–37. The thermal conductivity of the
ball material is
k
8.3 Btu/h·ft·R, and the average convection heat transfer
coefficient on the outer surface of the ball is evaluated to be
h
4.5
Btu/h·ft
2
·R. The emissivity of the outer surface of the ball is e 0.6, and the
average temperature of the surrounding surfaces is
T
surr
525 R. Assuming
the ball is cooled uniformly from the entire outer surface, express the initial
and boundary conditions for the cooling process of the ball.
Convection
T
i
= 600°F
Metal
ball
Conduction
Radiation
r
o
r
0
T
surr
= 525 R
T
⬁
= 78°F
FIGURE 2–37
Schematic for Example 2–8.
cengel_ch02.qxd 1/5/10 10:46 AM Page 85

86
HEAT CONDUCTION EQUATION
SOLUTION The cooling of a hot spherical metal ball is considered. The initial
and boundary conditions are to be obtained.
Analysis
The ball is initially at a uniform temperature and is cooled uniformly
from the entire outer surface. Therefore, this is a one-dimensional transient
heat transfer problem since the temperature within the ball changes with the
radial distance
r
and the time
t
. That is,
T
T
(
r, t
). Taking the moment
the ball is removed from the oven to be
t
0, the initial condition can be
expressed as
T(r, 0) T
i
600°F
The problem possesses symmetry about the midpoint (
r
0) since the
isotherms in this case are concentric spheres, and thus no heat is crossing the
midpoint of the ball. Then the boundary condition at the midpoint can be ex-
pressed as
0
The heat conducted to the outer surface of the ball is lost to the environment
by convection and radiation. Then taking the direction of heat transfer to be
the positive
r
direction, the boundary condition on the outer surface can be ex-
pressed as
k h[T(r
o
) T
] es[T(r
o
)
4
T
4
surr
]
Discussion
All the quantities in the above relations are known except the tem-
peratures and their derivatives at
r
0 and
r
o
. Also, the radiation part of the
boundary condition is often ignored for simplicity by modifying the convection
heat transfer coefficient to account for the contribution of radiation. The convec-
tion coefficient
h
in that case becomes the combined heat transfer coefficient.
T(r
o
, t)
r
T(0, t)
r
EXAMPLE 2–9
Combined Convection, Radiation, and Heat Flux
Consider the south wall of a house that is
L
0.2 m thick. The outer surface
of the wall is exposed to solar radiation and has an absorptivity of a 0.5 for
solar energy. The interior of the house is maintained at
T
1
20°C, while the
ambient air temperature outside remains at
T
2
5°C. The sky, the ground,
and the surfaces of the surrounding structures at this location can be modeled
as a surface at an effective temperature of
T
sky
255 K for radiation exchange
on the outer surface. The radiation exchange between the inner surface of
the wall and the surfaces of the walls, floor, and ceiling it faces is negligible.
The convection heat transfer coefficients on the inner and the outer surfaces of
the wall are
h
1
6 W/m
2
·K and
h
2
25 W/m
2
·K, respectively. The thermal
conductivity of the wall material is
k
0.7 W/m·K, and the emissivity of the
outer surface is e
2
0.9. Assuming the heat transfer through the wall to be
steady and one-dimensional, express the boundary conditions on the inner and
the outer surfaces of the wall.
SOLUTION The wall of a house subjected to solar radiation is considered. The
boundary conditions on the inner and outer surfaces of the wall are to be ob-
tained.
cengel_ch02.qxd 1/5/10 10:46 AM Page 86

Note that a heat transfer problem may involve different kinds of boundary
conditions on different surfaces. For example, a plate may be subject to heat
flux on one surface while losing or gaining heat by convection from the other
surface. Also, the two boundary conditions in a direction may be specified at
the same boundary, while no condition is imposed on the other boundary. For
example, specifying the temperature and heat flux at x 0 of a plate of thick-
ness L will result in a unique solution for the one-dimensional steady temper-
ature distribution in the plate, including the value of temperature at the surface
x L. Although not necessary, there is nothing wrong with specifying more
than two boundary conditions in a specified direction, provided that there is
no contradiction. The extra conditions in this case can be used to verify the
results.
2–5 SOLUTION OF STEADY ONE-DIMENSIONAL
HEAT CONDUCTION PROBLEMS
So far we have derived the differential equations for heat conduction in vari-
ous coordinate systems and discussed the possible boundary conditions.
A heat conduction problem can be formulated by specifying the applicable
differential equation and a set of proper boundary conditions.
In this section we will solve a wide range of heat conduction problems in
rectangular, cylindrical, and spherical geometries. We will limit our attention
to problems that result in ordinary differential equations such as the steady
one-dimensional heat conduction problems. We will also assume constant
thermal conductivity, but will consider variable conductivity later in this
■
87
CHAPTER 2
Analysis
We take the direction normal to the wall surfaces as the
x
-axis with
the origin at the inner surface of the wall, as shown in Fig. 2–38. The heat
transfer through the wall is given to be steady and one-dimensional, and thus
the temperature depends on
x
only and not on time. That is,
T
T
(
x
).
The boundary condition on the inner surface of the wall at
x
0 is a typical
convection condition since it does not involve any radiation or specified heat
flux. Taking the direction of heat transfer to be the positive
x
-direction, the
boundary condition on the inner surface can be expressed as
k h
1
[T
1
T(0)]
The boundary condition on the outer surface at
x
0 is quite general as it
involves conduction, convection, radiation, and specified heat flux. Again tak-
ing the direction of heat transfer to be the positive
x
-direction, the boundary
condition on the outer surface can be expressed as
k h
2
[T(L) T
2
] e
2
s[T(L)
4
T
4
sky
] aq
·
solar
where
q
·
solar
is the incident solar heat flux.
Discussion
Assuming the opposite direction for heat transfer would give the
same result multiplied by
1, which is equivalent to the relation here. All the
quantities in these relations are known except the temperatures and their de-
rivatives at the two boundaries.
dT(L)
dx
dT(0)
dx
Conduction
ConductionConvection
Convection
Radiation
Solar
T
sky
South
wall
Inner
surface
0
L
x
h
1
T
⬁1
h
2
T
⬁2
Sun
Outer
surface
FIGURE 2–38
Schematic for Example 2–9.
cengel_ch02.qxd 1/5/10 10:46 AM Page 87

chapter. If you feel rusty on differential equations or haven’t taken differential
equations yet, no need to panic. Simple integration is all you need to solve the
steady one-dimensional heat conduction problems.
The solution procedure for solving heat conduction problems can be sum-
marized as (1) formulate the problem by obtaining the applicable differential
equation in its simplest form and specifying the boundary conditions, (2) ob-
tain the general solution of the differential equation, and (3) apply the
boundary conditions and determine the arbitrary constants in the general so-
lution (Fig. 2–39). This is demonstrated below with examples.
88
HEAT CONDUCTION EQUATION
EXAMPLE 2–10
Heat Conduction in a Plane Wall
Consider a large plane wall of thickness
L
0.2 m, thermal conductivity
k
1.2 W/m·K, and surface area
A
15 m
2
. The two sides of the wall are main-
tained at constant temperatures of
T
1
120°C and
T
2
50°C, respectively, as
shown in Fig. 2–40. Determine (
a
) the variation of temperature within the wall
and the value of temperature at
x
0.1 m and (
b
) the rate of heat conduction
through the wall under steady conditions.
SOLUTION A plane wall with specified surface temperatures is given. The
variation of temperature and the rate of heat transfer are to be determined.
Assumptions
1 Heat conduction is steady. 2 Heat conduction is one-
dimensional since the wall is large relative to its thickness and the thermal
conditions on both sides are uniform. 3 Thermal conductivity is constant.
4 There is no heat generation.
Properties
The thermal conductivity is given to be
k
1.2 W/m·K.
Analysis
(
a
) Taking the direction normal to the surface of the wall to be the
x
-direction, the differential equation for this problem can be expressed as
0
with boundary conditions
T(0) T
1
120°C
T(L) T
2
50°C
The differential equation is linear and second order, and a quick inspection of
it reveals that it has a single term involving derivatives and no terms involving
the unknown function
T
as a factor. Thus, it can be solved by direct integration.
Noting that an integration reduces the order of a derivative by one, the general
solution of the differential equation above can be obtained by two simple suc-
cessive integrations, each of which introduces an integration constant.
Integrating the differential equation once with respect to
x
yields
C
1
where
C
1
is an arbitrary constant. Notice that the order of the derivative went
down by one as a result of integration. As a check, if we take the derivative of
this equation, we will obtain the original differential equation. This equation is
not the solution yet since it involves a derivative.
dT
dx
d
2
T
dx
2
Heat transfer problem
Mathematical formulation
(Differential equation and
boundary conditions)
General solution of differential equation
Application of boundary conditions
Solution of the problem
FIGURE 2–39
Basic steps involved in the solution
of heat transfer problems.
T
2
T
1
Plane
wall
0
L
x
FIGURE 2–40
Schematic for Example 2–10.
cengel_ch02.qxd 1/5/10 10:46 AM Page 88

89
CHAPTER 2
Integrating one more time, we obtain
T(x) C
1
x C
2
which is the general solution of the differential equation (Fig. 2–41). The gen-
eral solution in this case resembles the general formula of a straight line whose
slope is
C
1
and whose value at
x
0 is
C
2
. This is not surprising since the sec-
ond derivative represents the change in the slope of a function, and a zero sec-
ond derivative indicates that the slope of the function remains constant.
Therefore,
any straight line
is a solution of this differential equation.
The general solution contains two unknown constants
C
1
and
C
2
, and thus
we need two equations to determine them uniquely and obtain the specific so-
lution. These equations are obtained by forcing the general solution to satisfy
the specified boundary conditions. The application of each condition yields one
equation, and thus we need to specify two conditions to determine the con-
stants
C
1
and
C
2
.
When applying a boundary condition to an equation,
all occurrences of the
dependent and independent variables and any derivatives are replaced by the
specified values.
Thus the only unknowns in the resulting equations are the ar-
bitrary constants.
The first boundary condition can be interpreted as
in the general solution, re-
place all the x’s by zero and T
(
x
)
by T
1
. That is (Fig. 2–42),
T(0) C
1
0 C
2
→ C
2
T
1
The second boundary condition can be interpreted as
in the general solution,
replace all the x’s by L and T
(
x
)
by T
2
. That is,
T(L) C
1
L C
2
→ T
2
C
1
L T
1
→ C
1
Substituting the
C
1
and
C
2
expressions into the general solution, we obtain
T(x) x T
1
(2–56)
which is the desired solution since it satisfies not only the differential equation
but also the two specified boundary conditions. That is, differentiating
Eq. 2–56 with respect to
x
twice will give
d
2
T
/
dx
2
, which is the given differential
equation, and substituting
x
0 and
x
L
into Eq. 2–56 gives
T
(0)
T
1
and
T
(
L
)
T
2
, respectively, which are the specified conditions at the boundaries.
Substituting the given information, the value of the temperature at
x
0.1 m is determined to be
T(0.1 m) (0.1 m) 120°C 85°C
(
b
) The rate of heat conduction anywhere in the wall is determined from
Fourier’s law to be
Q
·
wall
kA kAC
1
kA kA (2–57)
The numerical value of the rate of heat conduction through the wall is deter-
mined by substituting the given values to be
Q
·
kA (1.2 W/m·K)(15 m
2
) 6300 W
Discussion
Note that under steady conditions, the rate of heat conduction
through a plane wall is constant.
(120 50)°C
0.2 m
T
1
T
2
L
T
1
T
2
L
T
2
T
1
L
dT
dx
(50 120)°C
0.2 m
T
2
T
1
L
T
2
T
1
L
d
2
T
dx
2
Differential equation:
= 0
dT
dx
Integrate:
= C
1
General
solution
Arbitrary
constants
T(x) = C
1
x + C
2
Integrate again:
FIGURE 2–41
Obtaining the general solution of a
simple second order differential
equation by integration.
T(0) = T
1
T
1
0
T(x) = C
1
x + C
2
Boundary condition:
General solution:
T
1
= C
1
× 0 + C
2
→ C
2
= T
1
Substituting:
T(x) = C
1
x + C
2
Applying the boundary condition:
0
It cannot involve x or T(x) after the
boundary condition is applied.
}
↑↑
FIGURE 2–42
When applying a boundary condition
to the general solution at a specified
point, all occurrences of the dependent
and independent variables should
be replaced by their specified
values at that point.
cengel_ch02.qxd 1/5/10 10:46 AM Page 89

90
HEAT CONDUCTION EQUATION
EXAMPLE 2–11
A Wall with Various Sets of Boundary
Conditions
Consider steady one-dimensional heat conduction in a large plane wall of
thickness
L
and constant thermal conductivity
k
with no heat generation. Ob-
tain expressions for the variation of temperature within the wall for the follow-
ing pairs of boundary conditions (Fig. 2–43):
(a) k q
·
0
40 W/cm
2
and T(0) T
0
15°C
(b) k q
·
0
40 W/cm
2
and k q
·
L
25 W/cm
2
(c) k q
·
0
40 W/cm
2
and k q
·
L
q
·
0
40 W/cm
2
SOLUTION Steady one-dimensional heat conduction in a large plane wall is
considered. The variation of temperature is to be determined for different sets
of boundary conditions.
Analysis
This is a steady one-dimensional heat conduction problem with con-
stant thermal conductivity and no heat generation in the medium, and the heat
conduction equation in this case can be expressed as (Eq. 2–17)
0
whose general solution was determined in the previous example by direct inte-
gration to be
T(x) C
1
x C
2
where
C
1
and
C
2
are two arbitrary integration constants. The specific solutions
corresponding to each specified pair of boundary conditions are determined as
follows.
(
a
) In this case, both boundary conditions are specified at the same boundary at
x
0, and no boundary condition is specified at the other boundary at
x
L
.
Noting that
C
1
the application of the boundary conditions gives
k q
·
0
→ kC
1
q
·
0
→ C
1
and
T(0) T
0
→ T
0
C
1
0 C
2
→ C
2
T
0
Substituting, the specific solution in this case is determined to be
T(x) x T
0
q
.
0
k
q
.
0
k
dT(0)
dx
dT
dx
d
2
T
dx
2
dT(L)
dx
dT(0)
dx
dT(L)
dx
dT(0)
dx
dT(0)
dx
cengel_ch02.qxd 1/5/10 10:46 AM Page 90

91
CHAPTER 2
Therefore, the two boundary conditions can be specified at the same boundary,
and it is not necessary to specify them at different locations. In fact, the fun-
damental theorem of linear ordinary differential equations guarantees that a
unique solution exists when both conditions are specified at the same location.
But no such guarantee exists when the two conditions are specified at differ-
ent boundaries, as you will see below.
(
b
) In this case different heat fluxes are specified at the two boundaries. The
application of the boundary conditions gives
k q
·
0
→ kC
1
q
·
0
→ C
1
and
k q
·
L
→ kC
1
q
·
L
→ C
1
Since q
·
0
q
·
L
and the constant
C
1
cannot be equal to two different things at
the same time, there is no solution in this case. This is not surprising since this
case corresponds to supplying heat to the plane wall from both sides and ex-
pecting the temperature of the wall to remain steady (not to change with time).
This is impossible.
(
c
) In this case, the same values for heat flux are specified at the two bound-
aries. The application of the boundary conditions gives
k q
·
0
→ kC
1
q
·
0
→ C
1
and
k q
·
0
→ kC
1
q
·
0
→ C
1
Thus, both conditions result in the same value for the constant
C
1
, but no value
for
C
2
. Substituting, the specific solution in this case is determined to be
T(x) x C
2
which is not a unique solution since
C
2
is arbitrary.
q
.
0
k
q
.
0
k
dT(L)
dx
q
.
0
k
dT(0)
dx
q
.
L
k
dT(L)
dx
q
.
0
k
dT(0)
dx
(a)(b)(c)
15°C
Plane
wall
T(x)
40 W/cm
2
0
L
x
Plane
wall
T(x)
40 W/cm
2
25 W/cm
2
0
L
x
Plane
wall
T(x)
40 W/cm
2
40 W/cm
2
0
L
x
FIGURE 2–43
Schematic for Example 2–11.
cengel_ch02.qxd 1/5/10 10:46 AM Page 91

92
HEAT CONDUCTION EQUATION
Discussion
The last solution represents a family of straight lines whose slope
is
q
·
0
/
k.
Physically, this problem corresponds to requiring the rate of heat
supplied to the wall at
x
0 be equal to the rate of heat removal from the
other side of the wall at
x
L
. But this is a consequence of the heat conduc-
tion through the wall being steady, and thus the second boundary condition
does not provide any new information. So it is not surprising that the solution
of this problem is not unique. The three cases discussed above are summarized
in Fig. 2–44.
T˝(x) = 0
T(x) = C
1
x + C
2
x + T
0
T(x) = –
–kT ′(0) = q
0
q
0
k
T ′(0) = T
0
Differential equation:
General solution:
(a) Unique solution:
·
·
x + C
2
T(x) = –
q
0
k
·
T(x) = None
Arbitrary
–kT ′(0) = q
0
–kT ′(L) = q
L
(b) No solution:
·
·
·
–kT ′(0) = q
0
–kT ′(L) = q
0
(c) Multiple solutions:
·
↑
FIGURE 2–44
A boundary-value problem may have
a unique solution, infinitely many
solutions, or no solutions at all.
EXAMPLE 2–12
Heat Conduction in the Base Plate of an Iron
Consider the base plate of a 1200-W household iron that has a thickness of
L
0.5 cm, base area of
A
300 cm
2
, and thermal conductivity of
k
15 W/m·K. The inner surface of the base plate is subjected to uniform heat flux
generated by the resistance heaters inside, and the outer surface loses heat to
the surroundings at
T
20°C by convection, as shown in Fig. 2–45. Taking the
convection heat transfer coefficient to be
h
80 W/m
2
·K and disregarding heat
loss by radiation, obtain an expression for the variation of temperature in the
base plate, and evaluate the temperatures at the inner and the outer surfaces.
SOLUTION The base plate of an iron is considered. The variation of tempera-
ture in the plate and the surface temperatures are to be determined.
Assumptions
1 Heat transfer is steady since there is no change with time.
2 Heat transfer is one-dimensional since the surface area of the base plate is
large relative to its thickness, and the thermal conditions on both sides are uni-
form. 3 Thermal conductivity is constant. 4 There is no heat generation in the
medium. 5 Heat transfer by radiation is negligible. 6 The upper part of the iron
is well insulated so that the entire heat generated in the resistance wires is
transferred to the base plate through its inner surface.
Properties
The thermal conductivity is given to be
k
15 W/m·K.
Analysis
The inner surface of the base plate is subjected to uniform heat flux
at a rate
of
q
·
0
40,000 W/m
2
The outer side of the plate is subjected to the convection condition. Taking the
direction normal to the surface of the wall as the
x
-direction with its origin on
the inner surface, the differential equation for this problem can be expressed
as (Fig. 2–46)
0
with the boundary conditions
k q
·
0
40,000 W/m
2
k h[T(L) T
]
dT(L)
dx
dT(0)
dx
d
2
T
dx
2
1200 W
0.03 m
2
Q
.
0
A
base
x
h
L
Base plate
T
⬁
= 20°C
300 cm
2
Insulation
Resistance heater
1200 W
FIGURE 2–45
Schematic for Example 2–12.
cengel_ch02.qxd 1/5/10 10:46 AM Page 92

93
CHAPTER 2
The general solution of the differential equation is again obtained by two suc-
cessive integrations to be
C
1
and
T(x) C
1
x C
2
(
a
)
where
C
1
and
C
2
are arbitrary constants. Applying the first boundary condition,
k q
·
0
→ kC
1
q
·
0
→ C
1
Noting that
dT
/
dx
C
1
and
T
(
L
)
C
1
L
C
2
, the application of the second
boundary condition gives
k h[T(L) T
] → kC
1
h[(C
1
L C
2
) T
]
Substituting
C
1
q
·
0
/
k
and solving for
C
2
, we obtain
C
2
T
L
Now substituting
C
1
and
C
2
into the general solution (
a
) gives
T(x) T
q
·
0
(
b
)
which is the solution for the variation of the temperature in the plate. The tem-
peratures at the inner and outer surfaces of the plate are determined by sub-
stituting
x
0 and
x
L
, respectively, into the relation (
b
):
T(0) T
q
·
0
20°C (40,000 W/m
2
) 533°C
and
T(L) T
q
·
0
0 20°C 520°C
Discussion
Note that the temperature of the inner surface of the base plate is
13°C higher than the temperature of the outer surface when steady operating
conditions are reached. Also note that this heat transfer analysis enables us to
calculate the temperatures of surfaces that we cannot even reach. This exam-
ple demonstrates how the heat flux and convection boundary conditions are ap-
plied to heat transfer problems.
40,000 W/m
2
80 W/m
2
K
1
h
冣冢
1
80 W/m
2
K
ba
0.005 m
15 W/mK
1
h
冣冢
L
k
1
h
ba
L x
k
q
.
0
k
q
.
0
h
dT(L)
dx
q
.
0
k
dT(0)
dx
dT
dx
0
Heat flux Conduction
Base plate
L
x
Convection
h
T
⬁
Conduction
q
0
= –k
dT(0)
–——
dx
·
–k = h[T(L) – T
⬁
]
dT(L)
–——
dx
FIGURE 2–46
The boundary conditions on the
base plate of the iron discussed
in Example 2–12.
cengel_ch02.qxd 1/5/10 10:46 AM Page 93

94
HEAT CONDUCTION EQUATION
EXAMPLE 2–13
Heat Conduction in a Solar Heated Wall
Consider a large plane wall of thickness
L
0.06 m and thermal conductivity
k
1.2 W/m·K in space. The wall is covered with white porcelain tiles that
have an emissivity of e 0.85 and a solar absorptivity of a 0.26, as shown
in Fig. 2–47. The inner surface of the wall is maintained at
T
1
300 K at all
times, while the outer surface is exposed to solar radiation that is incident at a
rate of
q
·
solar
800 W/m
2
. The outer surface is also losing heat by radiation to
deep space at 0 K. Determine the temperature of the outer surface of the wall
and the rate of heat transfer through the wall when steady operating conditions
are reached. What would your response be if no solar radiation was incident on
the surface?
SOLUTION A plane wall in space is subjected to specified temperature on one
side and solar radiation on the other side. The outer surface temperature and
the rate of heat transfer are to be determined.
Assumptions
1 Heat transfer is steady since there is no change with time.
2 Heat transfer is one-dimensional since the wall is large relative to its
thickness, and the thermal conditions on both sides are uniform. 3 Thermal
conductivity is constant. 4 There is no heat generation.
Properties
The thermal conductivity is given to be
k
1.2 W/m·K.
Analysis
Taking the direction normal to the surface of the wall as the
x
-direction with its origin on the inner surface, the differential equation for this
problem can be expressed as
0
with boundary conditions
T(0) T
1
300 K
k es[T(L)
4
T
4
space
] q
·
solar
where
T
space
0. The general solution of the differential equation is again
obtained by two successive integrations to be
T(x) C
1
x C
2
(
a
)
where
C
1
and
C
2
are arbitrary constants. Applying the first boundary condition
yields
T(0) C
1
0 C
2
→ C
2
T
1
Noting that
dT
/
dx
C
1
and
T
(
L
)
C
1
L
C
2
C
1
L
T
1
, the application of
the second boundary conditions gives
k esT(L)
4
aq
·
solar
→ kC
1
es(C
1
L T
1
)
4
aq
·
solar
Although
C
1
is the only unknown in this equation, we cannot get an explicit ex-
pression for it because the equation is nonlinear, and thus we cannot get a
closed-form expression for the temperature distribution. This should explain
why we do our best to avoid nonlinearities in the analysis, such as those asso-
ciated with radiation.
dT(L)
dx
dT(L)
dx
d
2
T
dx
2
0
Plane wall
L
x
ε
α
Conduction
Space
Radiation
Solar
Sun
T
1
FIGURE 2–47
Schematic for Example 2–13.
cengel_ch02.qxd 1/5/10 10:46 AM Page 94

95
CHAPTER 2
Let us back up a little and denote the outer surface temperature by
T
(
L
)
T
L
instead of
T
(
L
)
C
1
L
T
1
. The application of the second boundary condition
in this case gives
k esT(L)
4
aq
·
solar
→ kC
1
es q
·
solar
Solving for
C
1
gives
C
1
(
b
)
Now substituting
C
1
and
C
2
into the general solution (
a
), we obtain
T(x) x T
1
(
c
)
which is the solution for the variation of the temperature in the wall in terms of
the unknown outer surface temperature
T
L
. At
x
L
it becomes
T
L
L T
1
(
d
)
which is an implicit relation for the outer surface temperature
T
L
. Substituting
the given values, we get
T
L
(0.06 m) 300 K
which simplifies to
T
L
310.4 0.240975
This equation can be solved by one of the several nonlinear equation solvers
available (or by the old fashioned trial-and-error method) to give (Fig. 2–48)
T
L
292.7 K
Knowing the outer surface temperature and knowing that it must remain
constant under steady conditions, the temperature distribution in the wall can
be determined by substituting the
T
L
value above into Eq. (
c
):
T(x) x 300 K
which simplifies to
T(x) (121.5 K/m)x 300 K
Note that the outer surface temperature turned out to be lower than the inner
surface temperature. Therefore, the heat transfer through the wall is toward the
outside despite the absorption of solar radiation by the outer surface. Knowing
both the inner and outer surface temperatures of the wall, the steady rate of
heat conduction through the wall can be determined from
q
·
k (1.2 W/m·K) 146 W/m
2
(300 292.7) K
0.06 m
T
1
T
L
L
0.26 (800 W/m
2
) 0.85 (5.67 10
8
W/m
2
.
K
4
)(292.7 K)
4
1.2 W/m
.
K
冢
T
L
100
冣
4
0.26 (800 W/m
2
) 0.85 (5.67 10
8
W/m
2
K
4
) T
4
L
1.2 W/mK
aq
.
solar
esT
4
L
k
aq
.
solar
esT
4
L
k
aq
.
solar
esT
4
L
k
T
4
L
dT(L)
dx
T
L
= 310.4 – 0.240975
T
L
= 290.2 K
T
L
= 293.1 K
T
L
100
(1) Rearrange the equation to be solved:
(2) Guess the value of T
L
, say 300 K, and
substitute into the right side of the equation.
It gives
(3) Now substitute this value of T
L
into the
right side of the equation and get
T
L
= 292.6 K
T
L
= 292.7 K
T
L
= 292.7 K
(4) Repeat step (3) until convergence to
desired accuracy is achieved. The
subsequent iterations give
Therefore, the solution is T
L
= 292.7 K. The
result is independent of the initial guess.
The equation is in the proper form since the
left side consists of T
L
only.
4
FIGURE 2–48
A simple method of solving a
nonlinear equation is to arrange the
equation such that the unknown is
alone on the left side while everything
else is on the right side, and to iterate
after an initial guess until
convergence.
cengel_ch02.qxd 1/5/10 10:46 AM Page 95

96
HEAT CONDUCTION EQUATION
Discussion
In the case of no incident solar radiation, the outer surface tem-
perature, determined from Eq. (
d
) by setting q
·
solar
0, is
T
L
284.3 K. It is
interesting to note that the solar energy incident on the surface causes the sur-
face temperature to increase by about 8 K only when the inner surface tem-
perature of the wall is maintained at 300 K.
EXAMPLE 2–14
Heat Loss through a Steam Pipe
Consider a steam pipe of length
L
20 m, inner radius
r
1
6 cm, outer radius
r
2
8 cm, and thermal conductivity
k
20 W/m·K, as shown in Fig. 2–49.
The inner and outer surfaces of the pipe are maintained at average tempera-
tures of
T
1
150°C and
T
2
60°C, respectively. Obtain a general relation for
the temperature distribution inside the pipe under steady conditions, and de-
termine the rate of heat loss from the steam through the pipe.
SOLUTION A steam pipe is subjected to specified temperatures on its sur-
faces. The variation of temperature and the rate of heat transfer are to be de-
termined.
Assumptions
1 Heat transfer is steady since there is no change with time.
2 Heat transfer is one-dimensional since there is thermal symmetry about the
centerline and no variation in the axial direction, and thus
T
T
(
r
). 3 Thermal
conductivity is constant. 4 There is no heat generation.
Properties
The thermal conductivity is given to be
k
20 W/m·K.
Analysis
The mathematical formulation of this problem can be expressed as
0
with boundary conditions
T(r
1
) T
1
150°C
T(r
2
) T
2
60°C
Integrating the differential equation once with respect to
r
gives
r C
1
where
C
1
is an arbitrary constant. We now divide both sides of this equation by
r
to bring it to a readily integrable form,
Again integrating with respect to
r
gives (Fig. 2–50)
T(r) C
1
ln r C
2
(
a
)
We now apply both boundary conditions by replacing all occurrences of
r
and
T
(
r
) in Eq. (
a
) with the specified values at the boundaries. We get
T(r
1
) T
1
→ C
1
ln r
1
C
2
T
1
T(r
2
) T
2
→ C
1
ln r
2
C
2
T
2
C
1
r
dT
dr
dT
dr
冢
r
dT
dr
冣
d
dr
L
0
T
2
T
1
r
1
r
2
r
FIGURE 2–49
Schematic for Example 2–14.
dT
dr
r = 0
Differential equation:
d
dr
dT
dr
r = C
1
Integrate:
T(r) = C
1
In r + C
2
Integrate again:
which is the general solution.
dT
dr
=
Divide by r (r ≠ 0):
C
1
r
FIGURE 2–50
Basic steps involved in the solution
of the steady one-dimensional
heat conduction equation in
cylindrical coordinates.
cengel_ch02.qxd 1/5/10 10:46 AM Page 96

97
CHAPTER 2
which are two equations in two unknowns,
C
1
and
C
2
. Solving them simultane-
ously gives
C
1
and C
2
T
1
ln r
1
Substituting them into Eq. (
a
) and rearranging, the variation of temperature
within the pipe is determined to be
T(r) (T
2
T
1
) T
1
(2–58)
The rate of heat loss from the steam is simply the total rate of heat conduction
through the pipe, and is determined from Fourier’s law to be
Q
·
cylinder
kA k(2prL) 2pkLC
1
2pkL (2–59)
The numerical value of the rate of heat conduction through the pipe is deter-
mined by substituting the given values
Q
·
2p(20 W/m·K)(20 m) 786 kW
Discussion
Note that the total rate of heat transfer through a pipe is constant,
but the heat flux
q
·
Q
·
/(2p
rL
) is not since it decreases in the direction of heat
transfer with increasing radius.
(150 60)°C
ln(0.08/0.06)
T
1
T
2
ln(r
2
/r
1
)
C
1
r
dT
dr
ln(r/r
1
)
ln(r
2
/r
1
)
T
2
T
1
ln(r
2
/r
1
)
T
2
T
1
ln(r
2
/r
1
)
EXAMPLE 2–15
Heat Conduction through a Spherical Shell
Consider a spherical container of inner radius
r
1
8 cm, outer radius
r
2
10 cm, and thermal conductivity
k
45 W/m·K, as shown in Fig. 2–51. The
inner and outer surfaces of the container are maintained at constant tempera-
tures of
T
1
200°C and
T
2
80°C, respectively, as a result of some chemical
reactions occurring inside. Obtain a general relation for the temperature distri-
bution inside the shell under steady conditions, and determine the rate of heat
loss from the container.
SOLUTION A spherical container is subjected to specified temperatures on its
surfaces. The variation of temperature and the rate of heat transfer are to be
determined.
Assumptions
1 Heat transfer is steady since there is no change with time.
2 Heat transfer is one-dimensional since there is thermal symmetry about the
midpoint, and thus
T
T
(
r
). 3 Thermal conductivity is constant. 4 There is no
heat generation.
Properties
The thermal conductivity is given to be
k
45 W/m·K.
Analysis
The mathematical formulation of this problem can be expressed as
0
冢
r
2
dT
dr
冣
d
dr
0
r
1
T
1
T
2
r
2
r
FIGURE 2–51
Schematic for Example 2–15.
cengel_ch02.qxd 1/5/10 10:47 AM Page 97

98
HEAT CONDUCTION EQUATION
with boundary conditions
T(r
1
) T
1
200°C
T(r
2
) T
2
80°C
Integrating the differential equation once with respect to
r
yields
r
2
C
1
where
C
1
is an arbitrary constant. We now divide both sides of this equation by
r
2
to bring it to a readily integrable form,
Again integrating with respect to
r
gives
T(r) C
2
(
a
)
We now apply both boundary conditions by replacing all occurrences of
r
and
T
(
r
) in the relation above by the specified values at the boundaries. We get
T(r
1
) T
1
→ C
2
T
1
T(r
2
) T
2
→ C
2
T
2
which are two equations in two unknowns,
C
1
and
C
2
. Solving them simultane-
ously gives
C
1
(T
1
T
2
) and C
2
Substituting into Eq. (
a
), the variation of temperature within the spherical shell
is determined to be
T(r) (T
1
T
2
) (2–60)
The rate of heat loss from the container is simply the total rate of heat con-
duction through the container wall and is determined from Fourier’s law
Q
·
sphere
kA k(4pr
2
) 4pkC
1
4pkr
1
r
2
(2–61)
The numerical value of the rate of heat conduction through the wall is deter-
mined by substituting the given values to be
Q
·
4p(45 W/m·K)(0.08 m)(0.10 m) 27.1 kW
Discussion
Note that the total rate of heat transfer through a spherical shell is
constant, but the heat flux
q
·
Q
·
/4p
r
2
is not since it decreases in the direc-
tion of heat transfer with increasing radius as shown in Fig. 2–52.
(200 80)°C
(0.10 0.08) m
T
1
T
2
r
2
r
1
C
1
r
2
dT
dr
r
2
T
2
r
1
T
1
r
2
r
1
r
1
r
2
r (r
2
r
1
)
r
2
T
2
r
1
T
1
r
2
r
1
r
1
r
2
r
2
r
1
C
1
r
2
C
1
r
1
C
1
r
C
1
r
2
dT
dr
dT
dr
Q
2
= Q
1
··
q
2
< q
1
··
0
r
1
r
2
r
Q
1
·
q
1
·
= = 337 kW/m
2
q
1
=
·
27.1 kW
—————
4 (0.08 m)
2
Q
1
—
A
1
π
·
= = 216 kW/m
2
q
2
=
·
27.1 kW
—————
4 (0.10 m)
2
Q
2
—
A
2
π
·
FIGURE 2–52
During steady one-dimensional
heat conduction in a spherical (or
cylindrical) container, the total rate
of heat transfer remains constant,
but the heat flux decreases with
increasing radius.
cengel_ch02.qxd 1/5/10 10:47 AM Page 98

2–6 HEAT GENERATION IN A SOLID
Many practical heat transfer applications involve the conversion of some form
of energy into thermal energy in the medium. Such mediums are said to in-
volve internal heat generation, which manifests itself as a rise in temperature
throughout the medium. Some examples of heat generation are resistance
heating in wires, exothermic chemical reactions in a solid, and nuclear reac-
tions in nuclear fuel rods where electrical, chemical, and nuclear energies are
converted to heat, respectively (Fig. 2–53). The absorption of radiation
throughout the volume of a semitransparent medium such as water can also be
considered as heat generation within the medium, as explained earlier.
Heat generation is usually expressed per unit volume of the medium, and is
denoted by e
·
gen
, whose unit is W/m
3
. For example, heat generation in an elec-
trical wire of outer radius r
o
and length L can be expressed as
e
·
gen
(W/m
3
) (2–62)
where I is the electric current and R
e
is the electrical resistance of the wire.
The temperature of a medium rises during heat generation as a result of the
absorption of the generated heat by the medium during transient start-up
period. As the temperature of the medium increases, so does the heat transfer
from the medium to its surroundings. This continues until steady operating
conditions are reached and the rate of heat generation equals the rate of heat
transfer to the surroundings. Once steady operation has been established, the
temperature of the medium at any point no longer changes.
The maximum temperature T
max
in a solid that involves uniform heat genera-
tion occurs at a location farthest away from the outer surface when the outer
surface of the solid is maintained at a constant temperature T
s
. For example, the
maximum temperature occurs at the midplane in a plane wall, at the centerline
in a long cylinder, and at the midpoint in a sphere. The temperature distribution
within the solid in these cases is symmetrical about the center of symmetry.
The quantities of major interest in a medium with heat generation are the
surface temperature T
s
and the maximum temperature T
max
that occurs in the
medium in steady operation. Below we develop expressions for these two
quantities for common geometries for the case of uniform heat generation
(e
·
gen
constant) within the medium.
Consider a solid medium of surface area A
s
, volume
V
, and constant thermal
conductivity k, where heat is generated at a constant rate of e
·
gen
per unit vol-
ume. Heat is transferred from the solid to the surrounding medium at T
, with
a constant heat transfer coefficient of h. All the surfaces of the solid are main-
tained at a common temperature T
s
. Under steady conditions, the energy bal-
ance for this solid can be expressed as (Fig. 2–54)
(2–63)
or
Q
·
e
·
gen
V
(W) (2–64)
冢
Rate of
energy generation
within the solid
冣冢
Rate of
heat transfer
from the solid
冣
I
2
R
e
pr
2
o
L
E
.
gen, electric
V
wire
■
99
CHAPTER 2
Electric
resistance
wires
Nuclear
fuel rods
Chemical
reactions
FIGURE 2–53
Heat generation in solids is
commonly encountered in practice.
Q = E
gen
··
Heat generation
h, T
⬁
T
s
V
k
E
gen
= e
gen
V
·
·
FIGURE 2–54
At steady conditions, the entire heat
generated in a solid must leave the
solid through its outer surface.
cengel_ch02.qxd 1/5/10 10:47 AM Page 99

Disregarding radiation (or incorporating it in the heat transfer coefficient h),
the heat transfer rate can also be expressed from Newton’s law of cooling as
Q
·
hA
s
(T
s
T
) (W) (2–65)
Combining Eqs. 2–64 and 2–65 and solving for the surface temperature T
s
gives
T
s
T
(2–66)
For a large plane wall of thickness 2L (A
s
2A
wall
and
V
2LA
wall
) with both
sides of the wall maintained at the same temperature T
s
, a long solid cylinder
of radius r
o
(A
s
2pr
o
L and
V
pr
2
o
L), and a solid sphere of radius r
o
(A
s
4pr
2
o
and
V
pr
3
o
), Eq. 2–66 reduces to
T
s, plane wall
T
(2–67)
T
s, cylinder
T
(2–68)
T
s, sphere
T
(2–69)
Note that the rise in surface temperature T
s
is due to heat generation in the
solid.
Reconsider heat transfer from a long solid cylinder with heat generation.
We mentioned above that, under steady conditions, the entire heat generated
within the medium is conducted through the outer surface of the cylinder.
Now consider an imaginary inner cylinder of radius r within the cylinder
(Fig. 2–55). Again the heat generated within this inner cylinder must be equal
to the heat conducted through its outer surface. That is, from Fourier’s law of
heat conduction,
kA
r
e
·
gen
V
r
(2–70)
where A
r
2prL and
V
r
pr
2
L at any location r. Substituting these expres-
sions into Eq. 2–70 and separating the variables, we get
k(2prL) e
·
gen
(pr
2
L) → dT rdr
Integrating from r 0 where T(0) T
0
to r r
o
where T(r
o
) T
s
yields
T
max, cylinder
T
0
T
s
(2–71)
where T
0
is the centerline temperature of the cylinder, which is the maximum
temperature, and T
max
is the difference between the centerline and the sur-
face temperatures of the cylinder, which is the maximum temperature rise in
the cylinder above the surface temperature. Once T
max
is available, the cen-
terline temperature can easily be determined from (Fig. 2–56)
T
center
T
0
T
s
T
max
(2–72)
e
.
gen
r
2
o
4k
e
.
gen
2k
dT
dr
dT
dr
e
.
gen
r
o
3h
e
.
gen
r
o
2h
e
.
gen
L
h
4
3
e
.
gen
V
hA
s
100
HEAT CONDUCTION EQUATION
Q = E
gen
··
A
r
V
r
r
o
r
E
gen
= e
gen
V
r
·
·
FIGURE 2–55
Heat conducted through a cylindrical
shell of radius r is equal to the heat
generated within a shell.
Heat generation
Symmetry
line
T
⬁
T
⬁
T
s
T
s
T
0
= T
max
ΔT
max
FIGURE 2–56
The maximum temperature in
a symmetrical solid with uniform
heat generation occurs at its center.
cengel_ch02.qxd 1/5/10 10:47 AM Page 100

The approach outlined above can also be used to determine the maximum tem-
perature rise in a plane wall of thickness 2L with both sides of the wall main-
tained at the same temperature T
s
and a solid sphere of radius r
o
, with these
results:
T
max, plane wall
(2–73)
T
max, sphere
(2–74)
Again the maximum temperature at the center can be determined from
Eq. 2–72 by adding the maximum temperature rise to the surface temperature
of the solid.
e
.
gen
r
2
o
6k
e
.
gen
L
2
2k
101
CHAPTER 2
EXAMPLE 2–16
Centerline Temperature of a Resistance Heater
A 2-kW resistance heater wire whose thermal conductivity is
k
15 W/m·K has
a diameter of
D
4 mm and a length of
L
0.5 m, and is used to boil water
(Fig. 2–57). If the outer surface temperature of the resistance wire is
T
s
105°C, determine the temperature at the center of the wire.
SOLUTION The center temperature of a resistance heater submerged in water
is to be determined.
Assumptions
1 Heat transfer is steady since there is no change with time. 2
Heat transfer is one-dimensional since there is thermal symmetry about the
centerline and no change in the axial direction. 3 Thermal conductivity is con-
stant. 4 Heat generation in the heater is uniform.
Properties
The thermal conductivity is given to be
k
15 W/m·K.
Analysis
The 2-kW resistance heater converts electric energy into heat at a
rate of 2 kW. The heat generation per unit volume of the wire is
e
·
gen
0.318 10
9
W/m
3
Then the center temperature of the wire is determined from Eq. 2–71 to be
T
0
T
s
105°C 126°C
Discussion
Note that the temperature difference between the center and the
surface of the wire is 21°C. Also, the thermal conductivity units W/m·°C and
W/m·K are equivalent.
(0.318 10
9
W/m
3
)(0.002 m)
2
4 (15 W/m
.
C)
e
.
gen
r
2
o
4k
2000 W
p(0.002 m)
2
(0.5 m)
E
.
gen
pr
2
o
L
E
.
gen
V
wire
We have developed these relations using the intuitive energy balance
approach. However, we could have obtained the same relations by setting
up the appropriate differential equations and solving them, as illustrated in
Examples 2–17 and 2–18.
D = 4 mm
Water
T
s
= 105°C
T
0
e
gen
·
Q
·
FIGURE 2–57
Schematic for Example 2–16.
cengel_ch02.qxd 1/5/10 10:47 AM Page 101
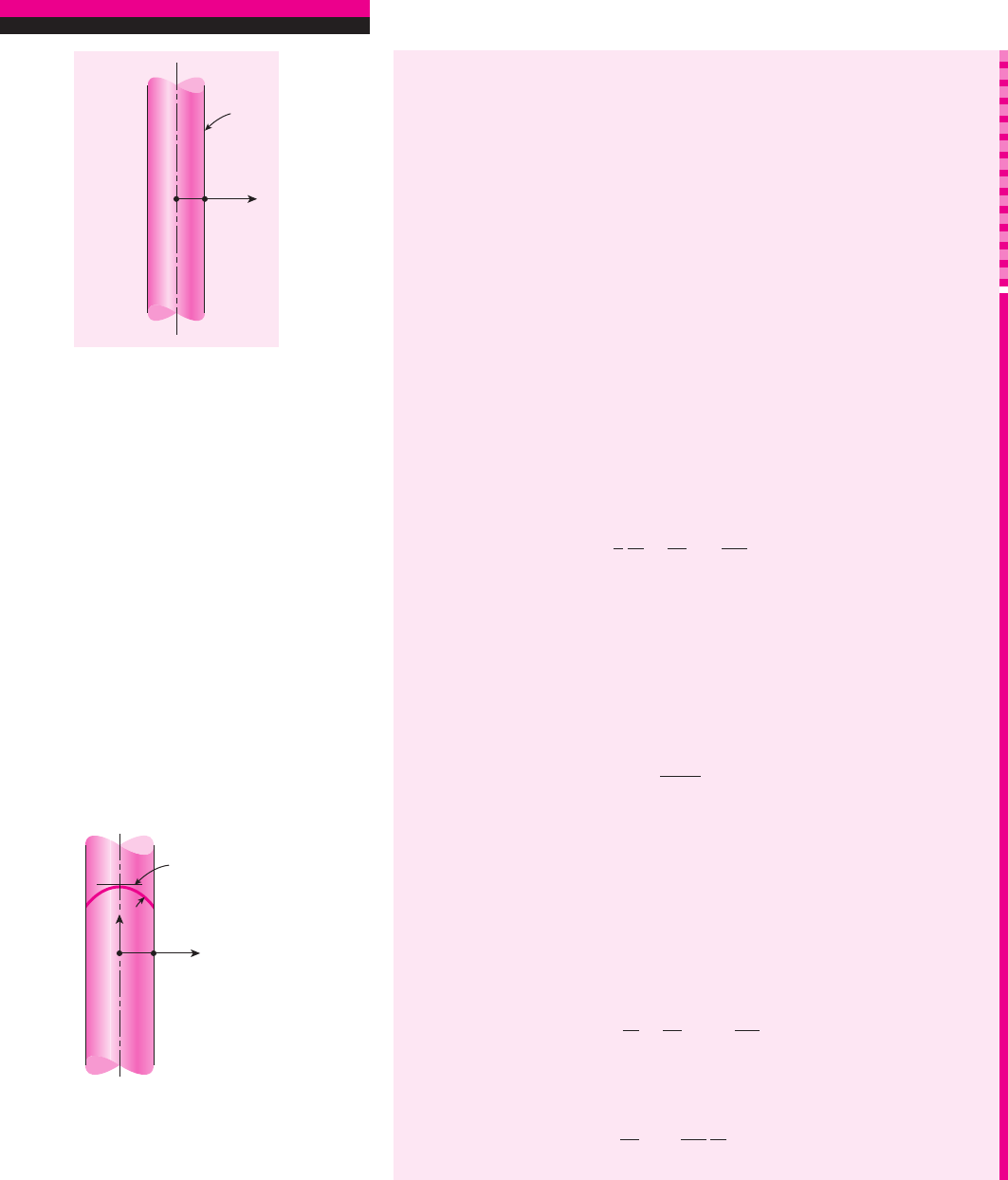
102
HEAT CONDUCTION EQUATION
EXAMPLE 2–17
Variation of Temperature in a Resistance Heater
A long homogeneous resistance wire of radius
r
o
0.2 in and thermal conduc-
tivity
k
7.8 Btu/h·ft·°F is being used to boil water at atmospheric pressure by
the passage of electric current, as shown in Fig. 2–58. Heat is generated in the
wire uniformly as a result of resistance heating at a rate of
e
·
gen
2400
Btu/h·in
3
. If the outer surface temperature of the wire is measured to be
T
s
226°F, obtain a relation for the temperature distribution, and determine the
temperature at the centerline of the wire when steady operating conditions are
reached.
SOLUTION This heat transfer problem is similar to the problem in Exam-
ple 2–16, except that we need to obtain a relation for the variation of tempera-
ture within the wire with
r
. Differential equations are well suited for this purpose.
Assumptions
1 Heat transfer is steady since there is no change with time.
2 Heat transfer is one-dimensional since there is no thermal symmetry about
the centerline and no change in the axial direction. 3 Thermal conductivity is
constant. 4 Heat generation in the wire is uniform.
Properties
The thermal conductivity is given to be
k
7.8 Btu/h·ft·°F.
Analysis
The differential equation which governs the variation of temperature
in the wire is simply Eq. 2–27,
0
This is a second-order linear ordinary differential equation, and thus its general
solution contains two arbitrary constants. The determination of these constants
requires the specification of two boundary conditions, which can be taken to be
T(r
o
) T
s
226°F
and
0
The first boundary condition simply states that the temperature of the outer sur-
face of the wire is 226°F. The second boundary condition is the symmetry con-
dition at the centerline, and states that the maximum temperature in the wire
occurs at the centerline, and thus the slope of the temperature at
r
0 must be
zero (Fig. 2–59). This completes the mathematical formulation of the problem.
Although not immediately obvious, the differential equation is in a form that
can be solved by direct integration. Multiplying both sides of the equation by
r
and rearranging, we obtain
r
Integrating with respect to
r
gives
r C
1
(
a
)
r
2
2
e
.
gen
k
dT
dr
e
.
gen
k
冢
r
dT
dr
冣
d
dr
dT(0)
dr
e
.
gen
k
冢
r
dT
dr
冣
d
dr
1
r
Water 226°F
rr
o
e
gen
·
0
FIGURE 2–58
Schematic for Example 2–17.
r
T
T(r)
r
o
e
gen
·
0
= 0
dT(0)
–——
dr
FIGURE 2–59
The thermal symmetry condition
at the centerline of a wire in which
heat is generated uniformly.
cengel_ch02.qxd 1/5/10 10:47 AM Page 102

103
CHAPTER 2
since the heat generation is constant, and the integral of a derivative of a func-
tion is the function itself. That is, integration removes a derivative. It is conve-
nient at this point to apply the second boundary condition, since it is related to
the first derivative of the temperature, by replacing all occurrences of
r
and
dT
/
dr
in Eq. (
a
) by zero. It yields
0 0 C
1
→ C
1
0
Thus
C
1
cancels from the solution. We now divide Eq. (
a
) by
r
to bring it to a
readily integrable form,
r
Again integrating with respect to
r
gives
T(r) r
2
C
2
(
b
)
We now apply the first boundary condition by replacing all occurrences of
r
by
r
0
and all occurrences of
T
by
T
s
. We get
T
s
C
2
→ C
2
T
s
Substituting this
C
2
relation into Eq. (
b
) and rearranging give
T(r) T
s
( r
2
) (
c
)
which is the desired solution for the temperature distribution in the wire as a
function of
r.
The temperature at the centerline (
r
0) is obtained by replac-
ing
r
in Eq. (
c
) by zero and substituting the known quantities,
T(0) T
s
226°F (0.2 in)
2
263°F
Discussion
The temperature of the centerline is 37°F above the temperature
of the outer surface of the wire. Note that the expression above for the center-
line temperature is identical to Eq. 2–71, which was obtained using an energy
balance on a control volume.
a
12 in
1 ft
b
2400 Btu/hin
3
4 (7.8 Btu/hft °F)
r
2
o
e
.
gen
4k
r
2
o
e
.
gen
4k
r
2
o
e
.
gen
4k
r
2
o
e
.
gen
4k
e
.
gen
4k
e
.
gen
2k
dT
dr
e
.
gen
2k
dT(0)
dr
EXAMPLE 2–18
Heat Conduction in a Two-Layer Medium
Consider a long resistance wire of radius
r
1
0.2 cm and thermal conductiv-
ity
k
wire
15 W/m·K in which heat is generated uniformly as a result of
resistance heating at a constant rate of
e
·
gen
50 W/cm
3
(Fig. 2–60). The wire
is embedded in a 0.5-cm-thick layer of ceramic whose thermal conductivity is
k
ceramic
1.2 W/m·K. If the outer surface temperature of the ceramic layer
is measured to be
T
s
45°C, determine the temperatures at the center of the
resistance wire and the interface of the wire and the ceramic layer under
steady conditions.
Interface
Wire
r
1
r
2
T
s
= 45°C
r
Ceramic layer
FIGURE 2–60
Schematic for Example 2–18.
cengel_ch02.qxd 1/5/10 10:47 AM Page 103

104
HEAT CONDUCTION EQUATION
SOLUTION The surface and interface temperatures of a resistance wire cov-
ered with a ceramic layer are to be determined.
Assumptions
1 Heat transfer is steady since there is no change with time.
2 Heat transfer is one-dimensional since this two-layer heat transfer problem
possesses symmetry about the centerline and involves no change in the axial
direction, and thus
T
T
(
r
). 3 Thermal conductivities are constant. 4 Heat
generation in the wire is uniform.
Properties
It is given that
k
wire
15 W/m·K and
k
ceramic
1.2 W/m·K.
Analysis
Letting
T
I
denote the unknown interface temperature, the heat trans-
fer problem in the wire can be formulated as
0
with
T
wire
(r
1
) T
I
0
This problem was solved in Example 2–17, and its solution was determined
to be
T
wire
(r) T
I
( r
2
) (
a
)
Noting that the ceramic layer does not involve any heat generation and its
outer surface temperature is specified, the heat conduction problem in that
layer can be expressed as
0
with
T
ceramic
(r
1
) T
I
T
ceramic
(r
2
) T
s
45°C
This problem was solved in Example 2–15, and its solution was determined
to be
T
ceramic
(r) (T
s
T
I
) T
I
(
b
)
We have already utilized the first interface condition by setting the wire and ce-
ramic layer temperatures equal to
T
I
at the interface
r
r
1
. The interface tem-
perature
T
I
is determined from the second interface condition that the heat flux
in the wire and the ceramic layer at
r
r
1
must be the same:
k
wire
k
ceramic
→ k
ceramic
Solving for
T
I
and substituting the given values, the interface temperature is
determined to be
冢
1
r
1
冣
T
s
T
I
ln(r
2
/r
1
)
e
.
gen
r
1
2
dT
ceramic
(r
1
)
dr
dT
wire
(r
1
)
dr
ln(r/r
1
)
ln(r
2
/r
1
)
冢
r
dT
ceramic
dr
冣
d
dr
r
2
1
e
.
gen
4k
wire
dT
wire
(0)
dr
e
.
gen
k
冢
r
dT
wire
dr
冣
d
dr
1
r
cengel_ch02.qxd 1/5/10 10:47 AM Page 104

105
CHAPTER 2
T
I
ln T
s
ln 45° C 149.4°C
Knowing the interface temperature, the temperature at the centerline (
r
0)
is obtained by substituting the known quantities into Eq. (
a
),
T
wire
(0) T
I
149.4°C 152.7°C
Thus the temperature of the centerline is slightly above the interface
temperature.
Discussion
This example demonstrates how steady one-dimensional heat con-
duction problems in composite media can be solved. We could also solve this
problem by determining the heat flux at the interface by dividing the total heat
generated in the wire by the surface area of the wire, and then using this value
as the specifed heat flux boundary condition for both the wire and the ceramic
layer. This way the two problems are decoupled and can be solved separately.
(50 10
6
W/m
3
)(0.002 m)
2
4 (15 W/mK)
e
.
gen
r
2
1
4k
wire
0.007 m
0.002 m
(50 10
6
W/m
3
)(0.002 m)
2
2(1.2 W/mK)
r
2
r
1
e
.
gen
r
2
1
2k
ceramic
EXAMPLE 2–19
Heat Conduction in a Plane Wall with Heat
Generation
A large plane wall of thickness 2
L
experiences a uniform heat generation
(Fig. 2–61). Determine the expression for the variation of temperature within
the wall, if (
a
)
T
1
T
2
and (
b
)
T
1
T
2
.
SOLUTION A large plane wall experiences a uniform heat generation. The
expressions for the variation of temperature within the wall for
T
1
T
2
and
T
1
T
2
are to be determined.
Assumptions
1 Heat conduction is steady. 2 Heat conduction is one-dimensional.
3 Thermal conductivity is constant. 4 Heat generation is uniform.
Analysis
We begin with the general heat conduction equation for rectangular
coordinates,
rc
For steady one-dimensional heat conduction and constant thermal conductiv-
ity, the general heat conduction equation is simplified to
Integrating twice gives the general solution to this second order differential
equation as
T(x)
e
#
gen
2k
x
2
C
1
x C
2
d
2
T
dx
2
e
#
gen
k
0
T
t
x
ak
T
x
b
y
ak
T
y
b
z
ak
T
z
b e
#
gen
T
2
+L–L
x
T
1
Plane
wall
FIGURE 2–61
Schematic for Example 2–19.
cengel_ch02.qxd 1/5/10 10:47 AM Page 105

2–7 VARIABLE THERMAL CONDUCTIVITY,
k
(
T
)
You will recall from Chapter 1 that the thermal conductivity of a material, in
general, varies with temperature (Fig. 2–62). However, this variation is mild
for many materials in the range of practical interest and can be disregarded. In
such cases, we can use an average value for the thermal conductivity and treat
it as a constant, as we have been doing so far. This is also common practice for
other temperature-dependent properties such as the density and specific heat.
When the variation of thermal conductivity with temperature in a specified
temperature interval is large, however, it may be necessary to account for this
■
106
HEAT CONDUCTION EQUATION
(
a
) For the case of asymmetrical boundary conditions with
T
1
T
2
, applying
the boundary conditions gives
Note that in this problem the coordinate system is placed at the middle of the
plane wall (x 0) and x to the right of the centerline is considered positive and
to the left negative. In analyzing plane wall problems with heat generation, this
notation is usually adopted in order to better capture the effect of heat gener-
ation on the temperature profile. Solving for the constants
C
1
and
C
2
yields
and
Substituting
C
1
and
C
2
expressions into the general solution, the variation of
temperature within the wall is determined to be
(
a
)
(
b
) For the case of symmetrical boundary conditions, substituting
T
2
T
1
. into
the above equation gives
(
b
)
Discussion
Equation (
a
) shows that the variation of temperature within the
wall for the case of asymmetrical boundary conditions with
T
1
T
2
is not sym-
metric and the maximum temperature occurs to the left of the centerline. Note
that Eq. (a) reduces to the temperature solution of Example 2–10 (Eq. 2–56)
for heat conduction in a plane wall with no heat generation by setting
and making the appropriate coordinate transformation. In the case of symmet-
rical boundary conditions (
T
1
T
2
), Eq. (
b
) shows that the variation of tem-
perature within the wall is symmetric and the maximum temperature occurs at
the centerline. This is comparable to the results shown in Example 2–16 for
temperature variation in a cylindrical resistance heater.
e
#
gen
0
T(x)
e
#
gen
L
2
2k
a1
x
2
L
2
b T
1
T(x)
e
#
gen
L
2
2k
a1
x
2
L
2
b
T
2
T
1
2
a
x
L
b
T
1
T
2
2
C
2
e
#
gen
2k
L
2
T
1
T
2
2
C
1
T
2
T
1
2L
T(L) T
2
e
#
gen
2k
L
2
C
1
L C
2
x L :
T(L) T
1
e
#
gen
2k
L
2
C
1
L C
2
x L :
500
400
300
200
100
50
20
10
5
2
1
100 300 500 1000 2000 4000
Thermal conductivity (W/ m·K)
Temperature (K)
Silver
Copper
Gold
Aluminum
Tungsten
Platinum
Iron
Stainless steel,
AISI 304
Aluminum
oxide
Pyroceram
Fused quartz
FIGURE 2–62
Variation of the thermal conductivity
of some solids with temperature.
cengel_ch02.qxd 1/5/10 10:47 AM Page 106

variation to minimize the error. Accounting for the variation of the thermal
conductivity with temperature, in general, complicates the analysis. But in the
case of simple one-dimensional cases, we can obtain heat transfer relations in
a straightforward manner.
When the variation of thermal conductivity with temperature k(T) is known,
the average value of the thermal conductivity in the temperature range be-
tween T
1
and T
2
can be determined from
k
avg
(2–75)
This relation is based on the requirement that the rate of heat transfer through
a medium with constant average thermal conductivity k
avg
equals the rate of
heat transfer through the same medium with variable conductivity k(T). Note
that in the case of constant thermal conductivity k(T) k, Eq. 2–75 reduces to
k
avg
k, as expected.
Then the rate of steady heat transfer through a plane wall, cylindrical layer,
or spherical layer for the case of variable thermal conductivity can be deter-
mined by replacing the constant thermal conductivity k in Eqs. 2–57, 2–59,
and 2–61 by the k
avg
expression (or value) from Eq. 2–75:
Q
·
plane wall
k
avg
A k(T)dT (2–76)
Q
·
cylinder
2pk
avg
L k(T)dT (2–77)
Q
·
sphere
4pk
avg
r
1
r
2
k(T)dT (2–78)
The variation in thermal conductivity of a material with temperature in the
temperature range of interest can often be approximated as a linear function
and expressed as
k(T) k
0
(1 bT ) (2–79)
where b is called the temperature coefficient of thermal conductivity. The
average value of thermal conductivity in the temperature range T
1
to T
2
in this
case can be determined from
k
avg
k
0
1 b k(T
avg
) (2–80)
Note that the average thermal conductivity in this case is equal to the ther-
mal conductivity value at the average temperature.
We have mentioned earlier that in a plane wall the temperature varies lin-
early during steady one-dimensional heat conduction when the thermal con-
ductivity is constant. But this is no longer the case when the thermal
conductivity changes with temperature, even linearly, as shown in Fig. 2–63.
T
2
T
1
2
冣冢
冮
T
2
T
1
k
0
(1 bT)dT
T
2
T
1
4pr
1
r
2
r
2
r
1
冮
T
1
T
2
T
1
T
2
r
2
r
1
2pL
ln(r
2
/r
1
)
冮
T
1
T
2
T
1
T
2
ln(r
2
/r
1
)
A
L
冮
T
1
T
2
T
1
T
2
L
冮
T
2
T
1
k(T)dT
T
2
T
1
107
CHAPTER 2
0
Plane wall
k(T) = k
0
(1 + bT )
b = 0
b > 0
b < 0
L
T
x
T
1
T
2
FIGURE 2–63
The variation of temperature in a plane
wall during steady one-dimensional
heat conduction for the cases
of constant and variable
thermal conductivity.
cengel_ch02.qxd 1/5/10 10:47 AM Page 107

108
HEAT CONDUCTION EQUATION
EXAMPLE 2–20
Variation of Temperature in a Wall with
k
(
T
)
Consider a plane wall of thickness
L
whose thermal conductivity varies linearly in
a specified temperature range as
k
(
T
)
k
0
(1 b
T
) where
k
0
and b are con-
stants. The wall surface at
x
0 is maintained at a constant temperature of
T
1
while the surface at
x
L
is maintained at
T
2
, as shown in Fig. 2–64. Assuming
steady one-dimensional heat transfer, obtain a relation for (
a
) the heat transfer
rate through the wall and (
b
) the temperature distribution
T
(
x
) in the wall.
SOLUTION A plate with variable conductivity is subjected to specified tem-
peratures on both sides. The variation of temperature and the rate of heat
transfer are to be determined.
Assumptions
1 Heat transfer is given to be steady and one-dimensional.
2 Thermal conductivity varies linearly. 3 There is no heat generation.
Properties
The thermal conductivity is given to be
k
(
T
)
k
0
(1 b
T
).
Analysis
(
a
) The rate of heat transfer through the wall can be determined from
Q
·
k
avg
A
where
A
is the heat conduction area of the wall and
k
avg
k(T
avg
) k
0
1 b
is the average thermal conductivity (Eq. 2–80).
(
b
) To determine the temperature distribution in the wall, we begin with Fourier’s
law of heat conduction, expressed as
Q
·
k(T) A
where the rate of conduction heat transfer Q
·
and the area
A
are constant. Sep-
arating variables and integrating from
x
0 where
T
(0)
T
1
to any
x
where
T
(
x
)
T
, we get
Q
·
dx A k(T)dT
Substituting
k
(
T
)
k
0
(1 b
T
) and performing the integrations we obtain
Q
·
x Ak
0
[(T T
1
) b(T
2
)/2]
Substituting the Q
·
expression from part (
a
) and rearranging give
T
2
T (T
1
T
2
) T
1
0
which is a
quadratic
equation in the unknown temperature
T
. Using the qua-
dratic formula, the temperature distribution
T
(
x
) in the wall is determined to be
T(x)
Discussion
The proper sign of the square root term ( or ) is determined
from the requirement that the temperature at any point within the medium
must remain between
T
1
and
T
2
. This result explains why the temperature dis-
tribution in a plane wall is no longer a straight line when the thermal conduc-
tivity varies with temperature.
B
1
b
2
2k
avg
bk
0
x
L
(T
1
T
2
) T
2
1
2
b
T
1
1
b
2
b
T
2
1
x
L
2k
avg
bk
0
2
b
T
2
1
冕
T
T
1
冕
x
0
dT
dx
T
2
T
1
2
冣冢
T
1
T
2
L
0
Plane
wall
k(T ) = k
0
(1 + bT )
L
x
T
2
T
1
FIGURE 2–64
Schematic for Example 2–20.
cengel_ch02.qxd 1/5/10 10:47 AM Page 108

109
CHAPTER 2
EXAMPLE 2–21
Heat Conduction through a Wall with
k
(
T
)
Consider a 2-m-high and 0.7-m-wide bronze plate whose thickness is 0.1 m.
One side of the plate is maintained at a constant temperature of 600 K while
the other side is maintained at 400 K, as shown in Fig. 2–65. The thermal
conductivity of the bronze plate can be assumed to vary linearly in that tem-
perature range as
k
(
T
)
k
0
(1 b
T
) where
k
0
38 W/m·K and b 9.21
10
4
K
1
. Disregarding the edge effects and assuming steady one-dimensional
heat transfer, determine the rate of heat conduction through the plate.
SOLUTION A plate with variable conductivity is subjected to specified tem-
peratures on both sides. The rate of heat transfer is to be determined.
Assumptions
1 Heat transfer is given to be steady and one-dimensional.
2 Thermal conductivity varies linearly. 3 There is no heat generation.
Properties
The thermal conductivity is given to be
k
(
T
)
k
0
(1 b
T
).
Analysis
The average thermal conductivity of the medium in this case is sim-
ply the value at the average temperature and is determined from
k
avg
k(T
avg
) k
0
1 b
(38 W/m·K) 1 (9.21 10
4
K
1
)
55.5 W/m·K
Then the rate of heat conduction through the plate can be determined from
Eq. 2–76 to be
Q
·
k
avg
A
(55.5 W/m·K)(2 m 0.7 m) 155 kW
Discussion
We would have obtained the same result by substituting the given
k
(
T
) relation into the second part of Eq. 2–76 and performing the indicated in-
tegration.
(600 400)K
0.1 m
T
1
T
2
L
(600 400) K
2
冥冤
T
2
T
1
2
冣冢
Bronze
plate
k(T ) = k
0
(1 + bT )
T
2
= 400 KT
1
= 600 K
Q
·
L
FIGURE 2–65
Schematic for Example 2–21.
TOPIC OF SPECIAL INTEREST*
A Brief Review of Differential Equations
As we mentioned in Chapter 1, the description of most scientific problems
involves relations that involve changes in some key variables with respect
to each other. Usually the smaller the increment chosen in the changing
variables, the more general and accurate the description. In the limiting
case of infinitesimal or differential changes in variables, we obtain
differential equations, which provide precise mathematical formulations
for the physical principles and laws by representing the rates of change as
*This section can be skipped without a loss of continuity.
cengel_ch02.qxd 1/7/10 9:54 AM Page 109

110
INTRODUCTION AND BASIC CONCEPTS
derivatives. Therefore, differential equations are used to investigate a wide
variety of problems in sciences and engineering, including heat transfer.
Differential equations arise when relevant physical laws and principles
are applied to a problem by considering infinitesimal changes in the vari-
ables of interest. Therefore, obtaining the governing differential equation
for a specific problem requires an adequate knowledge of the nature of the
problem, the variables involved, appropriate simplifying assumptions, and
the applicable physical laws and principles involved, as well as a careful
analysis.
An equation, in general, may involve one or more variables. As the name
implies, a variable is a quantity that may assume various values during a
study. A quantity whose value is fixed during a study is called a constant.
Constants are usually denoted by the earlier letters of the alphabet such as
a, b, c, and d, whereas variables are usually denoted by the later ones such
as t, x, y, and z. A variable whose value can be changed arbitrarily is called
an independent variable (or argument). A variable whose value depends
on the value of other variables and thus cannot be varied independently is
called a dependent variable (or a function).
A dependent variable y that depends on a variable x is usually denoted as
y(x) for clarity. However, this notation becomes very inconvenient and
cumbersome when y is repeated several times in an expression. In such
cases it is desirable to denote y(x) simply as y when it is clear that y is a
function of x. This shortcut in notation improves the appearance and the
readability of the equations. The value of y at a fixed number a is denoted
by y(a).
The derivative of a function y(x) at a point is equivalent to the slope of
the tangent line to the graph of the function at that point and is defined as
(Fig. 2–66)
y(x) (2–81)
Here x represents a (small) change in the independent variable x and is
called an increment of x. The corresponding change in the function y is
called an increment of y and is denoted by y. Therefore, the derivative of
a function can be viewed as the ratio of the increment y of the function to
the increment x of the independent variable for very small x. Note that
y and thus y(x) are zero if the function y does not change with x.
Most problems encountered in practice involve quantities that change
with time t, and their first derivatives with respect to time represent the rate
of change of those quantities with time. For example, if N(t) denotes the
population of a bacteria colony at time t, then the first derivative N
dN/dt represents the rate of change of the population, which is the amount
the population increases or decreases per unit time.
The derivative of the first derivative of a function y is called the second
derivative of y, and is denoted by y or d
2
y/dx
2
. In general, the derivative of
the (n 1)st derivative of y is called the nth derivative of y and is denoted
by y
(n)
or d
n
y/dx
n
. Here, n is a positive integer and is called the order of the
y(x x) y(x)
x
lim
x → 0
y
x
lim
x → 0
dy(x)
dx
y
(x + Δx)
x + Δxx
Δx
y(x)
y(x)
Tangent line
y
x
Δy
FIGURE 2–66
The derivative of a function at a point
represents the slope of the tangent
line of the function at that point.
cengel_ch02.qxd 1/5/10 10:47 AM Page 110

CHAPTER 2
111
derivative. The order n should not be confused with the degree of a deriva-
tive. For example, y is the third-order derivative of y, but (y)
3
is the third
degree of the first derivative of y. Note that the first derivative of a function
represents the slope or the rate of change of the function with the indepen-
dent variable, and the second derivative represents the rate of change of the
slope of the function with the independent variable.
When a function y depends on two or more independent variables such as
x and t, it is sometimes of interest to examine the dependence of the function
on one of the variables only. This is done by taking the derivative of the
function with respect to that variable while holding the other variables con-
stant. Such derivatives are called partial derivatives. The first partial
derivatives of the function y(x, t) with respect to x and t are defined as
(Fig. 2–67)
(2–82)
(2–83)
Note that when finding y/x we treat t as a constant and differentiate y
with respect to x. Likewise, when finding y/t we treat x as a constant and
differentiate y with respect to t.
Integration can be viewed as the inverse process of differentiation. Inte-
gration is commonly used in solving differential equations since solving a
differential equation is essentially a process of removing the derivatives
from the equation. Differentiation is the process of finding y(x) when a
function y(x) is given, whereas integration is the process of finding the
function y(x) when its derivative y(x) is given. The integral of this deriva-
tive is expressed as
y(x)dx dy y(x) C (2–84)
since y(x)dx dy and the integral of the differential of a function is the
function itself (plus a constant, of course). In Eq. 2–84, x is the integration
variable and C is an arbitrary constant called the integration constant.
The derivative of y(x) C is y(x) no matter what the value of the con-
stant C is. Therefore, two functions that differ by a constant have the same
derivative, and we always add a constant C during integration to recover
this constant that is lost during differentiation. The integral in Eq. 2–84 is
called an indefinite integral since the value of the arbitrary constant C is
indefinite. The described procedure can be extended to higher-order deriv-
atives (Fig. 2–68). For example,
y(x)dx y(x) C (2–85)
This can be proved by defining a new variable u(x) y(x), differentiating
it to obtain u(x) y(x), and then applying Eq. 2–84. Therefore, the order
of a derivative decreases by one each time it is integrated.
冕
冕冕
y(x, t t) y(x, t)
t
lim
t → 0
y
t
y(x x, t) y(x, t)
x
lim
x → 0
y
x
x
y
z
∂z
∂x
()
y
FIGURE 2–67
Graphical representation
of partial derivative z/x.
dy = y + C
∫
y′dx = y + C
∫
y″dx = y′ + C
∫
y″′dx = y″ + C
∫
y
(n)
dx = y
(n – 1)
+ C
∫
FIGURE 2–68
Some indefinite integrals
that involve derivatives.
cengel_ch02.qxd 1/5/10 10:47 AM Page 111

112
INTRODUCTION AND BASIC CONCEPTS
Classification of Differential Equations
A differential equation that involves only ordinary derivatives is called an
ordinary differential equation, and a differential equation that involves
partial derivatives is called a partial differential equation. Then it follows
that problems that involve a single independent variable result in ordinary
differential equations, and problems that involve two or more independent
variables result in partial differential equations. A differential equation may
involve several derivatives of various orders of an unknown function. The
order of the highest derivative in a differential equation is the order of the
equation. For example, the order of y (y)
4
7x
5
is 3 since it contains
no fourth or higher order derivatives.
You will remember from algebra that the equation 3x 5 0 is much
easier to solve than the equation x
4
3x 5 0 because the first equa-
tion is linear whereas the second one is nonlinear. This is also true for dif-
ferential equations. Therefore, before we start solving a differential
equation, we usually check for linearity. A differential equation is said to
be linear if the dependent variable and all of its derivatives are of the first
degree and their coefficients depend on the independent variable only. In
other words, a differential equation is linear if it can be written in a form
that does not involve (1) any powers of the dependent variable or its deriv-
atives such as y
3
or (y)
2
, (2) any products of the dependent variable or its
derivatives such as yy or yy , and (3) any other nonlinear functions of the
dependent variable such as sin y or e
y
. If any of these conditions apply, it is
nonlinear (Fig. 2–69).
A linear differential equation, however, may contain (1) powers or
nonlinear functions of the independent variable, such as x
2
and cos x
and (2) products of the dependent variable (or its derivatives) and func-
tions of the independent variable, such as x
3
y, x
2
y, and e
2x
y. A linear
differential equation of order n can be expressed in the most general
form as
y
(n)
f
1
(x)y
(n 1)
· · · f
n–1
(x)yf
n
(x)y R(x) (2–86)
A differential equation that cannot be put into this form is nonlinear. A
linear differential equation in y is said to be homogeneous as well if
R(x) 0. Otherwise, it is nonhomogeneous. That is, each term in a linear
homogeneous equation contains the dependent variable or one of its deriv-
atives after the equation is cleared of any common factors. The term R(x) is
called the nonhomogeneous term.
Differential equations are also classified by the nature of the coefficients
of the dependent variable and its derivatives. A differential equation is said
to have constant coefficients if the coefficients of all the terms that involve
the dependent variable or its derivatives are constants. If, after clearing any
common factors, any of the terms with the dependent variable or its deriv-
atives involve the independent variable as a coefficient, that equation is said
to have variable coefficients (Fig. 2–70). Differential equations with
(a) A nonlinear equation:
3(y″)
2
– 4yy′ + e
2xy
= 6x
2
(b) A linear equation:
3x
2
y″ – 4xy′ + e
2x
y = 6x
2
Power Product
Other
nonlinear
functions
FIGURE 2–69
A differential equation that is
(a) nonlinear and (b) linear. When
checking for linearity, we examine
the dependent variable only.
(a) With constant coefficients:
y″ + 6y ′ – 2y = xe
–2x
(b) With variable coefficients:
Constant
Variable
y″ – 6x
2
y′ –
y = xe
–2x
2
x – 1
FIGURE 2–70
A differential equation with
(a) constant coefficients and
(b) variable coefficients.
cengel_ch02.qxd 1/5/10 10:47 AM Page 112

CHAPTER 2
113
constant coefficients are usually much easier to solve than those with vari-
able coefficients.
Solutions of Differential Equations
Solving a differential equation can be as easy as performing one or
more integrations; but such simple differential equations are usually the
exception rather than the rule. There is no single general solution method
applicable to all differential equations. There are different solution tech-
niques, each being applicable to different classes of differential equations.
Sometimes solving a differential equation requires the use of two or more
techniques as well as ingenuity and mastery of solution methods. Some dif-
ferential equations can be solved only by using some very clever tricks.
Some cannot be solved analytically at all.
In algebra, we usually seek discrete values that satisfy an algebraic equa-
tion such as x
2
7x 10 0. When dealing with differential equations,
however, we seek functions that satisfy the equation in a specified interval.
For example, the algebraic equation x
2
7x 10 0 is satisfied by two
numbers only: 2 and 5. But the differential equation y7y 0 is satis-
fied by the function e
7x
for any value of x (Fig. 2–71).
Consider the algebraic equation x
3
6x
2
11x 6 0. Obviously,
x 1 satisfies this equation, and thus it is a solution. However, it is not
the only solution of this equation. We can easily show by direct substitu-
tion that x 2 and x 3 also satisfy this equation, and thus they are so-
lutions as well. But there are no other solutions to this equation. Therefore,
we say that the set 1, 2, and 3 forms the complete solution to this algebraic
equation.
The same line of reasoning also applies to differential equations. Typi-
cally, differential equations have multiple solutions that contain at least one
arbitrary constant. Any function that satisfies the differential equation on an
interval is called a solution of that differential equation in that interval. A
solution that involves one or more arbitrary constants represents a family of
functions that satisfy the differential equation and is called a general solu-
tion of that equation. Not surprisingly, a differential equation may have
more than one general solution. A general solution is usually referred to as
the general solution or the complete solution if every solution of the
equation can be obtained from it as a special case. A solution that can be
obtained from a general solution by assigning particular values to the arbi-
trary constants is called a specific solution.
You will recall from algebra that a number is a solution of an algebraic
equation if it satisfies the equation. For example, 2 is a solution of the equa-
tion x
3
8 0 because the substitution of 2 for x yields identically zero.
Likewise, a function is a solution of a differential equation if that function
satisfies the differential equation. In other words, a solution function yields
identity when substituted into the differential equation. For example, it can
be shown by direct substitution that the function 3e
2x
is a solution of y
4y 0 (Fig. 2–72).
(a) An algebraic equation:
y
2
– 7y – 10 = 0
Solution: y = 2 and y = 5
(b) A differential equation:
y′ – 7y = 0
Solution: y = e
7x
FIGURE 2–71
Unlike those of algebraic equations,
the solutions of differential equations
are typically functions instead
of discrete values.
Function: f = 3e
–2x
Differential equation: y″ – 4y = 0
Derivatives of f:
f ′ = –6e
–2x
f ″ = 12e
–2x
Substituting into y″ – 4y = 0:
f ″ – 4f
=
0
12e
–2x
– 4 × 3e
–2x
=
0
0 = 0
Therefore, the function 3e
–2x
is a solution
of the differential equation y″ – 4y = 0.
?
?
FIGURE 2–72
Verifying that a given function is a
solution of a differential equation.
cengel_ch02.qxd 1/5/10 10:47 AM Page 113

In this chapter we have studied the heat conduction equation and
its solutions. Heat conduction in a medium is said to be steady
when the temperature does not vary with time and unsteady or
transient when it does. Heat conduction in a medium is said to
be one-dimensional when conduction is significant in one di-
mension only and negligible in the other two dimensions. It is
said to be two-dimensional when conduction in the third dimen-
sion is negligible and three-dimensional when conduction in all
dimensions is significant. In heat transfer analysis, the conver-
sion of electrical, chemical, or nuclear energy into heat (or ther-
mal) energy is characterized as heat generation.
The heat conduction equation can be derived by performing
an energy balance on a differential volume element. The one-
dimensional heat conduction equation in rectangular, cylindri-
cal, and spherical coordinate systems for the case of constant
thermal conductivities are expressed as
where the property a k/rc is the thermal diffusivity of the
material.
The solution of a heat conduction problem depends on the
conditions at the surfaces, and the mathematical expressions
for the thermal conditions at the boundaries are called the
boundary conditions. The solution of transient heat conduction
problems also depends on the condition of the medium at the
beginning of the heat conduction process. Such a condition,
which is usually specified at time t 0, is called the initial
condition, which is a mathematical expression for the tempera-
ture distribution of the medium initially. Complete mathemati-
cal description of a heat conduction problem requires the
specification of two boundary conditions for each dimension
along which heat conduction is significant, and an initial con-
dition when the problem is transient. The most common
boundary conditions are the specified temperature, specified
heat flux, convection, and radiation boundary conditions. A
boundary surface, in general, may involve specified heat flux,
convection, and radiation at the same time.
For steady one-dimensional heat transfer through a plate of
thickness L, the various types of boundary conditions at the
surfaces at x 0 and x L can be expressed as
Specified temperature:
T(0) T
1
and T(L) T
2
where T
1
and T
2
are the specified temperatures at surfaces at
x 0 and x L.
T
t
1
e
.
gen
k
冢
r
2
T
r
冣
r
1
r
2
T
t
1
e
.
gen
k
冢
r
T
r
冣
r
1
r
T
t
1
e
.
gen
k
2
T
x
2
114
HEAT CONDUCTION EQUATION
Specified heat flux:
k q
·
0
and k q
·
L
where q
·
0
and q
·
L
are the specified heat fluxes at surfaces at
x 0 and x L.
Insulation or thermal symmetry:
0 and 0
Convection:
k h
1
[T
1
T(0)] and k h
2
[T(L) T
2
]
where h
1
and h
2
are the convection heat transfer coefficients
and T
1
and T
2
are the temperatures of the surrounding medi-
ums on the two sides of the plate.
Radiation:
k e
1
s[T
4
surr, 1
T(0)
4
] and
k e
2
s[T(L)
4
T
4
surr, 2
]
where e
1
and e
2
are the emissivities of the boundary surfaces,
s 5.67 10
8
W/m
2
·K
4
is the Stefan–Boltzmann constant,
and T
surr, 1
and T
surr, 2
are the average temperatures of the sur-
faces surrounding the two sides of the plate. In radiation calcu-
lations, the temperatures must be in K or R.
Interface of two bodies A and B in perfect contact at x x
0
:
T
A
(x
0
) T
B
(x
0
) and k
A
k
B
where k
A
and k
B
are the thermal conductivities of the layers
A and B.
Heat generation is usually expressed per unit volume of the
medium and is denoted by
e
·
gen
, whose unit is W/m
3
. Under
steady conditions, the surface temperature T
s
of a plane wall
of thickness 2L, a cylinder of outer radius r
o
, and a sphere
of radius r
o
in which heat is generated at a constant rate of
dT
B
(x
0
)
dx
dT
A
(x
0
)
dx
dT(L)
dx
dT(0)
dx
dT(L)
dx
dT(0)
dx
dT(L)
dx
dT(0)
dx
dT(L)
dx
dT(0)
dx
SUMMARY
cengel_ch02.qxd 1/5/10 10:48 AM Page 114

CHAPTER 2
115
e
·
gen
per unit volume in a surrounding medium at T
can be
expressed as
T
s, plane wall
T
T
s, cylinder
T
T
s, sphere
T
where h is the convection heat transfer coefficient. The maxi-
mum temperature rise between the surface and the midsection
of a medium is given by
T
max, plane wall
T
max, cylinder
T
max, sphere
When the variation of thermal conductivity with temperature
k(T) is known, the average value of the thermal conductivity in
the temperature range between T
1
and T
2
can be determined from
e
.
gen
r
2
o
6k
e
.
gen
r
2
o
4k
e
.
gen
L
2
2k
e
.
gen
r
o
3h
e
.
gen
r
o
2h
e
.
gen
L
h
k
avg
Then the rate of steady heat transfer through a plane wall,
cylindrical layer, or spherical layer can be expressed as
Q
·
plane wall
k
avg
A k(T)dT
Q
·
cylinder
2pk
avg
L k(T )dT
Q
·
sphere
4pk
avg
r
1
r
2
k(T )dT
The variation of thermal conductivity of a material with tem-
perature can often be approximated as a linear function and
expressed as
k(T) k
0
(1 bT)
where b is called the temperature coefficient of thermal
conductivity.
4r
1
r
2
r
2
r
1
冕
T
1
T
2
T
1
T
2
r
2
r
1
2pL
ln(r
2
/r
1
)
冮
T
1
T
2
T
1
T
2
ln(r
2
/r
1
)
A
L
冕
T
1
T
2
T
1
T
2
L
冮
T
2
T
1
k(T )dT
T
2
T
1
1. W. E. Boyce and R. C. Diprima. Elementary Differential
Equations and Boundary Value Problems. 4th ed.
New York: John Wiley & Sons, 1986.
2. S. S. Kutateladze. Fundamentals of Heat Transfer. New
York: Academic Press, 1963.
REFERENCES AND SUGGESTED READING
Introduction
2–1C Is heat transfer a scalar or vector quantity? Explain.
Answer the same question for temperature.
2–2C In order to size the compressor of a new refrigerator, it
is desired to determine the rate of heat transfer from the kitchen
air into the refrigerated space through the walls, door, and the
top and bottom section of the refrigerator. In your analysis,
would you treat this as a transient or steady-state heat transfer
problem? Also, would you consider the heat transfer to be one-
dimensional or multidimensional? Explain.
2–3C How does transient heat transfer differ from steady
heat transfer? How does one-dimensional heat transfer differ
from two-dimensional heat transfer?
2–4C In order to determine the size of the heating element of
a new oven, it is desired to determine the rate of heat loss
through the walls, door, and the top and bottom section of the
oven. In your analysis, would you consider this to be a steady
or transient heat transfer problem? Also, would you consider
the heat transfer to be one-dimensional or multidimensional?
Explain.
2–5C Consider a round potato being baked in an oven. Would
you model the heat transfer to the potato as one-, two-, or
PROBLEMS*
*Problems designated by a “C” are concept questions, and
students are encouraged to answer them all. Problems designated
by an “E” are in English units, and the SI users can ignore them.
Problems with the icon are solved using EES, and the complete
solutions together with parametric studies are included on the
enclosed DVD. Problems with the icon are comprehensive in
nature, and are intended to be solved with a computer, preferably
using the EES software that accompanies this text.
cengel_ch02.qxd 1/5/10 10:48 AM Page 115

three-dimensional? Would the heat transfer be steady or tran-
sient? Also, which coordinate system would you use to solve
this problem, and where would you place the origin? Explain.
2–6C Consider an egg being cooked in boiling water in a pan.
Would you model the heat transfer to the egg as one-, two-, or
three-dimensional? Would the heat transfer be steady or tran-
sient? Also, which coordinate system would you use to solve this
problem, and where would you place the origin? Explain.
2–7C Consider a hot dog being cooked in boiling water in a
pan. Would you model the heat transfer to the hot dog as one-,
two-, or three-dimensional? Would the heat transfer be steady or
transient? Also, which coordinate system would you use to solve
this problem, and where would you place the origin? Explain.
116
HEAT CONDUCTION EQUATION
2–15 Heat flux meters use a very sensitive device known as a
thermopile to measure the temperature difference across a thin,
heat conducting film made of kapton (k 0.345 W/m·K). If
the thermopile can detect temperature differences of 0.1°C or
more and the film thickness is 2 mm, what is the minimum heat
flux this meter can detect?
Answer:
17.3 W/m
2
2–16 In a nuclear reactor, heat is generated uniformly in the
5-cm-diameter cylindrical uranium rods at a rate of 2 10
8
W/m
3
. If the length of the rods is 1 m, determine the rate of
heat generation in each rod.
Answer:
393 kW
2–17 In a solar pond, the absorption of solar energy can
be modeled as heat generation and can be approximated by
e
·
gen
e
·
0
e
bx
, where e
·
0
is the rate of heat absorption at the
top surface per unit volume and b is a constant. Obtain a rela-
tion for the total rate of heat generation in a water layer of sur-
face area A and thickness L at the top of the pond.
FIGURE P2–7C
Hot dog
Boiling water
2–8C Consider the cooking process of a roast beef in an
oven. Would you consider this to be a steady or transient heat
transfer problem? Also, would you consider this to be one-,
two-, or three-dimensional? Explain.
2–9C Consider heat loss from a 200-L cylindrical hot water
tank in a house to the surrounding medium. Would you consider
this to be a steady or transient heat transfer problem? Also,
would you consider this heat transfer problem to be one-, two-,
or three-dimensional? Explain.
2–10C Does a heat flux vector at a point P on an isothermal
surface of a medium have to be perpendicular to the surface at
that point? Explain.
2–11C From a heat transfer point of view, what is the differ-
ence between isotropic and unisotropic materials?
2–12C What is heat generation in a solid? Give examples.
2–13C Heat generation is also referred to as energy genera-
tion or thermal energy generation. What do you think of these
phrases?
2–14C Consider a cold canned drink left on a dinner table.
Would you model the heat transfer to the drink as one-, two-, or
three-dimensional? Would the heat transfer be steady or tran-
sient? Also, which coordinate system would you use to analyze
this heat transfer problem, and where would you place the ori-
gin? Explain.
FIGURE P2–17
0
L
x
Solar
energy
Solar
pond
Radiation
beam being
absorbed
2–18 Consider a large 3-cm-thick stainless steel plate in
which heat is generated uniformly at a rate of 5 10
6
W/m
3
.
Assuming the plate is losing heat from both sides, determine
the heat flux on the surface of the plate during steady opera-
tion.
Answer:
75 kW/m
2
2–19E The resistance wire of a 800-W iron is 15 in long and
has a diameter of D 0.08 in. Determine the rate of heat gen-
eration in the wire per unit volume, in Btu/h·ft
3
, and the heat
flux on the outer surface of the wire, in Btu/h·ft
2
, as a result of
this heat generation.
FIGURE P2-19E
q
e
gen
·
D
·
2–20E Reconsider Prob. 2-19E. Using EES (or other)
software, evaluate and plot the surface heat flux
as a function of wire diameter as the diameter varies from
0.02 to 0.40 in. Discuss the results.
cengel_ch02.qxd 1/5/10 10:48 AM Page 116

CHAPTER 2
117
Heat Conduction Equation
2–21C Write down the one-dimensional transient heat con-
duction equation for a plane wall with constant thermal con-
ductivity and heat generation in its simplest form, and indicate
what each variable represents.
2–22C Write down the one-dimensional transient heat con-
duction equation for a long cylinder with constant thermal con-
ductivity and heat generation, and indicate what each variable
represents.
2–23 Starting with an energy balance on a rectangular vol-
ume element, derive the one-dimensional transient heat con-
duction equation for a plane wall with constant thermal
conductivity and no heat generation.
2–24 Starting with an energy balance on a cylindrical shell
volume element, derive the steady one-dimensional heat con-
duction equation for a long cylinder with constant thermal con-
ductivity in which heat is generated at a rate of
e
·
gen
.
2–26 Consider a medium in which the heat conduction equa-
tion is given in its simplest form as
(a) Is heat transfer steady or transient?
(b) Is heat transfer one-, two-, or three-dimensional?
(c) Is there heat generation in the medium?
(d) Is the thermal conductivity of the medium constant or
variable?
2-27 Consider a medium in which the heat conduction equa-
tion is given in its simplest form as
(a) Is heat transfer steady or transient?
(b) Is heat transfer one-, two-, or three-dimensional?
(c) Is there heat generation in the medium?
(d) Is the thermal conductivity of the medium constant or
variable?
2-28 Consider a medium in which the heat conduction equa-
tion is given in its simplest form as
e
·
gen
0
(a) Is heat transfer steady or transient?
(b) Is heat transfer one-, two-, or three-dimensional?
(c) Is there heat generation in the medium?
(d) Is the thermal conductivity of the medium constant or
variable?
2–29 Consider a medium in which the heat conduction equa-
tion is given in its simplest form as
e
·
gen
0
(a) Is heat transfer steady or transient?
(b) Is heat transfer one-, two-, or three-dimensional?
(c) Is there heat generation in the medium?
(d) Is the thermal conductivity of the medium constant or
variable?
2–30 Consider a medium in which the heat conduction equa-
tion is given in its simplest form as
(a) Is heat transfer steady or transient?
(b) Is heat transfer one-, two-, or three-dimensional?
(c) Is there heat generation in the medium?
(d) Is the thermal conductivity of the medium constant or
variable?
T
t
1
a
冢
r
2
T
r
冣
r
1
r
2
冢
rk
dT
dr
冣
d
dr
1
r
冢
k
T
z
冣
z
冢
kr
T
r
冣
r
1
r
T
t
1
a
2
T
y
2
2
T
x
2
T
t
1
a
2
T
x
2
FIGURE P2–24
0
r + Δr
r
r
L
2–25 Starting with an energy balance on a spherical shell
volume element, derive the one-dimensional transient heat
conduction equation for a sphere with constant thermal con-
ductivity and no heat generation.
FIGURE P2–25
0
R
rr
r + Δr
cengel_ch02.qxd 1/5/10 10:48 AM Page 117

2–31 Consider a medium in which the heat conduction equa-
tion is given in its simplest form as
r 0
(a) Is heat transfer steady or transient?
(b) Is heat transfer one-, two-, or three-dimensional?
(c) Is there heat generation in the medium?
(d) Is the thermal conductivity of the medium constant or
variable?
2–32 Starting with an energy balance on a volume element,
derive the two-dimensional transient heat conduction equation
in rectangular coordinates for T(x, y, t) for the case of constant
thermal conductivity and no heat generation.
2–33 Starting with an energy balance on a ring-shaped vol-
ume element, derive the two-dimensional steady heat conduc-
tion equation in cylindrical coordinates for T(r, z) for the case
of constant thermal conductivity and no heat generation.
dT
dr
d
2
T
dr
2
118
HEAT CONDUCTION EQUATION
(a) Is heat transfer steady or transient?
(b) Is heat transfer one-, two-, or three-dimensional?
(c) Is there heat generation in the medium?
(d) Is the thermal conductivity of the medium constant or
variable?
Boundary and Initial Conditions;
Formulation of Heat Conduction Problems
2–36C What is a boundary condition? How many boundary
conditions do we need to specify for a two-dimensional heat
conduction problem?
2–37C What is an initial condition? How many initial condi-
tions do we need to specify for a two-dimensional heat
conduction problem?
2–38C What is a thermal symmetry boundary condition?
How is it expressed mathematically?
2–39C How is the boundary condition on an insulated sur-
face expressed mathematically?
2–40C It is claimed that the temperature profile in a medium
must be perpendicular to an insulated surface. Is this a valid
claim? Explain.
2–41C Why do we try to avoid the radiation boundary condi-
tions in heat transfer analysis?
2–42 Consider an aluminum pan used to cook stew on top of
an electric range. The bottom section of the pan is L 0.25 cm
thick and has a diameter of D 18 cm. The electric heating unit
on the range top consumes 900 W of power during cooking, and
90 percent of the heat generated in the heating element is trans-
ferred to the pan. During steady operation, the temperature of the
inner surface of the pan is measured to be 108°C. Assuming tem-
perature-dependent thermal conductivity and one-dimensional
heat transfer, express the mathematical formulation (the differen-
tial equation and the boundary conditions) of this heat conduc-
tion problem during steady operation. Do not solve.
2–43 Consider a spherical container of inner radius r
1
, outer
radius r
2
, and thermal conductivity k. Express the boundary
condition on the inner surface of the container for steady one-
dimensional conduction for the following cases: (a) specified
temperature of 50°C, (b) specified heat flux of 45 W/m
2
toward
the center, (c) convection to a medium at T
with a heat trans-
fer coefficient of h.
FIGURE P2–33
Δz
r + Δr
r
r
2–34 Starting with an energy balance on a disk volume ele-
ment, derive the one-dimensional transient heat conduction
equation for T(z, t) in a cylinder of diameter D with an insu-
lated side surface for the case of constant thermal conductivity
with heat generation.
e
gen
·
z
Disk
0
Insulation
A = constan
t
z + Δz
z
FIGURE P2–34
2–35 Consider a medium in which the heat conduction equa-
tion is given in its simplest form as
T
t
1
a
2
T
f
2
1
r
2
sin
2
u
ar
2
T
r
b
r
1
r
2
FIGURE P2–43
r
1
Spherical container
r
2
r
cengel_ch02.qxd 1/5/10 10:48 AM Page 118

CHAPTER 2
119
2–44 Heat is generated in a long wire of radius r
o
at a con-
stant rate of e
·
gen
per unit volume. The wire is covered with a
plastic insulation layer. Express the heat flux boundary condi-
tion at the interface in terms of the heat generated.
2–45 Consider a long pipe of inner radius r
1
, outer radius r
2
,
and thermal conductivity k. The outer surface of the pipe is
subjected to convection to a medium at T
with a heat transfer
coefficient of h, but the direction of heat transfer is not known.
Express the convection boundary condition on the outer sur-
face of the pipe.
2–46 Consider a spherical shell of inner radius r
1
, outer ra-
dius r
2
, thermal conductivity k, and emissivitye. The outer sur-
face of the shell is subjected to radiation to surrounding
surfaces at T
surr
, but the direction of heat transfer is not known.
Express the radiation boundary condition on the outer surface
of the shell.
2–47 A container consists of two spherical layers, A and B,
that are in perfect contact. If the radius of the interface is r
o
,ex-
press the boundary conditions at the interface.
2–48 Consider a steel pan used to boil water on top of an
electric range. The bottom section of the pan is L 0.3 cm
thick and has a diameter of D 20 cm. The electric heating
unit on the range top consumes 1250 W of power during cook-
ing, and 85 percent of the heat generated in the heating element
is transferred uniformly to the pan. Heat transfer from the top
surface of the bottom section to the water is by convection with
a heat transfer coefficient of h. Assuming constant thermal
conductivity and one-dimensional heat transfer, express the
mathematical formulation (the differential equation and the
boundary conditions) of this heat conduction problem during
steady operation. Do not solve.
convection and radiation. The interior of the house is main-
tained at T
1
, while the ambient air temperature outside re-
mains at T
2
. The sky, the ground, and the surfaces of the
surrounding structures at this location can be modeled as a sur-
face at an effective temperature of T
sky
for radiation exchange
on the outer surface. The radiation exchange between the inner
surface of the wall and the surfaces of the walls, floor, and ceil-
ing it faces is negligible. The convection heat transfer coeffi-
cients on the inner and outer surfaces of the wall are h
1
and h
2
,
respectively. The thermal conductivity of the wall material is k
and the emissivity of the outer surface is e
2
. Assuming the heat
transfer through the wall to be steady and one-dimensional, ex-
press the mathematical formulation (the differential equation
and the boundary and initial conditions) of this heat conduction
problem. Do not solve.
FIGURE P2–48
Steel pan
0
Water
L
x
2–49E A 2-kW resistance heater wire whose thermal con-
ductivity is k 10.4 Btu/h·ft·R has a radius of r
o
0.06 in. and
a length of L 15 in, and is used for space heating. Assuming
constant thermal conductivity and one-dimensional heat trans-
fer, express the mathematical formulation (the differential
equation and the boundary conditions) of this heat conduction
problem during steady operation. Do not solve.
2–50 Consider the East wall of a house that has a thickness of
L. The outer surface of the wall exchanges heat by both
FIGURE P2–50
T
sky
h
1
T
⬁1
h
2
T
⬁2
0
Wall
L
x
2–51 A spherical metal ball of radius r
o
is heated in an oven
to a temperature of T
i
throughout and is then taken out of the
oven and dropped into a large body of water at T
where it is
cooled by convection with an average convection heat transfer
coefficient of h. Assuming constant thermal conductivity
and transient one-dimensional heat transfer, express the math-
ematical formulation (the differential equation and the bound-
ary and initial conditions) of this heat conduction problem.
Do not solve.
2–52 A spherical metal ball of radius r
o
is heated in an oven
to a temperature of T
i
throughout and is then taken out of the
oven and allowed to cool in ambient air at T
by convection
and radiation. The emissivity of the outer surface of the cylin-
der is e, and the temperature of the surrounding surfaces is
T
surr
. The average convection heat transfer coefficient is esti-
mated to be h. Assuming variable thermal conductivity and
transient one-dimensional heat transfer, express the mathe-
matical formulation (the differential equation and the bound-
ary and initial conditions) of this heat conduction problem.
Do not solve.
cengel_ch02.qxd 1/5/10 10:48 AM Page 119

2–53 Water flows through a pipe at an average temperature
of T
90°C. The inner and outer radii of the pipe are r
1
6 cm and r
2
6.5 cm, respectively. The outer surface of the
pipe is wrapped with a thin electric heater that consumes
400 W per m length of the pipe. The exposed surface of the
heater is heavily insulated so that the entire heat generated in
the heater is transferred to the pipe. Heat is transferred from the
inner surface of the pipe to the water by convection with a heat
transfer coefficient of h 85 W/m
2
·K. Assuming constant
thermal conductivity and one-dimensional heat transfer, ex-
press the mathematical formulation (the differential equation
and the boundary conditions) of the heat conduction in the pipe
during steady operation. Do not solve.
120
HEAT CONDUCTION EQUATION
rod will not vary during steady heat conduction. Do you agree
with this claim? Why?
2–55C It is stated that the temperature in a plane wall with
constant thermal conductivity and no heat generation varies
linearly during steady one-dimensional heat conduction. Will
this still be the case when the wall loses heat by radiation from
its surfaces?
2–56C Consider a solid cylindrical rod whose ends are main-
tained at constant but different temperatures while the side sur-
face is perfectly insulated. There is no heat generation. It is
claimed that the temperature along the axis of the rod varies
linearly during steady heat conduction. Do you agree with this
claim? Why?
2–57C Consider one-dimensional heat conduction through
a large plane wall with no heat generation that is perfectly
insulated on one side and is subjected to convection and radia-
tion on the other side. It is claimed that under steady condi-
tions, the temperature in a plane wall must be uniform (the
same everywhere). Do you agree with this claim? Why?
2–58 Electrically heated draw batch furnaces are commonly
used in the heat treatment industry. Consider a draw batch
furnace front made of a 20-mm thick steel plate with a ther-
mal conductivity of 25 W/m·K. The furnace is situated in a
room with surrounding air temperature of 20 °C and an aver-
age convection heat transfer coefficient of 10 W/m
2
·K. If the
inside surface of the furnace front is subjected to uniform
heat flux of 5 kW/m
2
and the outer surface has an emissivity
of 0.30, determine the inside surface temperature of the fur-
nace front.
Answer:
598 K
FIGURE P2–52
T
i
Metal
ball
Convection
Radiation
r
o
r
0
T
surr
T
⬁
h
Electric heater
Insulation
Water
0
r
1
h
T
⬁
r
2
r
FIGURE P2–53
Solution of Steady One-Dimensional
Heat Conduction Problems
2–54C Consider a solid cylindrical rod whose side surface is
maintained at a constant temperature while the end surfaces
are perfectly insulated. The thermal conductivity of the rod
material is constant and there is no heat generation. It is
claimed that the temperature in the radial direction within the
FIGURE P2–58
0
L
Furnace
front
Air, 20°C
h = 10 W/m
2
⋅K
e = 0.30
k = 25 W/m⋅K
x
T
0
q
0
= 5 kW/m
2
·
T
L
T
surr
= 20°C
2–59 Consider a large plane wall of thickness L 0.3 m,
thermal conductivity k 2.5 W/m·K, and surface area A
12 m
2
. The left side of the wall at x 0 is subjected to a net heat
flux of
q
·
0
700 W/m
2
while the temperature at that surface is
cengel_ch02.qxd 1/5/10 10:48 AM Page 120

CHAPTER 2
121
measured to be T
1
80°C. Assuming constant thermal
conductivity and no heat generation in the wall, (a) express the
differential equation and the boundary conditions for steady one-
dimensional heat conduction through the wall, (b) obtain a rela-
tion for the variation of temperature in the wall by solving the
differential equation, and (c) evaluate the temperature of the
right surface of the wall at x L.
Answer: (c)
4°C
0
L
x
T
1
q
0
·
FIGURE P2–59
0
Base
plate
L
x
112°C
FIGURE P2–64
2–60 Repeat Prob. 2–59 for a heat flux of 1050 W/m
2
and a
surface temperature of 90°C at the left surface at x 0.
2–61 Consider a large plane wall of thickness L 0.4 m,
thermal conductivity k 1.8 W/m·K, and surface area A
30 m
2
. The left side of the wall is maintained at a constant tem-
perature of T
1
90°C while the right side loses heat by con-
vection to the surrounding air at T
25°C with a heat transfer
coefficient of h 24 W/m
2
·K. Assuming constant thermal con-
ductivity and no heat generation in the wall, (a) express the dif-
ferential equation and the boundary conditions for steady
one-dimensional heat conduction through the wall, (b) obtain a
relation for the variation of temperature in the wall by solving
the differential equation, and (c) evaluate the rate of heat trans-
fer through the wall.
Answer: (c)
7079 W
2–62 Consider a solid cylindrical rod of length 0.15 m and
diameter 0.05 m. The top and bottom surfaces of the rod are
maintained at constant temperatures of 20°C and 95°C, respec-
tively, while the side surface is perfectly insulated. Determine
the rate of heat transfer through the rod if it is made of (a) cop-
per, k 380 W/m·K, (b) steel, k 18 W/m·K, and (c) granite,
k 1.2 W/m·K.
2–63 Reconsider Prob. 2–62. Using EES (or other) soft-
ware, plot the rate of heat transfer as a function of
the thermal conductivity of the rod in the range of 1 W/m·K to
400 W/m·K. Discuss the results.
2–64 Consider the base plate of an 800-W household iron
with a thickness of L 0.6 cm, base area of A 160 cm
2
, and
thermal conductivity of k 60 W/m·K. The inner surface
of the base plate is subjected to uniform heat flux generated
by the resistance heaters inside. When steady operating condi-
tions are reached, the outer surface temperature of the plate is
measured to be 112°C. Disregarding any heat loss through the
upper part of the iron, (a) express the differential equation and
the boundary conditions for steady one-dimensional heat con-
duction through the plate, (b) obtain a relation for the variation
of temperature in the base plate by solving the differential
equation, and (c) evaluate the inner surface temperature.
Answer: (c)
127°C
2–65 Repeat Prob. 2–64 for a 1200-W iron.
2–66 Reconsider Prob. 2–64. Using the relation ob-
tained for the variation of temperature in the base
plate, plot the temperature as a function of the distance x in the
range of x 0 to x L, and discuss the results. Use the EES
(or other) software.
2–67 Consider a chilled-water pipe of length L, inner radius
r
1
, outer radius r
2
, and thermal conductivity k. Water flows in
the pipe at a temperature T
f
and the heat transfer coefficient at
the inner surface is h. If the pipe is well-insulated on the outer
surface, (a) express the differential equation and the boundary
conditions for steady one-dimensional heat conduction through
the pipe and (b) obtain a relation for the variation of tempera-
ture in the pipe by solving the differential equation.
2–68 A pipe in a manufacturing plant is transporting super-
heated vapor at a mass flow rate of 0.3 kg/s. The pipe is 10 m
long, has an inner diameter of 5 cm and pipe wall thickness of
6 mm. The pipe has a thermal conductivity of 17 W/m·K, and
the inner pipe surface is at a uniform temperature of 120 °C.
FIGURE P2–68
Superheated
vapor
0.3 kg/s
Air, 25°C
T(r
1
) = 120°C
L = 10 m
T
in
– T
out
= 7°C
r
2
r
1
cengel_ch02.qxd 1/5/10 10:48 AM Page 121

The temperature drop between the inlet and exit of the pipe
is 7 °C, and the constant pressure specific heat of vapor is
2190 J/kg·°C. If the air temperature in the manufacturing plant
is 25 °C, determine the heat transfer coefficient as a result
of convection between the outer pipe surface and the sur-
rounding air.
2-69 In subsea oil and natural gas production, hydrocarbon
fluids may leave the reservoir with a temperature of 70 °C and
flow in subsea surrounding of 5 °C. As a result of the tempera-
ture difference between the reservoir and the subsea surround-
ing, the knowledge of heat transfer is critical to prevent gas
hydrate and wax deposition blockages. Consider a subsea
pipeline with inner diameter of 0.5 m and wall thickness of
8 mm is used for transporting liquid hydrocarbon at an average
temperature of 70 °C, and the average convection heat transfer
coefficient on the inner pipeline surface is estimated to be
250 W/m
2
·K. The subsea surrounding has a temperature of
5 °C and the average convection heat transfer coefficient on the
outer pipeline surface is estimated to be 150 W/m
2
·K. If the
pipeline is made of material with thermal conductivity of
60 W/m·K, by using the heat conduction equation (a) obtain
the temperature variation in the pipeline wall, (b) determine the
inner surface temperature of the pipeline, (c) obtain the mathe-
matical expression for the rate of heat loss from the liquid hy-
drocarbon in the pipeline, and (d) determine the heat flux
through the outer pipeline surface.
122
HEAT CONDUCTION EQUATION
2–71 A spherical container of inner radius r
1
2 m, outer ra-
dius r
2
2.1 m, and thermal conductivity k 30 W/m·K is
filled with iced water at 0°C. The container is gaining heat by
convection from the surrounding air at T
25°C with a heat
transfer coefficient of h 18 W/m
2
·K. Assuming the inner sur-
face temperature of the container to be 0°C, (a) express the dif-
ferential equation and the boundary conditions for steady
one-dimensional heat conduction through the container, (b) ob-
tain a relation for the variation of temperature in the container
by solving the differential equation, and (c) evaluate the rate of
heat gain to the iced water.
2–72E A large steel plate having a thickness of L 4 in,
thermal conductivity of k 7.2 Btu/h·ft·°F, and an emissivity
of e 0.7 is lying on the ground. The exposed surface of the
plate at x L is known to exchange heat by convection with
the ambient air at T
90°F with an average heat transfer co-
efficient of h 12 Btu/h·ft
2
·°F as well as by radiation with the
open sky with an equivalent sky temperature of T
sky
480 R.
Also, the temperature of the upper surface of the plate is mea-
sured to be 80°F. Assuming steady one-dimensional heat trans-
fer, (a) express the differential equation and the boundary
conditions for heat conduction through the plate, (b) obtain a
relation for the variation of temperature in the plate by solving
the differential equation, and (c) determine the value of the
lower surface temperature of the plate at x 0.
FIGURE P2-69
Liquid
hydrocarbon
70°C
S
ubsea, 5°C
h
1
= 250 W/m
2.
Κ
h
2
= 150 W/m
2.
Κ
k = 60 W/m
.
Κ
r
2
r
1
FIGURE P2–70E
L
0
h
r
1
r
2
r
Steam
300°F
T
2
= 175°F
FIGURE P2–72E
L
x
0
Ground
80°F
Radiation
T
sky
Plate
h, T
⬁
Convection
ε
2–70E Consider a steam pipe of length L 30 ft, inner ra-
dius r
1
2 in, outer radius r
2
2.4 in, and thermal conduc-
tivity k 7.2 Btu/h·ft·°F. Steam is flowing through the pipe at
an average temperature of 300°F, and the average convection
heat transfer coefficient on the inner surface is given to be h
1.25 Btu/h·ft
2
·°F. If the average temperature on the outer sur-
faces of the pipe is T
2
175°F, (a) express the differential equa-
tion and the boundary conditions for steady one-dimensional
heat conduction through the pipe, (b) obtain a relation for the
variation of temperature in the pipe by solving the differential
equation, and (c) evaluate the rate of heat loss from the steam
through the pipe.
Answer: (c)
46,660 Btu/h
cengel_ch02.qxd 1/5/10 10:48 AM Page 122

CHAPTER 2
123
2–73E Repeat Prob. 2–72E by disregarding radiation heat
transfer.
2–74 In a food processing facility, a spherical container of
inner radius r
1
⫽ 40 cm, outer radius r
2
⫽ 41 cm, and thermal
conductivity k ⫽ 1.5 W/m·K is used to store hot water and to
keep it at 100°C at all times. To accomplish this, the outer sur-
face of the container is wrapped with a 800-W electric strip
heater and then insulated. The temperature of the inner surface
of the container is observed to be nearly 120°C at all times.
Assuming 10 percent of the heat generated in the heater is lost
through the insulation, (a) express the differential equation
and the boundary conditions for steady one-dimensional heat
conduction through the container, (b) obtain a relation for the
variation of temperature in the container material by solving
the differential equation, and (c) evaluate the outer surface
temperature of the container. Also determine how much water
at 100°C this tank can supply steadily if the cold water enters
at 20°C.
2–79C Consider the uniform heating of a plate in an environ-
ment at a constant temperature. Is it possible for part of the heat
generated in the left half of the plate to leave the plate through
the right surface? Explain.
2–80C Does heat generation in a solid violate the first law of
thermodynamics, which states that energy cannot be created or
destroyed? Explain.
2–81 Consider a large 5-cm-thick brass plate (k ⫽
111 W/m·K) in which heat is generated uniformly at a rate of
2 ⫻ 10
5
W/m
3
. One side of the plate is insulated while the
other side is exposed to an environment at 25°C with a heat
transfer coefficient of 44 W/m
2
·K. Explain where in the plate
the highest and the lowest temperatures will occur, and deter-
mine their values.
2–75 Reconsider Prob. 2–74. Using the relation ob-
tained for the variation of temperature in the con-
tainer material, plot the temperature as a function of the radius r
in the range of r ⫽ r
1
to r ⫽ r
2
, and discuss the results. Use the
EES (or other) software.
Heat Generation in a Solid
2–76C Consider uniform heat generation in a cylinder and a
sphere of equal radius made of the same material in the same
environment. Which geometry will have a higher temperature
at its center? Why?
2–77C What is heat generation? Give some examples.
2–78C An iron is left unattended and its base temperature
rises as a result of resistance heating inside. When will the rate
of heat generation inside the iron be equal to the rate of heat
loss from the iron?
FIGURE P2–74
r
Insulation
Electric
heater
Spherical
container
0
120°C
Hot
water
r
1
r
2
FIGURE P2–81
h
T
⬁
Brass
plate
L
x
e
gen
·
0
Insulated
2–82 Reconsider Prob. 2–81. Using EES (or other) soft-
ware, investigate the effect of the heat transfer co-
efficient on the highest and lowest temperatures in the plate.
Let the heat transfer coefficient vary from 20 W/m
2
·K to 100
W/m
2
·K. Plot the highest and lowest temperatures as a function
of the heat transfer coefficient, and discuss the results.
2–83 A cylindrical nuclear fuel rod of 1 cm in diameter is en-
cased in a concentric tube of 2 cm in diameter, where cooling
water flows through the annular region between the fuel rod
(k ⫽ 30 W/m·K) and the concentric tube. Heat is generated
uniformly in the rod at a rate of 50 MW/m
3
. The convection
heat transfer coefficient for the concentric tube surface is
FIGURE P2–83
Cooling water
Fuel rod
k = 30 W/m
.
Κ
h
1
, T
s,rod
D
2
= 2r
2
= 2 cm
D
1
= 2r
1
= 1 cm
h
2
= 2000 W/m
2
.
Κ
T
s,tube
= 40°C
e
gen
= 50 MW/m
3
·
cengel_ch02.qxd 1/7/10 4:50 PM Page 123

2000 W/m
2
·K. If the surface temperature of the concentric tube
is 40 °C, determine the average temperature of the cooling wa-
ter. Can one use the given information to determine the surface
temperature of the fuel rod? Explain.
Answer:
71.3°C
2–84 A spherical communication satellite with a diameter of
2.5 m is orbiting around the earth. The outer surface of the
satellite in space has an emissivity of 0.75 and a solar absorp-
tivity of 0.10, while solar radiation is incident on the spacecraft
at a rate of 1000 W/m
2
. If the satellite is made of material with
an average thermal conductivity of 5 W/m·K and the midpoint
temperature is 0 °C, determine the heat generation rate and the
surface temperature of the satellite.
124
HEAT CONDUCTION EQUATION
T
s
80°C. The variation of temperature in the cylinder is
given by
T(r) 1 T
s
Based on this relation, determine (a) if the heat conduction is
steady or transient, (b) if it is one-, two-, or three-dimensional,
and (c) the value of heat flux on the side surface of the cylinder
at r r
o
.
2–87 Reconsider Prob. 2–86. Using the relation ob-
tained for the variation of temperature in the
cylinder, plot the temperature as a function of the radius r in
the range of r 0 to r r
o
, and discuss the results. Use the
EES (or other) software.
2–88 Consider a large plate of thickness L and thermal con-
ductivity k in which heat is generated uniformly at a rate
of
e
·
gen
. One side of the plate is insulated while the other side is
exposed to an environment at T
with a heat transfer coefficient
of h. (a) Express the differential equation and the boundary
conditions for steady one-dimensional heat conduction through
the plate, (b) determine the variation of temperature in the
plate, and (c) obtain relations for the temperatures on both sur-
faces and the maximum temperature rise in the plate in terms
of given parameters.
a
r
r
o
b
2
d
冤
e
.
gen
r
2
o
k
2–85 A 2-kW resistance heater wire with thermal conductiv-
ity of k 20 W/m·K, a diameter of D 4 mm, and a length of
L 0.9 m is used to boil water. If the outer surface temperature
of the resistance wire is T
s
230°C, determine the temperature
at the center of the wire.
FIGURE P2–84
q
rad
·
e = 0.75
q
abs
·
a
s
= 0.10
T
s
Satellite
k = 5 W/m
.
K
T
0
= 0°C
e
gen
·
FIGURE P2–85
230°C
0
Resistance
heater
D
r
0
r
r
o
Resistance
heater
Water
T
⬁
h
FIGURE P2–89
FIGURE P2–88
T
⬁
h
0
L
x
k
e
gen
·
Insulated
2–86 Consider a long solid cylinder of radius r
o
4 cm and
thermal conductivity k 25 W/m·K. Heat is generated in the
cylinder uniformly at a rate of
e
·
gen
35 W/cm
3
. The side sur-
face of the cylinder is maintained at a constant temperature of
2–89 A long homogeneous resistance wire of radius r
o
0.6 cm and thermal conductivity k 15.2 W/m·K is being
used to boil water at atmospheric pressure by the passage of
electric current. Heat is generated in the wire uniformly as a
result of resistance heating at a rate of 16.4 W/cm
3
. The heat
generated is transferred to water at 100°C by convection with
cengel_ch02.qxd 1/5/10 10:48 AM Page 124

CHAPTER 2
125
an average heat transfer coefficient of h 3200 W/m
2
·K. As-
suming steady one-dimensional heat transfer, (a) express the
differential equation and the boundary conditions for heat
conduction through the wire, (b) obtain a relation for the vari-
ation of temperature in the wire by solving the differential
equation, and (c) determine the temperature at the centerline
of the wire.
Answer: (c)
125°C
2–90 Reconsider Prob. 2–89. Using the relation ob-
tained for the variation of temperature in the
wire, plot the temperature at the centerline of the wire as a
function of the heat generation
e
·
gen
in the range of 10 W/cm
3
to 100 w/cm
3
, and discuss the results. Use the EES (or other)
software.
2–91 In a nuclear reactor, 1-cm-diameter cylindrical uranium
rods cooled by water from outside serve as the fuel. Heat is
generated uniformly in the rods (k 29.5 W/m·K) at a rate of
4 10
7
W/m
3
. If the outer surface temperature of rods is
220°C, determine the temperature at their center.
the thermal conductivity of the sphere is k 15 W/m·K.
Assuming steady one-dimensional heat transfer, (a) express
the differential equation and the boundary conditions for heat
conduction through the sphere, (b) obtain a relation for the
variation of temperature in the sphere by solving the differen-
tial equation, and (c) determine the temperature at the center
of the sphere.
FIGURE P2–91
Uranium rod
220°C
e
gen
·
2–92 Consider a large 3-cm-thick stainless steel plate (k
15.1 W/m·K) in which heat is generated uniformly at a rate of
5 10
5
W/m
3
. Both sides of the plate are exposed to an envi-
ronment at 30°C with a heat transfer coefficient of 60 W/m
2
·K.
Explain where in the plate the highest and the lowest tempera-
tures will occur, and determine their values.
2–93 A 6-m-long 3-kW electrical resistance wire is made of
0.2-cm-diameter stainless steel (k 15.1 W/m·K). The resis-
tance wire operates in an environment at 20°C with a heat
transfer coefficient of 175 W/m
2
·K at the outer surface. Deter-
mine the surface temperature of the wire (a) by using the ap-
plicable relation and (b) by setting up the proper differential
equation and solving it.
Answers: (a)
475°C,
(b)
475°C
2–94E Heat is generated uniformly at a rate of 3 kW per ft
length in a 0.08-in-diameter electric resistance wire made of
nickel steel (k 5.8 Btu/h·ft·°F). Determine the temperature
difference between the centerline and the surface of the wire.
2–95E Repeat Prob. 2–94E for a manganese wire (k
4.5 Btu/h·ft·°F).
2–96 Consider a homogeneous spherical piece of radioactive
material of radius r
o
0.04 m that is generating heat at a con-
stant rate of
e
·
gen
5 10
7
W/m
3
. The heat generated is dis-
sipated to the environment steadily. The outer surface of the
sphere is maintained at a uniform temperature of 110°C and
2–97 Reconsider Prob. 2–96. Using the relation ob-
tained for the variation of temperature in the
sphere, plot the temperature as a function of the radius r in the
range of r 0 to r r
o
. Also, plot the center temperature of
the sphere as a function of the thermal conductivity in the
range of 10 W/m·K to 400 W/m·K. Discuss the results. Use the
EES (or other) software.
2–98 A long homogeneous resistance wire of radius r
o
5 mm is being used to heat the air in a room by the passage of
electric current. Heat is generated in the wire uniformly at a
rate of 5 10
7
W/m
3
as a result of resistance heating. If the
temperature of the outer surface of the wire remains at 180°C,
determine the temperature at r 3.5 mm after steady operation
conditions are reached. Take the thermal conductivity of the
wire to be k 6 W/m·K.
Answer:
207°C
FIGURE P2–96
0
110°C
r
o
r
e
gen
.
FIGURE P2–98
0
r
r
o
180°C
e
gen
·
2–99 Consider a large plane wall of thickness L 0.05 m.
The wall surface at x 0 is insulated, while the surface at x
L is maintained at a temperature of 30°C. The thermal conduc-
tivity of the wall is k 30 W/m·K, and heat is generated in the
wall at a rate of
e
·
gen
e
·
0
e
0.5x/L
W/m
3
where e
·
0
8 10
6
W/m
3
. Assuming steady one-dimensional heat transfer, (a) ex-
press the differential equation and the boundary conditions for
heat conduction through the wall, (b) obtain a relation for the
cengel_ch02.qxd 1/5/10 10:48 AM Page 125

variation of temperature in the wall by solving the differential
equation, and (c) determine the temperature of the insulated
surface of the wall.
Answer: (c)
314°C
2–100 Reconsider Prob. 2–99. Using the relation given
for the heat generation in the wall, plot the heat
generation as a function of the distance x in the range of
x 0 to x L, and discuss the results. Use the EES (or other)
software.
Variable Thermal Conductivity,
k
(
T
)
2–101C The temperature of a plane wall during steady one-
dimensional heat conduction varies linearly when the thermal
conductivity is constant. Is this still the case when the thermal
conductivity varies linearly with temperature?
2–102C Is the thermal conductivity of a medium, in general,
constant or does it vary with temperature?
2–103C Consider steady one-dimensional heat conduction in
a plane wall in which the thermal conductivity varies linearly.
The error involved in heat transfer calculations by assuming
constant thermal conductivity at the average temperature is
(a) none, (b) small, or (c) significant.
2–104C Consider steady one-dimensional heat conduction in
a plane wall, long cylinder, and sphere with constant thermal
conductivity and no heat generation. Will the temperature in
any of these mediums vary linearly? Explain.
2–105C When the thermal conductivity of a medium varies
linearly with temperature, is the average thermal conductivity
always equivalent to the conductivity value at the average
temperature?
2–106 A silicon wafer with thickness of 925 mm is being
heated with a uniform heat flux at the lower surface. The sili-
con wafer has a thermal conductivity that varies with tempera-
ture and can be expressed as k(T) (a + bT + cT
2
) W/m·K,
where a 437, b –1.29, and c 0.00111. To avoid warp-
ing, the temperature difference across the wafer thickness can-
not exceed 2 °C. If the upper surface of the silicon wafer is at a
uniform temperature of 600 K, determine the maximum allow-
able heat flux.
Answer:
1.35 10
5
W/m
2
126
HEAT CONDUCTION EQUATION
2–107 Consider a plane wall of thickness L whose thermal
conductivity varies in a specified temperature range as k(T )
k
0
(1 bT
2
) where k
0
and b are two specified constants. The
wall surface at x 0 is maintained at a constant temperature of
T
1
, while the surface at x L is maintained at T
2
. Assuming
steady one-dimensional heat transfer, obtain a relation for the
heat transfer rate through the wall.
2–108 Consider a cylindrical shell of length L, inner radius
r
1
, and outer radius r
2
whose thermal conductivity varies lin-
early in a specified temperature range as k(T) k
0
(1 bT)
where k
0
and b are two specified constants. The inner surface
of the shell is maintained at a constant temperature of T
1
, while
the outer surface is maintained at T
2
. Assuming steady one-
dimensional heat transfer, obtain a relation for (a) the heat
transfer rate through the wall and (b) the temperature distribu-
tion T(r) in the shell.
2–109 Consider a spherical shell of inner radius r
1
and outer ra-
dius r
2
whose thermal conductivity varies linearly in a specified
temperature range as k(T) k
0
(1 bT) where k
0
and b are two
specified constants. The inner surface of the shell is maintained
at a constant temperature of T
1
while the outer surface is main-
tained at T
2
. Assuming steady one-dimensional heat transfer,
obtain a relation for (a) the heat transfer rate through the shell
and (b) the temperature distribution T(r) in the shell.
2–110 Consider a 1.5-m-high and 0.6-m-wide plate whose
thickness is 0.15 m. One side of the plate is maintained at a
constant temperature of 500 K while the other side is main-
tained at 350 K. The thermal conductivity of the plate can be
assumed to vary linearly in that temperature range as k(T)
k
0
(1 bT) where k
0
18 W/m·K and b 8.7 10
4
K
1
.
Disregarding the edge effects and assuming steady one-dimen-
sional heat transfer, determine the rate of heat conduction
through the plate.
Answer:
22.2 kW
2–111 Reconsider Prob. 2–110. Using EES (or other)
software, plot the rate of heat conduction through
the plate as a function of the temperature of the hot side of the
plate in the range of 400 K to 700 K. Discuss the results.
FIGURE P2-106
L
x
0
T
2
T
1
q
.
Silicon wafer
k(T) = a + bT + cT
2
FIGURE P2–108
h
0
r
1
r
2
r
Cylindrical
shell
T
2
k(T)
T
1
cengel_ch02.qxd 1/5/10 10:48 AM Page 126

CHAPTER 2
127
Special Topic: Review of Differential Equations
2–112C Why do we often utilize simplifying assumptions
when we derive differential equations?
2–113C What is a variable? How do you distinguish a de-
pendent variable from an independent one in a problem?
2–114C Can a differential equation involve more than one in-
dependent variable? Can it involve more than one dependent
variable? Give examples.
2–115C What is the geometrical interpretation of a deriva-
tive? What is the difference between partial derivatives and
ordinary derivatives?
2–116C What is the difference between the degree and the
order of a derivative?
2–117C Consider a function f(x, y) and its partial derivative
f/x. Under what conditions will this partial derivative be
equal to the ordinary derivative df/dx?
2–118C Consider a function f(x) and its derivative df/dx.
Does this derivative have to be a function of x?
2–119C How is integration related to derivation?
2–120C What is the difference between an algebraic equa-
tion and a differential equation?
2–121C What is the difference between an ordinary differen-
tial equation and a partial differential equation?
2–122C How is the order of a differential equation determined?
2–123C How do you distinguish a linear differential equation
from a nonlinear one?
2–124C How do you recognize a linear homogeneous differ-
ential equation? Give an example and explain why it is linear
and homogeneous.
2–125C How do differential equations with constant coeffi-
cients differ from those with variable coefficients? Give an ex-
ample for each type.
2–126C What kind of differential equations can be solved by
direct integration?
2–127C Consider a third order linear and homogeneous dif-
ferential equation. How many arbitrary constants will its gen-
eral solution involve?
Review Problems
2–128 In a manufacturing plant, a quench hardening process
is used to treat steel ball bearings (c 500 J/kg·K, k
60 W/m·K, r 7900 kg/m
3
) of 25 mm in diameter. After being
heated to a prescribed temperature, the steel ball bearings are
quenched. Determine the rate of heat loss if the rate of temper-
ature decrease at the ball bearing surface at a given instant dur-
ing the quenching process is 50 K/s.
Answer:
12.9 kW
2–129 Consider a spherical reactor of 5-cm diameter operat-
ing at steady condition has a temperature variation that can be
expressed in the form of T(r) a – br
2
, where a 850 °C and
b 5 10
5
K/m
2
. The reactor is made of material with c
200 J/kg·°C, k 40 W/m·K, r 9000 kg/m
3
. If the heat gen-
eration of reactor is suddenly set to 9 MW/m
3
, determine the
time rate of temperature change in the reactor. Is the heat gen-
eration of reactor suddenly increased or decreased to 9 MW/m
3
from its steady operating condition?
2–130 Consider a small hot metal object of mass m and spe-
cific heat c that is initially at a temperature of T
i
. Now the object
is allowed to cool in an environment at T
by convection with a
heat transfer coefficient of h. The temperature of the metal ob-
ject is observed to vary uniformly with time during cooling.
Writing an energy balance on the entire metal object, derive the
differential equation that describes the variation of temperature
of the ball with time, T(t). Assume constant thermal conductiv-
ity and no heat generation in the object. Do not solve.
h
T
⬁
A
T = T(t)
m, c, T
i
FIGURE P2–130
2–131 Consider a long rectangular bar of length a in the x-
direction and width b in the y-direction that is initially at a uni-
form temperature of T
i
. The surfaces of the bar at x 0 and
y 0 are insulated, while heat is lost from the other two sur-
faces by convection to the surrounding medium at temperature
T
with a heat transfer coefficient of h. Assuming constant ther-
mal conductivity and transient two-dimensional heat transfer
with no heat generation, express the mathematical formulation
(the differential equation and the boundary and initial condi-
tions) of this heat conduction problem. Do not solve.
FIGURE P2–131
y
x
h
a
b
hT
i
T
⬁
0
2–132 Consider a short cylinder of radius r
o
and height H in
which heat is generated at a constant rate of
e
·
gen
. Heat is lost
from the cylindrical surface at r r
o
by convection to the
surrounding medium at temperature T
with a heat transfer
cengel_ch02.qxd 1/5/10 10:48 AM Page 127

coefficient of h. The bottom surface of the cylinder at z 0 is
insulated, while the top surface at z H is subjected to uni-
form heat flux
q
·
H
. Assuming constant thermal conductivity
and steady two-dimensional heat transfer, express the mathe-
matical formulation (the differential equation and the bound-
ary conditions) of this heat conduction problem. Do not solve.
2–133E The roof of a house consists of a 0.8-ft-thick con-
crete slab (k 1.1 Btu/h·ft·°F) that is 25 ft wide and 35 ft long.
The emissivity of the outer surface of the roof is 0.8, and the
convection heat transfer coefficient on that surface is estimated
to be 3.2 Btu/h·ft
2
·°F. On a clear winter night, the ambient air is
reported to be at 50°F, while the night sky temperature for ra-
diation heat transfer is 310 R. If the inner surface temperature
of the roof is T
1
62°F, determine the outer surface tempera-
ture of the roof and the rate of heat loss through the roof when
steady operating conditions are reached.
128
HEAT CONDUCTION EQUATION
temperature of T
0
with a heat transfer coefficient of h
o
. Assum-
ing steady one-dimensional heat conduction through the pipe,
(a) express the differential equation and the boundary condi-
tions for heat conduction through the pipe material, (b) obtain
a relation for the variation of temperature in the pipe material
by solving the differential equation, and (c) obtain a relation
for the temperature of the outer surface of the pipe.
2–135 The boiling temperature of nitrogen at atmospheric
pressure at sea level (1 atm pressure) is 196°C. Therefore, ni-
trogen is commonly used in low temperature scientific studies
since the temperature of liquid nitrogen in a tank open to the at-
mosphere remains constant at 196°C until the liquid nitrogen
in the tank is depleted. Any heat transfer to the tank results in
the evaporation of some liquid nitrogen, which has a heat of va-
porization of 198 kJ/kg and a density of 810 kg/m
3
at 1 atm.
Consider a thick-walled spherical tank of inner radius r
1
2 m, outer radius r
2
2.1 m, and constant thermal conductiv-
ity k 12 W/m·K. The tank is initially filled with liquid nitro-
gen at 1 atm and 196°C, and is exposed to ambient air at
T
20°C with a heat transfer coefficient of h 35 W/m
2
·K.
The inner surface temperature of the spherical tank is observed
to be almost the same as the temperature of the nitrogen inside.
Assuming steady one-dimensional heat transfer, (a) express the
differential equation and the boundary conditions for heat con-
duction through the tank, (b) obtain a relation for the variation
of temperature in the tank material by solving the differential
equation, and (c) determine the rate of evaporation of the liquid
nitrogen in the tank as a result of the heat transfer from the am-
bient air.
Answer: (c)
1.62 kg/s
2–136 Repeat Prob. 2–135 for liquid oxygen, which has a
boiling temperature of 183°C, a heat of vaporization of 213
kJ/kg, and a density of 1140 kg/m
3
at 1 atm.
2–137 Consider a large plane wall of thickness L 0.4 m and
thermal conductivity k 8.4 W/m·K. There is no access to the
inner side of the wall at x 0 and thus the thermal conditions on
that surface are not known. However, the outer surface of the
wall at x L, whose emissivity is e 0.7, is known to exchange
heat by convection with ambient air at T
25°C with an aver-
age heat transfer coefficient of h 14 W/m
2
·K as well as by
FIGURE P2–133E
T
sky
T
⬁
h
T
1
0
L
y
Concrete
FIGURE P2–134
L
h
0
r
1
r
2
r
h
i
T
i
h
o
T
0
FIGURE P2–137
T
surr
h
T
⬁
0
Plane
wall
45°C
L
x
2–134 Consider a steam pipe of length L, inner radius r
1
,
outer radius r
2
, and constant thermal conductivity k. Steam
flows inside the pipe at an average temperature of T
i
with a
convection heat transfer coefficient of h
i
. The outer surface of
the pipe is exposed to convection to the surrounding air at a
cengel_ch02.qxd 1/5/10 10:48 AM Page 128

CHAPTER 2
129
radiation with the surrounding surfaces at an average tempera-
ture of T
surr
290 K. Further, the temperature of the outer sur-
face is measured to be T
2
45°C. Assuming steady
one-dimensional heat transfer, (a) express the differential equa-
tion and the boundary conditions for heat conduction through the
plate, (b) obtain a relation for the temperature of the outer sur-
face of the plate by solving the differential equation, and (c) eval-
uate the inner surface temperature of the wall at x 0.
Answer:
(c)
64.3°C
2–138 A 1200-W iron is left on the iron board with its base
exposed to ambient air at 26°C. The base plate of the iron has
a thickness of L 0.5 cm, base area of A 150 cm
2
, and ther-
mal conductivity of k 18 W/m·K. The inner surface of the
base plate is subjected to uniform heat flux generated by the
resistance heaters inside. The outer surface of the base plate
whose emissivity is e 0.7, loses heat by convection to ambi-
ent air with an average heat transfer coefficient of h
30 W/m
2
·K as well as by radiation to the surrounding surfaces
at an average temperature of T
surr
295 K. Disregarding any
heat loss through the upper part of the iron, (a) express the dif-
ferential equation and the boundary conditions for steady one-
dimensional heat conduction through the plate, (b) obtain a
relation for the temperature of the outer surface of the plate by
solving the differential equation, and (c) evaluate the outer
surface temperature.
2–141E Repeat Prob. 2–140E for the case of no solar radia-
tion incident on the surface.
2–142 Consider a long resistance wire of radius r
1
0.3 cm
and thermal conductivity k
wire
18 W/m·K in which heat is gen-
erated uniformly at a constant rate of
e
·
gen
4.8 W/cm
3
as
a result of resistance heating. The wire is embedded in a
0.4-cm-thick layer of plastic whose thermal conductivity is k
plastic
1.8 W/m·K. The outer surface of the plastic cover loses heat
by convection to the ambient air at T
25°C with an average
combined heat transfer coefficient of h 14 W/m
2
·K. Assuming
one-dimensional heat transfer, determine the temperatures at the
center of the resistance wire and the wire-plastic layer interface
under steady conditions.
Answers:
255.7°C, 266.3°C
FIGURE P2–138
T
surr
h
T
⬁
0
Iron
base
plate
L
x
FIGURE P2–140E
0
Plate
L
x
520 R
q
solar
·
Sun
2–139 Repeat Prob. 2–138 for a 1500-W iron.
2–140E Consider a large plane wall of thickness L 0.8 ft
and thermal conductivity k 1.2 Btu/h·ft·°F. The wall is cov-
ered with a material that has an emissivity of e 0.80 and a
solar absorptivity of a 0.60. The inner surface of the wall
is maintained at T
1
520 R at all times, while the outer sur-
face is exposed to solar radiation that is incident at a rate of
q
·
solar
300 Btu/h·ft
2
. The outer surface is also losing heat by
radiation to deep space at 0 K. Determine the temperature of
the outer surface of the wall and the rate of heat transfer
through the wall when steady operating conditions are
reached.
Answers:
554 R, 50.9 Btu/h·ft
2
FIGURE P2–142
T
⬁
h
Wire
r
1
r
2
r
Plastic cover
e
gen
·
2–143 Consider a cylindrical shell of length L, inner radius
r
1
, and outer radius r
2
whose thermal conductivity varies in a
specified temperature range as k(T) k
0
(1 bbT
2
) where k
0
and b are two specified constants. The inner surface of the shell
is maintained at a constant temperature of T
1
while the outer
surface is maintained at T
2
. Assuming steady one-dimensional
heat transfer, obtain a relation for the heat transfer rate through
the shell.
cengel_ch02.qxd 1/5/10 10:48 AM Page 129

130
HEAT CONDUCTION EQUATION
2–144 In a nuclear reactor, heat is generated in 1-cm-
diameter cylindrical uranium fuel rods at a rate of 4 10
7
W/m
3
.
Determine the temperature difference between the center and
the surface of the fuel rod.
Answer:
9.0°C
(a) Determine the convection coefficient between the wall
and water.
(b) Show that the steady-state temperature distribution has
the form T(x) ax
2
bx c, and determine the values
and units of a, b, and c. The origin of x is shown in the
figure.
(c) Determine the location and value of the maximum tem-
perature in the wall. Could this location be found with-
out knowing a, b, and c, but knowing that T(x) is a
quadratic function? Explain.
2–148 A plane wall of thickness 2L 50 mm and constant
thermal conductivity k 8 W/m·K experiences uniform heat
generation at a rate
e
·
gen
. Under steady conditions, the temper-
ature distribution in the wall is of the form T(x) abx
2
,
where a 80°C and b 2 10
4
°C/m
2
,and x is in meters.
The origin of the x coordinate is at the midplane of the wall.
(a) Determine the surface temperatures and sketch the tem-
perature distribution in the wall.
(b) What is the volumetric rate of heat generation,
e
·
gen
?
(c) Determine the surface heat fluxes
q
·
s
(L) and q
·
s
(L).
(d) What is the relationship between these fluxes, the heat
generation rate and the geometry of the wall?
2–149 Steady one-dimensional heat conduction takes place
in a long slab of width W (in the direction of heat flow, x) and
thickness Z. The slab’s thermal conductivity varies with tem-
perature as k k*/(T* T), where T is the temperature (in K),
and k* (in W/m) and T* (in K) are two constants. The temper-
atures at x 0 and x W are T
0
and T
W
, respectively. Show
that the heat flux in steady operation is given by
q
·
ln
Also, calculate the heat flux for T* 1000 K, T
0
600 K,
T
W
400 K, k* 7 10
4
W/m, and W 20 cm.
2–150 Heat is generated uniformly at a rate of 4.2 10
6
W/m
3
in a spherical ball (k 45 W/m·K) of diameter 24 cm.
The ball is exposed to iced-water at 0°C with a heat transfer co-
efficient of 1200 W/m
2
·K. Determine the temperatures at the
center and the surface of the ball.
2-151 Exhaust gases from a manufacturing plant are being
discharged through a 10-m tall exhaust stack with outer diam-
eter of 1 m, wall thickness of 10 cm, and thermal conductivity
of 40 W/m·K. The exhaust gases are discharged at a rate of
1.2 kg/s, while temperature drop between inlet and exit of the
exhaust stack is 30 °C, and the constant pressure specific heat
of the exhaust gasses is 1600 J/kg·K. On a particular day, the
outer surface of the exhaust stack experiences radiation with
the surrounding at 27 °C, and convection with the ambient air
at 27 °C also, with an average convection heat transfer coeffi-
cient of 8 W/m
2
·K. Solar radiation is incident on the exhaust
stack outer surface at a rate of 150 W/m
2
, and both the emis-
sivity and solar absorptivity of the outer surface are 0.9.
a
T* T
0
T* T
W
b
k*
W
2–145 Consider a 20-cm-thick large concrete plane wall (k
0.77 W/m·K) subjected to convection on both sides with T
1
22°C and h
1
8 W/m
2
·K on the inside, and T
2
8°C and
h
2
12 W/m
2
·K on the outside. Assuming constant thermal
conductivity with no heat generation and negligible radiation,
(a) express the differential equations and the boundary condi-
tions for steady one-dimensional heat conduction through the
wall, (b) obtain a relation for the variation of temperature in
the wall by solving the differential equation, and (c) evaluate
the temperatures at the inner and outer surfaces of the wall.
2–146 Consider a water pipe of length L 17 m, inner
radius r
1
15 cm, outer radius r
2
20 cm, and thermal con-
ductivity k 14 W/m·K. Heat is generated in the pipe material
uniformly by a 25-kW electric resistance heater. The inner and
outer surfaces of the pipe are at T
1
60°C and T
2
80°C, re-
spectively. Obtain a general relation for temperature distribu-
tion inside the pipe under steady conditions and determine the
temperature at the center plane of the pipe.
2–147 A plane wall of thickness L 4 cm has a thermal con-
ductivity of k 20 W/m·K. A chemical reaction takes place in-
side the wall resulting in a uniform heat generation at a rate of
e
·
gen
10
5
W/m
3
. Sandwiched between the wall and an insulat-
ing layer is a film heater of negligible thickness that generates
a heat flux
q
·
s
16 kW/m
2
. The opposite side of the wall is in
contact with water at temperature T
40°C. A thermocouple
mounted on the surface of the wall in contact with the water
reads T
s
90°C.
FIGURE P2–144
Fuel rod
T
s
e
gen
·
D
FIGURE P2–147
L
k
q
s
T
s
x
Heater
Insulation
T
⬁
, h
e
gen
.
.
cengel_ch02.qxd 1/5/10 10:48 AM Page 130

CHAPTER 2
131
Fundamentals of Engineering (FE) Exam Problems
2–152 The heat conduction equation in a medium is given in
its simplest form as
Select the wrong statement below.
(a) The medium is of cylindrical shape.
(b) The thermal conductivity of the medium is constant.
(c) Heat transfer through the medium is steady.
(d) There is heat generation within the medium.
(e) Heat conduction through the medium is one-dimensional.
2–153 Heat is generated in a long 0.3-cm-diameter cylindri-
cal electric heater at a rate of 180 W/cm
3
. The heat flux at the
surface of the heater in steady operation is
(a) 12.7 W/cm
2
(b) 13.5 W/cm
2
(c) 64.7 W/cm
2
(d) 180 W/cm
2
(e) 191 W/cm
2
2–154 Heat is generated in a 10-cm-diameter spherical ra-
dioactive material whose thermal conductivity is 25 W/m·K
uniformly at a rate of 15 W/cm
3
. If the surface temperature of
the material is measured to be 120°C, the center temperature of
the material during steady operation is
(a) 160°C (b) 205°C (c) 280°C
(d) 370°C (e) 495°C
2–155 Consider a medium in which the heat conduction
equation is given in its simplest forms as
(a) Is heat transfer steady or transient?
(b) Is heat transfer one-, two-, or three-dimensional?
T
t
1
a
ar
2
T
r
b
r
1
r
2
ark
dT
dr
b e
.
gen
0
d
dr
1
r
(c) Is there heat generation in the medium?
(d) Is the thermal conductivity of the medium constant or
variable?
(e) Is the medium a plane wall, a cylinder, or a sphere?
(f) Is this differential equation for heat conduction linear or
nonlinear?
2–156 An apple of radius R is losing heat steadily and uni-
formly from its outer surface to the ambient air at temperature
T
with a convection coefficient of h, and to the surrounding
surfaces at temperature T
surr
(all temperatures are absolute tem-
peratures). Also, heat is generated within the apple uniformly
at a rate of
e
·
gen
per unit volume. If T
s
denotes the outer surface
temperature, the boundary condition at the outer surface of the
apple can be expressed as
(a) k h(T
s
T
) es()
(b) k h(T
s
T
) es() e
·
gen
(c) k h(T
s
T
) es()
(d) k h(T
s
T
) es() e
·
gen
(e) None of them
2–157 A furnace of spherical shape is losing heat steadily
and uniformly from its outer surface of radius R to the ambient
air at temperature T
with a convection coefficient of h, and to
the surrounding surfaces at temperature T
surr
(all temperatures
are absolute temperatures). If T
0
denotes the outer surface tem-
perature, the boundary condition at the outer surface of the fur-
nace can be expressed as
(a) k h(T
0
T
) es()
(b) k h(T
0
T
) es()
(c) k h(T
0
T
) es()
(d) k h(T
0
T
) es()
(e) k(4pR
2
) h(T
0
T
) es()
2–158 A plane wall of thickness L is subjected to convection
at both surfaces with ambient temperature T
1
and heat transfer
coefficient h
1
at inner surface, and corresponding T
2
and h
2
values at the outer surface. Taking the positive direction of x to
be from the inner surface to the outer surface, the correct ex-
pression for the convection boundary condition is
T
0
4
T
4
surr
dT
dr
`
rR
T
0
4
T
4
surr
dT
dr
`
rR
T
0
4
T
4
surr
dT
dr
`
rR
T
0
4
T
4
surr
dT
dr
`
rR
T
0
4
T
4
surr
dT
dr
`
rR
4pR
3
/3
4pR
2
T
s
4
T
4
surr
dT
dr
`
rR
T
s
4
T
4
surr
dT
dr
`
rR
T
s
4
T
4
surr
dT
dr
`
rR
T
s
4
T
4
surr
dT
dr
`
rR
FIGURE P2–151
q
loss
.
q
rad
.
q
abs
.
q
conv
.
r
2
r
1
Exhaust
stack wall
k = 40 W/m
.
K
Manufacturing
plant
L = 10 m
Exhaust
stack
Exhaust
gases
T
in
– T
out
= 30°C
a
s
= e = 0.9
Air, 27°C
h = 8 W/m
2
·K
Assuming steady one-dimensional heat transfer, (a) obtain the
variation of temperature in the exhaust stack wall and (b) de-
termine the inner surface temperature of the exhaust stack.
cengel_ch02.qxd 1/5/10 10:48 AM Page 131

(a) k h
1
[T(0) T
1
)]
(b) k h
2
[T(L) T
2
)]
(c) k h
1
[T
1
T
2
)]
(d) k h
2
[T
1
T
2
)]
(e) None of them
2–159 Consider steady one-dimensional heat conduction
through a plane wall, a cylindrical shell, and a spherical shell of
uniform thickness with constant thermophysical properties and
no thermal energy generation. The geometry in which the
variation of temperature in the direction of heat transfer will be
linear is
(a) plane wall (b) cylindrical shell (c) spherical shell
(d) all of them (e) none of them
2–160 Consider a large plane wall of thickness L, thermal
conductivity k, and surface area A. The left surface of the wall
is exposed to the ambient air at T
with a heat transfer coeffi-
cient of h while the right surface is insulated. The variation of
temperature in the wall for steady one-dimensional heat con-
duction with no heat generation is
(a) T(x) T
(b) T(x) T
(c) T(x) T
(d) T(x) (L x) T
(e) T(x) T
2–161 The variation of temperature in a plane wall is deter-
mined to be T(x) 52x 25 where x is in m and T is in °C. If the
temperature at one surface is 38°C, the thickness of the wall is
(a) 0.10 m (b) 0.20 m (c) 0.25 m
(d) 0.40 m (e) 0.50 m
2–162 The variation of temperature in a plane wall is deter-
mined to be T(x) 11060x where x is in m and T is in °C. If
the thickness of the wall is 0.75 m, the temperature difference
between the inner and outer surfaces of the wall is
(a) 30°C (b) 45°C (c) 60°C (d) 75°C (e) 84°C
2–163 The temperatures at the inner and outer surfaces of a
15-cm-thick plane wall are measured to be 40°C and 28°C, re-
spectively. The expression for steady, one-dimensional varia-
tion of temperature in the wall is
(a) T(x) 28x 40 (b) T(x) 40x 28
(c) T(x) 40x 28 (d) T(x)
80x 40
(e) T(x) 40x 80
a1
xh
k
b
k
h(x 0.5L)
h(L x)
k
dT(L)
dx
dT(0)
dx
dT(L)
dx
dT(0)
dx
132
HEAT CONDUCTION EQUATION
2–164 Heat is generated in a 3-cm-diameter spherical ra-
dioactive material uniformly at a rate of 15 W/cm
3
. Heat is dis-
sipated to the surrounding medium at 25°C with a heat transfer
coefficient of 120 W/m
2
·K. The surface temperature of the ma-
terial in steady operation is
(a) 56°C (b) 84°C (c) 494°C
(d) 650°C (e) 108°C
2–165 Which one of the following is the correct expression
for one-dimensional, steady-state, constant thermal conduc-
tivity heat conduction equation for a cylinder with heat
generation?
(a) e
·
gen
rc
(b)
(c)
(d) 0
(e) 0
2–166 A solar heat flux
q
·
s
is incident on a sidewalk whose
thermal conductivity is k, solar absorptivity is
s
, and convec-
tive heat transfer coefficient is h. Taking the positive x direction
to be towards the sky and disregarding radiation exchange with
the surroundings surfaces, the correct boundary condition for
this sidewalk surface is
(a) k a
s
q
.
s
(b) k h(T T
)
(c) k h(T T
) a
s
q
.
s
(d) h(T T
) a
s
q
.
s
(e) None of them
2–167 Hot water flows through a PVC (k 0.092 W/m·K)
pipe whose inner diameter is 2 cm and outer diameter is
2.5 cm. The temperature of the interior surface of this pipe is
50°C and the temperature of the exterior surface is 20°C. The
rate of heat transfer per unit of pipe length is
(a) 77.7 W/m (b) 89.5 W/m (c) 98.0 W/m
(d) 112 W/m (e) 168 W/m
2–168 The thermal conductivity of a solid depends upon the
solid’s temperature as k aT b where a and b are constants.
The temperature in a planar layer of this solid as it conducts
heat is given by
(a) aT b x C
2
(b) aT b C
1
x
2
C
2
(c) aT
2
bT C
1
x C
2
(d) aT
2
bT C
1
x
2
C
2
(e) None of them
2–169 Harvested grains, like wheat, undergo a volumetric
exothermic reaction while they are being stored. This heat
generation causes these grains to spoil or even start fires if not
controlled properly. Wheat (k 0.5 W/m·K) is stored on the
dT
dx
dT
dx
dT
dx
d
dr
ar
dT
dr
b
e
.
gen
k
ar
dT
dr
b
1
r
d
dr
T
t
1
a
ar
T
r
b
1
r
r
T
t
1
a
e
.
gen
k
ar
T
r
b
1
r
r
T
t
ark
T
r
b
1
r
r
cengel_ch02.qxd 1/5/10 10:48 AM Page 132

CHAPTER 2
133
ground (effectively an adiabatic surface) in 5-m-thick layers.
Air at 22°C contacts the upper surface of this layer of wheat
with h 3 W/m
2
·K. The temperature distribution inside this
layer is given by
where T
s
is the upper surface temperature, T
0
is the lower sur-
face temperature, x is measured upwards from the ground, and
L is the thickness of the layer. When the temperature of the up-
per surface is 24°C, what is the temperature of the wheat next
to the ground?
(a) 42°C (b) 54°C (c) 58°C (d) 63°C (e) 76°C
2–170 The conduction equation boundary condition for an
adiabatic surface with direction n being normal to the surface
is
(a) T 0(b) dT/dn 0(c) d
2
T/dn
2
0
(d) d
3
T/dn
3
0(e) kdT/dn 1
2–171 Heat is generated uniformly in a 4-cm-diameter,
12-cm-long solid bar (k 2.4 W/m·K). The temperatures at the
center and at the surface of the bar are measured to be 210°C
T T
s
T
0
T
s
1 a
x
L
b
2
and 45°C, respectively. The rate of heat generation within the
bar is
(a) 597 W (b) 760 W (c) 826 W
(d) 928 W (e) 1020 W
Design and Essay Problems
2–172 Write an essay on heat generation in nuclear fuel rods.
Obtain information on the ranges of heat generation, the varia-
tion of heat generation with position in the rods, and the ab-
sorption of emitted radiation by the cooling medium.
2–173 Write an interactive computer program to calcu-
late the heat transfer rate and the value of temper-
ature anywhere in the medium for steady one-dimensional heat
conduction in a long cylindrical shell for any combination of
specified temperature, specified heat flux, and convection
boundary conditions. Run the program for five different sets of
specified boundary conditions.
2–174 Write an interactive computer program to calculate the
heat transfer rate and the value of temperature anywhere in the
medium for steady one-dimensional heat conduction in a spher-
ical shell for any combination of specified temperature, speci-
fied heat flux, and convection boundary conditions. Run the
program for five different sets of specified boundary conditions.
cengel_ch02.qxd 1/5/10 10:48 AM Page 133
cengel_ch02.qxd 1/5/10 10:48 AM Page 134
