
Georgia State University Georgia State University
ScholarWorks @ Georgia State University ScholarWorks @ Georgia State University
Middle and Secondary Education Dissertations Department of Middle and Secondary Education
Fall 12-21-2018
The Effects of Mathematical Modeling Instruction on Precalculus The Effects of Mathematical Modeling Instruction on Precalculus
Students' Performance and Attitudes Toward Rational Functions Students' Performance and Attitudes Toward Rational Functions
Solomon A. Betanga
Follow this and additional works at: https://scholarworks.gsu.edu/mse_diss
Recommended Citation Recommended Citation
Betanga, Solomon A., "The Effects of Mathematical Modeling Instruction on Precalculus Students'
Performance and Attitudes Toward Rational Functions." Dissertation, Georgia State University, 2018.
doi: https://doi.org/10.57709/13475861
This Dissertation is brought to you for free and open access by the Department of Middle and Secondary Education
at ScholarWorks @ Georgia State University. It has been accepted for inclusion in Middle and Secondary Education
Dissertations by an authorized administrator of ScholarWorks @ Georgia State University. For more information,
please contact [email protected].
ACCEPTANCE
This dissertation, THE EFFECTS OF MATHEMATICAL MODELING INSTRUCTION ON
PRECALCULUS STUDENTS’ PERFORMANCE AND ATTITUDES TOWARD
RATIONAL FUNCTIONS, by SOLOMON A. BETANGA, was prepared under the direction
of the candidate’s Dissertation Advisory Committee. It is accepted by the committee members
in partial fulfillment of the requirements of the degree, Doctor of Philosophy, in the College of
Education & Human Development, Georgia State University.
The Dissertation Advisory Committee and the student’s Department Chairperson, as
representatives of the faculty, certify that this dissertation has met all standards of excellence
and scholarship as determined by the faculty.
_____________________________________ _________________________________
Iman C. Chahine, Ph.D. Nikita Patterson, Ph.D.
Committee Chair Committee Member
_____________________________________ _________________________________
Lauren Margulieux, Ph.D. Natalie S. King, Ph.D.
Committee Member Committee Member
______________________________________
Hongli Li, Ph.D.
Committee Member
_____________________________________
Date
_____________________________________
Gertrude Tinker Sachs
Chairperson, Department of Middle and
Secondary Education
_____________________________________
Paul A. Alberto, Ph.D.
Dean
College of Education & Human Development
AUTHOR’S STATEMENT
By presenting this dissertation as a partial fulfillment of the requirements of the advanced
degree from Georgia State University, I agree that the library of Georgia State University shall
make it available for inspection and circulation in accordance with the regulations governing
materials of this type. I agree that permission to quote, copy from, or to publish this dissertation
may be granted by professor under whose direction it was written, by the College of Education
and Human Development’s Director of Graduate Studies, or by me. Such quoting, copying or
publishing must be solely for scholarly purposes and will not involve potential financial gain. It
is understood that any copying from or publication of this dissertation which involves potential
financial gain will not be allowed without my written permission.
____________________________________________________
Solomon A. Betanga,
NOTICE TO BORROWERS
All dissertations deposited in the Georgia State University library must be used in accordance
with the stipulations prescribed by the author in the preceding statement. The author of this
dissertation is:
Solomon A. Betanga
1067 Rowanshyre Circle
McDonough, GA 30253
The director of this dissertation is:
Dr. Iman C. Chahine
Department of Middle and Secondary Education
College of Education and Human Development
Georgia State University
Atlanta, GA 30303
CURRICULUM VITAE
Solomon A. Betanga
ADDRESS: 1067 Rowanshyre Circle
McDonough, GA 30253
EDUCATION:
Ph.D. 2018 Georgia State University
Teaching and Learning/Mathematics Education
Post-Masters Certificate 2018 Georgia State University
Quantitative Research in Education
Master of Science 2013 University of West Georgia
Mathematics
Education Specialist 2011 Liberty University
Teaching and Learning/Mathematics Education
Master of Arts 2009 Mercer University
Teaching/Mathematics Education
Bachelor of Science 1996 University of Buea
Mathematics
Diplomas 1999 National Advanced School of Posts and
Telecommunications-Yaounde Cameroon
Telecommunications Technician Certificate
2009 Georgia Professional Standard Commission
- Clear renewable teaching (T6) certificate
- Gifted certificate
2005 - Pharmacy technician certificate
PROFESSIONAL EXPERIENCE:
2017 – Present Lecturer/Mathematics - Gordon State College
2015 – 2017 Limited tern Assistant Professor of Mathematics
Gordon State College
2014 – Present Adjunct Instructor/Mathematics - Georgia Military College
2018 – Present Adjunct Instructor/Mathematics - Mercer University
2017 - Present Adjunct Online Instructor/Mathematics
Southern New Hampshire University
2017 – Present E-Core Online Instructor/Mathematics-Georgia VIEW
2013 - 2014 Teacher/Mathematics - Bibb Academy of Excellence
2011 – 2013 Coach/Mathematics - Southwest High, Macon Georgia
2010 - 2011 Teacher/Mathematics - Twiggs County High School, GA
2009 – 2010 Teacher/Mathematics - Dutchtown High School,
McDonough Georgia
1996 – 1997 Teacher/ Mathematics - Queen of Rosary College Okoyong
1997 – 2004 Technician /Telecommunications - National Advanced
School of P&T Yaounde - Cameroon
PRESENTATIONS AND PUBLICATIONS:
Lacefield, W. & Betanga, S. A. (2008, October). Integrating Mathematics with Literature. A
paper Co Presented with Dr. William Lacefield of Mercer University at the GCTM
conference in October 2008 at Rock Eagle.
Betanga, S. A. & Patterson, N. (2016, February). “Counting Cube Task”. Paper presentation at
the 29
th
annual Perimeter college mathematics conference.
Betanga, S. A. (2016, March). Increasing students’ engagement, learning and achievement in a
mathematics classroom using teacher-made/web-based videos - the flipped instructional
model. Paper presentation at the STEM conference at Georgia Southern University.
Betanga, S. A. (2016, March). The flipped instructional model- a way to bring activities, inquiry
and discovery learning to the classroom and increase students’ engagement in
mathematics using teacher made/web-based videos. Poster presentation at the 28
th
International Conference on Technology in Collegiate Mathematics in Atlanta
Betanga, A. S. (2016, April). Effective assessment strategies during and after classroom
instruction and how the results can be used to improve students’ performance. Paper
presented at the 6
th
annual conference on Scholarly Teaching at Georgia State University.
PROFESSIONAL SOCIETIES AND ORGANISATIONS
2017 National Education Association
2017 Georgia Education Association
2016 American Mathematical Association of Two-year Colleges
2016 National Council of Teachers of Mathematics
2016 Georgia Council of Teachers of Mathematics
THE EFFECTS OF MATHEMATICAL MODELING INSTRUCTION ON PRECALCULUS
STUDENTS’ PERFORMANCE AND ATTITUDES TOWARD RATIONAL FUNCTIONS
by
Solomon Betanga
Under the direction of Dr. Iman C. Chahine
ABSTRACT
According to Blum (2011), mathematical modelling is the translation between the real
world and mathematics and from mathematics back to the real world. Blum and other studies
Nourallah and Farzad (2012) for example, have indicated that this process of alternating
between reality and mathematics during mathematical activities has impacts on students’
mathematical knowledge.
This study investigated the effects of mathematical modeling instruction on precalculus
students’ performance in a Rational Function Exam (RFE) and their attitudes toward rational
functions. It was an exploratory embedded single case study design using both quantitative and
qualitative methods. A sample of 54 precalculus students enrolled in two sections of
precalculus at a local college in one major southern city of the United States was used for this
study. The two precalculus sections were purposefully selected from five sections, with 24
students in the treatment group and 30 students in the comparison group.
Quantitatively, participants completed a pre-post Rational Function Exam (RFE) and an
Attitude Toward Mathematic Inventory (ATMI) survey (Tapia & Marsh, 2004) before and after
the study. Qualitative techniques were employed to determine the type and cognitive
complexity of representations. These qualitative methods included interviews, a questionnaire,
artifacts of students’ work and the researcher’s memos. The interviews and questionnaire
responses were used to gather demographic and in-depth information about students’
experiences with the method of instruction. ANCOVA and reliability analysis were used to
analyze quantitative data while coding (Saldaña, 2013) was used to analyze qualitative data.
Quantitative analysis results using ANCOVA showed a statistically significant
difference (p < 0.001) between the posttest mean score on the RFE of the treatment group and
the mean posttest score of the comparison group. The ANCOVA results also showed a
statistically significant difference (p = 0.004) between the ATMI mean posttest score of the
treatment group and that of the comparison group.
Qualitative data analysis of the artifacts, interviews, researcher’s memos and the
questionnaire by coding revealed three important themes describing the effects of modeling
instruction on students’ types and cognitive complexity of representations of rational functions:
1) Students tend to have positive views of rational functions and display engaging and immersed
attitudes towards learning mathematics in a modeling instructional setting, 2) teacher’s guidance
during modeling instruction tend to help students’ mathematical representations of functions and
real-world scenarios & 3) mathematical modeling instruction tend to foster critical thinking and
conceptual understanding of rational functions, increasing students’ representations capabilities
and cognitive complexities.
These results suggest that mathematical modeling instruction had positive effects on
students' learning and understanding of rational function concepts, their attitudes towards
learning rational functions and the cognitive complexity of their representations of functions.
INDEX WORDS: Keywords
Mathematical modeling, Mathematical model, Rational function, Function representation,
Attitudes, Cognitive Complexity, Modeling Cycle.
THE EFFECTS OF MATHEMATICAL MODELING INSTRUCTION ON PRECALCULUS
STUDENTS’ PERFORMANCE AND ATTITUDES TOWARD RATIONAL FUNCTIONS
by
Solomon Betanga
A Dissertation
Presented in Partial Fulfillment of Requirements for the
Degree of
Doctor of Philosophy
in
Teaching and Learning
in the
Department of Middle and Secondary Education
in the
College of Education and Human Development
Georgia State University
Atlanta, GA
2018
Copyright by
Solomon A. Betanga
2018
DEDICATION
I thank the Lord Almighty for making it possible for me to get this level of education.
This work is dedicated to my late father Augustine Betanga, my mother Rose Awungngia and
my late uncle Christopher (Kitts) Mbeboh. This Ph.D. achievement would not have been
realized without their support and encouragement. May their souls (dad and uncle Kitts) rest in
perfect peace, Amen.
To my wife Jane Betanga, my daughters Tracy Betanga, Ajong Betanga and my son
Christopher Betanga, thank you for the love, prayers, support and being a wonderful family that
keeps me going. You are my inspiration.
To my siblings: Patricia Morfaw. Esther Betanga, twin sister Caroline Ngenyi Betanga,
Alfred Betanga and Johnson Betanga, thank you for your support, prayers and encouragement.
We are truly blessed to be a wonderful family.
ACKNOWLEDGEMENTS
I would not have completed this dissertation without the expertise, the talents, the
motivation, the guidance and dedication of my adviser - committee chair Dr. Iman Chahine. All
I can say is thank you and may God bless you for all you have done. You never gave up on me.
To my committee members: Dr. Nikita Patterson, Dr. Lauren Margulieux, Dr. Natalie S.
King and Dr. Hongli Li, I thank you for your support, your feedback, your encouragement in
helping me complete this piece of work. I will forever be indebted to you all.
To other faculty members in the department of mathematics education especially my
former adviser Dr. David Stinson, I thank you so much for believing in me and your continuous
support throughout the Ph.D. program.
ii
TABLE OF CONTENTS
LIST OF TABLES……………………………………………………………………………......v
LIST OF FIGURES………………………………………………………………………....…...vi
ABBREVIATIONS ………………………………………………………………………...…. vii
Chapter
1. INTRODUCTION…………………………………………………………………….1
Problem Statement…………………………………………………………………….1
Purpose and Rationale of the Study……………………………………………….......4
Research Questions…………………………………………………………………....5
Null and Alternative Hypotheses……………………………………………….……..5
Definition of Terms……………………………………….…………………………...6
Theoretical Framework………………………………………………………………..7
Significance of the Study…………………………………………………………….13
2. LITERATURE REVIEW………………………...…………………….…………....15
Mathematical Modeling……………………………………………………………...15
Mathematical Models and Representations………………………………………….18
Teachers’ Role in Mathematical Modeling…………………………………………..20
Mathematical Modeling, Lecturing and Problem Solving…………………………...21
Potential Impacts of Mathematical Modeling………………………………………..22
Gaps in the Literature………………………………………………………………...26
Common Methodologies in the Literature…………………………………………...27
Summary of Literature……………………………………………………………….28
3. METHODOLOGY…………………………………………………………………..30
Study Design…………………………………………………………………………30
Study Settings………………………………………………………………………..32
Participants and Sampling Techniques………………………….…………………...33
Data Collection Techniques………………………………………………………….35
Procedure…………………………………………………………………………….38
Fidelity of Implementation…………………………………………………………..44
Data Management……………………………………………………………………44
iii
Data Analysis………………………………………………………………………...44
Validity and Reliability……………………………………………………………....47
Confidentiality and Ethics………………………………...………………………….49
Trustworthiness………………………………………………………………………49
Researchers’ Subjectivity…………………………………………………………….50
Potential Limitations…………………………………………………………………51
4. DATA NALYSIS AND RESULTS………………………………………………....52
Quantitative Data Analysis…………………………………………………………..53
Reliability Analysis…………………………………………………………………..53
Qualitative Data Analysis……………………………………………………………60
Emerging Qualitative Findings ……………………………………………………...63
Summary of Results…………………………………..……………………………...76
5. DISCUSSION…………………………………………………………… ………….77
Major Findings…………………………………………………………………….…77
Situating Findings within the Literature……………………………………………..79
Recommendation for Future Research……………………………………………….84
Limitations…………………………………………………………………………...85
Implications…………………………………………………………………………..86
Conclusion…………………………………………………………………………...88
REFERENCES…………………………………………………………………………………..90
APPENDICES………………………………………………………………………………….108
iv
LIST OF TABLES
Table Page
1. Demographic Data………………………………………………………………….........34
2. Rational Function Concepts on the RFE and Number of Items per Concept………........36
3. Unit objectives, related activity and timeline……………………………………………40
4. Data Collection Procedures…………………………………………………………....…41
5. Differences Between the Treatment and Comparison Groups…………………………..43
6. Coding Protocol for Students’ Representations…………………………………….........47
7. Reliability Analysis of ATMI Instrument………………………………………………..54
8. Descriptive Statistics for RFE Posttest…………………………………………………..54
9. Tests of Normality of RFE Posttest data…………………………………………………55
10. Estimated Marginal RFE Means- Dependent Variable: Posttest………………………...56
11. ANCOVA Results for RFE- Test of Between Subjects-Effects…………………………56
12. Descriptive Statistics- Dependent Variable: ATMI-Posttest……………………… …...57
13. Tests of Normality of ATMI Posttest Data…………………………………...…..……..68
14. ATMI-Estimated Marginal Means -Dependent Variable: Posttest……………………....59
15. ANOVA Results - ATMI-Tests of Between-Subjects Effects- Posttest………………...59
16. Codes, Concepts and Categories…………………………………………………………62
17. Sample Students’ Questionnaire Responses on how They Felt After Instruction…….…64
18. Percentage of Students’ Responses on the ATMI-Survey on Related Issues…………....67
19. Percentage of Students with Partial/Full Credits Scores on the RFE Items……………..69
20. Comparison of Misconceptions between Student 5 and Student 6 on Item 2d of RFE….74
21. Comparison of Problem-Solving behavior of Student #5 and Student #6 on RFE……...75
22. Summary of Results……………………………………………………………………...76
v
LIST OF FIGURES
Figure Page
1. Mathematical modeling cycle adopted from Blum…………………………………….....8
2. Research design-Two groups, random assignment, Pre-test, Post-test………………......32
3. Box plot of RFE posttest data…………………………………………………………....54
4. Assumption of linearity between the covariate RFE-pretest and posttest……...………..55
5. Box plot of ATMI posttest data………………………………………………………….57
6. Assumption of linearity between the covariate ATMI-pretest and posttest……………..58
7. A code-to-theory model for qualitative inquiry. Adopted from Saldana (2013, p. 13) ....60
8. Diagram depicting qualitative data analysis conducted in the study…………………….61
9. Response of student 2 in comparison group………………………………………….….65
10. Response of student 22 in comparison group……………………………………………65
11. Response of student 16 in comparison group…………………………………………...65
12. Response of student 15 in comparison group…………………………………………...66
13. Response of student 25 on questionnaire question……………………………………….71
14. Graph of RFE item 2d…………………………………………………………………… 73
vi
ABBREVIATIONS
ATMI Attitude towards Mathematics Inventory
ANCOVA Analysis of covariance
GSU Georgia State University
IRB Institutional Review Board
NAEP National Assessment of Educational Progress
PISA Program of the International Student Assessment
RFE Rational Function Exam
STEM Science, Technology, Engineering and Mathematics
TIMSS Trends in International Mathematics and Science Study
NSF National Science Foundation
WWC What Works Clearinghouse
vii

1
CHAPTER 1
Introduction
Statement of the Problem
Research studies (Cangelosi et al., 2013; Yee & Lam, 2008; Nair, 2010; Datson, 2009;
Bardini et al., 2014 etc.) indicate that student have a hard time dealing with rational functions.
A rational function is a ratio of two polynomial functions. This means that both the numerator
and denominator are polynomial functions, with the denominator different from zero. For
example, if the function R(x) is a rational function, the R(x) =
, where f(x) and
g(x) are polynomials functions. These are functions taught in precalculus classes to both
mathematics and non-mathematics major students to prepare them for advance courses and
careers.
Cangelosi et al. (2013) indicated that college students enrolled in college algebra and
calculus have misconceptions and make errors with the concept of negative exponential
expressions. Negative exponential expressions are rational functions which many students do
not belief so. For example, (3x + 5)
-1
is a negative exponential expression which is a rational
function of the form
, 0. Yee and Lam (2008) reported that many pre-university
students made many errors in the integration of rational functions which they attributed to
students’ week algebraic skills. Nair (2010) points out that some high school and college
students have an incomplete conception of rational functions, asymptotes, limits and
continuity which often becomes a challenge for their understanding of other mathematical
concepts. Nair also indicates that some students think that rational functions are rational
numbers and some think that a rational function has a number in the denominator instead of a
2
variable. Datson (2009) showed that some students have misconceptions with the concepts of
domain and zeros of rational functions.
Bardini et al. (2014) found that both high school and college students have
misconceptions with mathematical concepts including the concept of a function which plays a
vital role in the understanding of further mathematics sections including calculus and algebra.
The Bardini et al. (2014) study found that many beginning undergraduate students master skills
without any conceptual understanding. The study also showed that out of 383 student
participants, only 62.8% of the students could define and give an appropriate description of a
function, only 41.8% could tell whether a given graph or rule represented a function and up to
15% could not make the connection between function graphs and tables of values.
The 2015 report of the National Assessment of Educational Progress (NAEP) shows
that only 37% of students scored at or above 163 on the NAEP mathematics scale (0 – 300),
which is the indicator for college mathematics preparedness. The same report also indicates a
decline in the average mathematics score of 12 graders compared to the results in 2013. The
average mathematics score for 12 graders was 150 in 2015 compared to 152 in 2013. In the
same report, the mathematics results for Black and Latino students was low. Only 7 percent of
Blacks and 12 percent of Latinos scored at or above proficiency level. The 2017 NAEP report
also show a similar trend in 2015 with no significant change in mathematics scores. Twelve
graders and college students face enormous challenges in mathematics, especially when dealing
with mathematical problem solving involving rational functions.
Another report in 2015 from the Program of the International Student Assessment
(PISA) indicates that students from Singapore, China, Estonia, Hong Kong, Slovenia, Japan,
Korea, Finland, New Zealand, Australia, Canada and Germany continue to outperform students
3
from United States. According to the 2015 PISA results, the United States scored 470 points in
mathematics below the international average score of 490, with Singapore having the highest
score of 564 points. This same report shows a decline in the average three-year trend score of 2
points for American students.
A third and the latest 2015 report of the Trends in International Mathematics and
Science Study (TIMSS) is not so different from those of the PISA and the NAEP for the
United States. The 2015 TIMSS results show East Asian countries (Singapore, Korea, Chinese
Taipei, Hong Kong SAR and Japan) widening their mathematics achievement gap by 48
points ahead of the United States at the twelfth position. In fact, the Center for Education
indicates that Globally, US is 21
st
and 26
th
in Science and Mathematics respectively.
Precalculus students need to have a firm grasp of important concepts of rational
functions, from solving rational equations, rational inequalities, finding domains, asymptotes,
to a full analysis of rational functions, to be successful in the course as well as subsequent
mathematics courses including calculus.
Given these challenges faced by college students in mathematics and particularly
rational functions, according to the Center of Education and Workforce and the National
Science Foundation (NSF), there is a shortage of American students graduating from K-12,
Colleges and Universities equipped with the skills to go into STEM careers such as
Engineering, Medicine, Science, Technology that require them to think critically outside the
box and collaborate to solve different societal problems.
There is therefore, need for student-centered instructional strategies in these institutions
of learning such as mathematical modeling that could help reverse this negative trend on
students’ mathematics achievement at the same time help them understand the world around
4
them using mathematics. According to (Blum, 2011), mathematical modeling is a translation
between the real world and mathematics in both directions that “is meant to contribute to
various mathematical competencies and appropriate attitudes towards mathematics and has the
potential of helping students understand the world around them and have a true picture of
mathematics” (p.19). Despite the positive impacts of mathematical modeling according,
research on mathematical modeling with rational functions is limited or almost non-existence.
This study will provide college, undergraduate students and teachers a research based
instructional strategy (mathematical modeling) that they can employ in the teaching learning of
rational functions, while adding to the existing literature in mathematics.
Purpose and Rationale of the Study
This study investigated effects of mathematical modeling instruction on Precalculus
students’ performance and attitude toward rational functions. Specifically, the purpose of the
study was to find out if there is a statistically significant difference in Precalculus students’
performance as measured by a score on a Rational Function Exam (RFE) between Precalculus
students who received instruction through mathematical modeling and Precalculus students
who received instruction through lecturing. A second purpose was to find out if there is a
statistically significant difference in attitude toward rational functions between Precalculus
students who received instruction through mathematical modeling and counterparts who
received instruction through lecturing. Furthermore, the study explored the nature of the effect
of mathematical modeling instruction on the types and cognitive complexity of representations
used by Precalculus students on rational functions.
The rationale for this was to provide the students with a learning approach that focusses
on critically thinking, interpreting and validation results, when presented with real world
5
scenarios or problems. Precalculus students are going into careers like engineering, nurses,
medicine, science etc. where there will be presented with difficult and complicated situations
such as those involving rational functions. Problems like these require conceptual
understanding of the situation and their ability to rigorously and critically think through and
solve these complicated problems. Such skills are acquired and developed through
mathematical modeling instruction not the traditional lecturing instruction. Furthermore, the
lack of any research on modeling with rational functions was a motivating factor for this study.
Research Questions
The purpose of this study was to investigate the effects of mathematical modeling
instruction on Precalculus students’ performance and attitude toward rational functions. The
following research questions will guide this investigation:
1. What is the effect of mathematical modeling instruction on Precalculus students’
performance as measured by a score on a Rational Function Exam (RFE) and attitudes
toward rational functions?
2. What is the nature of the effect of mathematical modeling instruction on the types and
cognitive complexity of representations used by Precalculus students on rational
functions?
Null and Alternative Hypotheses
H
0
1: There is no statistically significant difference in Precalculus students’ performance as
measured by a score on a rational function exam (RFE) between Precalculus students
who receive instruction through mathematical modeling and Precalculus students who
receive instruction through lecturing.

6
H
a:
There is a statistically significant difference in Precalculus students’ performance as
measured by a score on a Rational Function Exam (RFE) between Precalculus students
who receive instruction through mathematical modeling and Precalculus students who
receive instruction through lecturing.
H
0
2: There is no statistically significant difference in attitude toward rational functions
between Precalculus students who receive instruction through mathematical modeling
and Precalculus students who receive instruction through lecturing.
H
a
: There is a statistically significant difference in attitude toward rational functions
between Precalculus students who receive instruction through mathematical modeling
and Precalculus students who receive instruction through lecturing.
Definitions of Terms
Mathematical Modeling
Blum (2011) defines mathematical modeling as a translation between the real world
(reality) and mathematics in both directions.
Mathematical Model
Blum (2011) defines a mathematical model as equations that result from the
transformation of the real model through mathematization.
Performance
Performance in this study is the students’ score on a Rational Function Exam (RFE).
Attitudes
Gökyürek (2016) defines attitude as the positive or negative response of an individual
toward a certain object, a situation or an event. He considers attitudes to be changeable and
transferable, meaning that a positive attitude can be transformed to a negative attitude and vice
versa. This study is adopting this definition.
7
Representations
Fennel (2006) defines representations as the process of using models (manipulative
materials, graphs, diagrams, and symbols) to organize record and communicate mathematical
ideas. This study will be adopting this definition.
Cognitive Complexity
Robinson (2001) defines cognitive complexity as “the processing demands of tasks and
the availability of relevant knowledge” (p.28).
Theoretical Framework
This study is grounded in the Blum (2011) modeling cycle framework which is the
educational or pedagogical perspective of mathematical modeling whose main idea is to
integrate mathematical modeling into the teaching and learning of mathematics. According to
Blum (2011), mathematical modelling is the translation between reality and mathematics and
from mathematics back to reality. Blum believes that enormous mathematical knowledge as
well as mathematical and modeling competencies is gained through this process. Much of
Blum’s research work is focused on analyzing the cognitive aspects of students ‘work when
they are engaged in mathematical modeling.
The rationale for using the Blum (2011) framework in this study was the fact that it
focused on students’ behavior or attitudes, their actions and their representation of the
mathematical model from the situation model during the modeling process, which could further
explain students’ achievement in modeling and mathematics. These are the variables that this
study was out to investigate. Furthermore, the framework was broken down into smaller and
simpler steps, thus making it easier to examine closely the behavior and thought (cognitive)
processes of the students and teachers when they are engaged in solving problems through
8
mathematical modeling. It was equally a tool that facilitated a close examination of the
different stages of the mathematical modeling process. Precisely, this framework facilitated the
description, the interpretation and the explanation of what goes on in the minds of students and
teachers during a modeling activity. According to Blum and Ferri (2009), the modeling cycle is
very instrumental in the cognitive analysis of a modeling task. This modeling cycle was
therefore helpful in designing the modeling activities for this study as I referred to different
stages involved in the process.
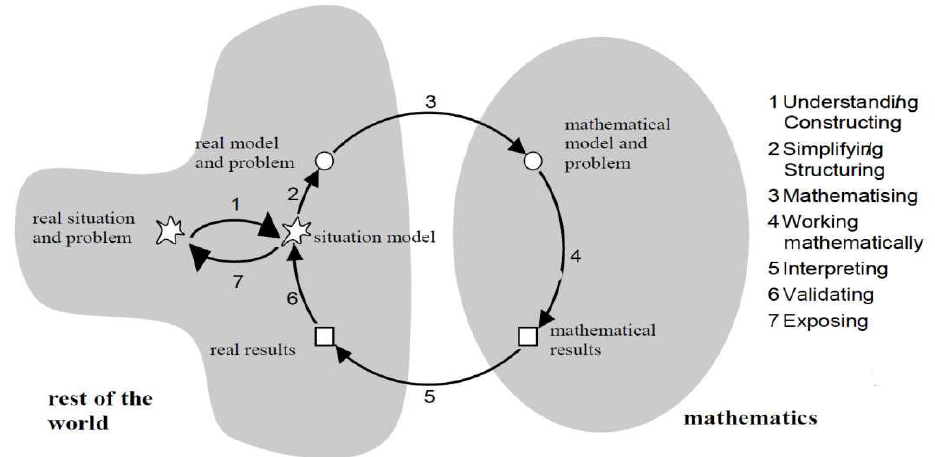
Figure 1. Mathematical modeling cycle. Adopted from Blum (2011, p.18).
The Blum (2011) modeling cycle framework begins and ends with a real-world problem
(situation problem), comprises of seven stages in the modeling process. It is based on the idea
that mathematical knowledge is gained through a translation between the real world and
mathematics and from mathematics to the real world. Blum illustrates this using ‘Giant’s shoes’
and the ‘filling up’ tasks. According to Blomhøj (2008), the role of the modeling cycle as an
educational perspective is for “designing and analyzing tasks with respect to intensions for
students’ learning” (p.11). It is also used for defining mathematical modeling competency as a
9
learning goal. Blum and others in this view, consider mathematical modeling as a means of
learning and acquiring mathematical knowledge.
Nature of Acquiring Mathematical Knowledge from the Framework
The Blum (2011) framework is the educational or pedagogical view that considers
mathematical modeling as a necessary tool to help students acquire mathematical knowledge.
The framework begins with a mathematical task that the students are expected to understand
and look for mathematical relationships that match the situation. As the students establish these
mathematical connections at each step of the modeling cycle, mathematical knowledge is
acquired. Deal (2015) also indicated that there is a connection between mathematical modeling
and algebraic reasoning which occurs during the last five stages of the modeling cycle through
mathematization. This framework was therefore employed as a tool to analyze and understand
students’ knowledge or learning as they navigated through the different stages of the
mathematical modeling process to solve real world problem situations. I will now describe the
process of acquiring mathematical knowledge at the different stages of the modeling cycle.
Figure 1 above shows the steps involved in the modeling process which Blum refers to them as
sub-competencies. The modeling cycle by Weiner Blum shows the relationship between the
real-world and mathematics and vice versa.
The first step of the seven-step modeling cycle begins with the construction of the
situation model from the real-world problem. The construction of this situation model
according to Blum is a demonstration of the understanding of the context of the real-world
problem statement. Imm and Lorber (2013) pointed out that understanding the problem context
in the modeling process is crucial to connecting mathematical knowledge to the real-world
knowledge. At this stage, the modular is trying to make sense of the problem situation. Deal
10
(2015), reported that Blum and Leiss (2007) considered the construction stage to be where the
problem situation is represented in terms of pictures and diagrams to try to understand the
problem. Ferri (2006) considered the situation model as “the mental representation of the
situation (MRS) given in the problem because this best describes the internal processes (mental
picture) of an individual after or while reading the complex modeling task” (p.87). According
to Ferri, the most important phase in the modeling process as pointed out by Blum and Leiss is
the situation model because everyone in the modeling process most go through it and because it
is where understanding of the problem takes place as there is the transition between the real
situation and the situation model. In terms of students’ modeling competencies at this stage,
Blum and Greefrath (2016) indicate that the students at this level construct their own mental
model from a given problem and thus formulate an understanding of the problem.
The second stage of the cycle deals with simplifying and structuring the situation model
making it more accurate and precise, producing the real model of the situation. This is where the
variables are defined, and the assumptions and relationships are made very clearly. Through
simplification and restructuring, the modeling process begins to move from the real-world to the
mathematical world, where mathematizing begins. In terms of students’ modeling competencies
at this stage, Blum and Greefrath (2016) indicate that students at this level are identifying
relevant and irrelevant information from a real problem.
The third stage of the modeling cycle is mathematization. According to Blum (2011),
mathematization enables the transformation of the real model to a mathematical model made up
of equations. All the relevant information of the real model (e.g. data, relations, concepts etc.)
is isolated and put into mathematical statements at level. The mathematical operations in the
real model are performed leading to the production of the mathematical model (equations).
11
According to Yilmaz and Dede (2016), mathematization competencies include identifying
assumptions, identifying variables based on assumptions and constructing mathematical models
based on the relationship among the identified variables. In terms of students’ mathematical
believes, Blomhøj (2008) indicated that “during mathematization and interpretation, the
students’ mathematical beliefs can be unveiled” (p.6). Students translate specific, simplified
real situations into mathematical models (e.g., terms, equations, figures, diagrams, and
functions (Blum & Greefrath, 2016).
The fourth stage of the modeling cycle (working mathematically) deals with solving the
mathematical problem to obtain the mathematical results. Here, the necessary calculations are
made to solve the equations (s). These mathematical results are then interpreted in the context
of the real-world to produce real results during the fifth stage of the modeling process.
During the fifth stage, which is interpretation, Blum and Greefrath (2016) indicate that
students relate results obtained from manipulation within the model to the real situation and
thus obtain real results. This is an indicator of the students’ modeling competency at this level.
At the sixth stage, these real-world results are validated to see if they are consistent with
the mathematical model. The Students according to Blum and Greefrath (2016) judge the real
results obtained in terms of plausibility. Validating the model here means checking whether the
model does what it is meant to do in the real world. If the real results are not valid, meaning if
there are some limitations of the mathematical model, then there is some revision to the model
resulting to a restart of the modeling cycle, where the modular takes a second look at the real-
world problem statement, revise the assumptions and proceed to solving the problem. As the
process continuous, if the mathematical results and real results are valid, then the seventh (last
stage) of the modeling cycle is completed. This is where the modeling results are exposed or
12
published to others. Czocher (2017) indicated that this last step is also known as the
communication stage in other theoretical models. At this exposing stage, the students relate the
results obtained in the situational model to the real situation, and thus obtain an answer to the
problem (Blum & Greefrath, 2016).
Finally, this framework provides some implications for teaching mathematical
modeling, which was helpful in the design and the teaching of the lessons for this study. These
lessons included encouraged students to work actively and independently in creating their own
knowledge of the situation, while guiding them during the process when the need arises. Also,
fostering and encouraging different meta-cognitive activities such as reflecting on their
solutions.
The Framework as a Lens into this Study
The Blum (2011) modeling cycle is a pedagogical perspective of modeling which argues
forcefully for the inclusion mathematical modeling in the teaching of mathematics. It is a
conceptual framework with the purpose of developing students’ understanding of mathematical
concepts as well as the modeling process (Greefrath & Vorhölter, 2016). According to Blum, the
seven steps of the modeling cycle (constructing, simplifying, mathematizing, working
mathematically, interpreting, validating and exposing) represent the steps the students will go
through as they solve a mathematical modeling problem or task. In this study, the modeling cycle
was used to analyze and understand students’ work at every stage of the modeling process. This
framework afforded the opportunity to clearly see and describe what the students are doing, how
they are thinking, their difficulties as the move from one step of the modeling process to the
other. According to Czocher (2017), mathematical cycles allow a focus on cognition and a means
13
for understanding how to trace individuals ‘thinking even though other perspectives for studying
the students’ mathematical learning during the mathematical modeling process do exists.
Leong (2012) indicated that modeling cycles can also be used as a tool for assessing
modeling tasks. Haines and Crouch (2013) indicated that a modeling cycle provides an
opportunity for researchers to describe students’ behavior within the modeling cycle, and by so
doing, they can gain insight into the processes deployed by students when they are faced with
real world problems. At every stage of the modeling cycle, it was possible to evaluate different
modeling sub-competencies and hence the mathematical competencies of the students.
Significance of the Study
Theoretical Significance
Theoretical findings from this study could add to the literature of previously conducted
studies in mathematical modeling (Blum & Niss, 1989; Niss, Blum & Huntly, 1991; Blum et al.
2002; Blum & Leiss, 2005; Blum & Leiss, 2007; Blum & Leiß 2006; Blum & Leiß 2007; Blum
& Ferri, 2009; Blum, 2011; Nourallah & Farzad, 2012 etc.). Furthermore, the focus of this
study on rational functions and modeling instruction, an area of limited or no research is of
unique importance, particularly for teaching undergraduate algebra.
Practical Significance
Practically, this study could provide insight on students’ learning and the teachers’ ways
of teaching rational functions. I argue that using mathematical modeling, students will be more
engaged in learning meaningful connections between the real world and mathematics, instead
of the usual lecturing approach to the learning of mathematics. Furthermore, mathematical
modeling helps students to have a better understanding of the world, supports mathematical
learning including motivation, concept formation, comprehension, retaining, promotes
14
appropriate attitudes towards mathematics and makes mathematics learning meaningful by
revealing the true picture of mathematics to students (Blum, 2011). The study could give
teachers a new approach (mathematical modeling) to teaching rational functions. As a teacher,
this brings new perspective and strategy to the teaching of mathematics and an alternative
approach to guiding students while maintaining a balance between their independence and
guidance as they create their own knowledge.
Finally, this study could have societal, cultural and scientific benefits as well. Since
mathematical modeling deals with real world situations, according to Blum (2002), the real
world are things concerning nature, society or culture, including subjects at all levels, scholarly
and scientific disciplines other than mathematics. Stacey (2015) points out that the use of the
real-world context is an essential part of teaching mathematics for functional purposes and
motivation of the students.
15
CHAPTER 2
Literature Review
The literature review is divided into four sections. The first part of the review will deal
with mathematical modeling. Under mathematical modeling, mathematical models which are
bi-products of the modeling process will be discussed followed by representations of these
mathematical models. I will then follow closely with a discussion of the role of teachers in
mathematical modeling. A distinction between mathematical modeling, lecturing and problem
solving will be highlighted. Potential impacts/benefits of mathematical modeling on the
teaching and learning of mathematics. A review of the gaps in the literature in mathematical
modeling will then follow. The final section will be used to highlight and address the main
methodologies from literature that have been used to study mathematical modeling.
Mathematical Modeling
Blum (2011) defines mathematical modeling as a process involving the translation
between mathematics and the real world in both directions. Blum’s conception of the modeling
process is cyclic (modeling cycle) and he believes that as the students go through the modeling
process (transitioning between reality and mathematics) trying to resolve a mathematical task or
activity, enormous mathematical knowledge is gained. Blum also believes that a particularly
helpful tool for cognitive analysis of the modeling task is the modeling cycle (Blum, 2011; Blum
& Leiß, 2007). He considers mathematical modeling as a means of teaching mathematics and he
calls for effective ways of teaching mathematical modeling (Blum, 2009) which includes having
a good modeling task, encouraging students to apply multiple problem-solving techniques, to
have knowledge of multiple intervention strategies and adequately support the students in the
modeling process.

16
Blum (2011) indicates that the mathematical modeling process (modeling cycle)
involves seven steps to transition from the real world to the mathematical world and vice-versa.
The first step modeling process (modeling cycle) begins with the construction of the
situation model from the real-world problem. The construction of this situation model is a
demonstration of the understanding of the context of the real-world problem statement. At this
stage, the modular is trying to make sense of the problem situation.
The second stage of the modeling process is the simplifying and structuring of the
situation model making it more accurate and precise, produces real model of the situation.
Mathematization is the third stage in the modeling cycle. Mathematization enables the
translation of the real model to a mathematical model made up of equations (Blum, 2011).
The fourth stage of the modeling cycle (working mathematically) deals with solving the
mathematical problem to obtain the mathematical results. The fifth step is interpretation of
results. The sixth step is validating the results and the seventh step is to expose or publish the
results if they are valid.
Studies on mathematical modeling show the existence of different versions of the
modeling cycles by different authors depending on the details and the stages envisage by these
authors (Blum & Niss, 1991; Blum & LeiB, 2007; Blum, 2011; Blomhøj, 2003).
Other definitions of mathematical modeling exist. According to Frejd (2011), many
definitions exist in mathematical modeling depending on the modeling perspective adopted.
Lesh et al. (2013) define mathematical modeling as a process of developing a purposeful
mathematical description or interpretation of a problem-solving situation. Czocher (2017) used
the quadruplet {S, Q, M, R} to define mathematical modeling as “a process of rendering a real-
world problem, Q, as a mathematical problem that can be answered through the analysis of
17
those mathematical statements M. The process creates a relation R mapping the objects and
relationships of the situation S to the mathematical entities M” (p.130). Meyer (2012) defines
mathematical modeling as “an attempt to describe some parts of the real world in mathematical
terms” (p. 1). Dundar et al. (2012) considered mathematical modeling to be the conversion of
real-life situations to mathematical or the conversion from mathematics to real-life situations
that are believable. Confrey and Maloney (2007) also consider mathematical modeling to be the
process of bringing inquiry, reasoning and mathematical structures to transform and solve
indeterminate problem situations, leading to the creation of mathematical models. Despite the
existence these varied definitions, a common theme of mathematical modeling among them is
the relationship between real-life and mathematics which can make a huge impact on students’
attitudes towards mathematics and ultimately their success in mathematics.
The literature in mathematical modeling further suggests the existence of different
perspectives both in the national and international arena. The studies (Aztekin, & Şener, 2015;
Blomhøj, 2008; Kaiser & Sriraman, 2006; Greefrath & Vorhölter, 2016) provide mathematical
modeling perspectives which include 1) the realistic (pragmatic) and applied modeling
perspective with a focus on solving real and authentic problems in industry and science, 2) the
pedagogical (educational) modeling perspective which is process-related (modeling cycle) and
its visualization, as well as content-related goals. Here, modeling is a vehicle for teaching of
mathematics, 3) the socio-critical modeling perspective with the focus of critically examining the
role of mathematics and mathematical models in society, 4) the cognitive modeling perspective
which is focused on scientific goals trying to analyze and understand the cognitive procedures
during modeling 5) the epistemological or theoretical modeling perspective which has theory-
18
oriented goals & 6) the contextual modeling perspective, which is subject-oriented with the
central goal of solving word problems.
Additionally, Niss (2012) highlights the existence of two different views of
mathematical models and modeling in the teaching and learning of mathematics: (1) The idea
that mathematics is for applications, models and modeling and (2) the idea that the learning of
mathematics is for applications, models and modeling. Erbas et al. (2014) echoed similar ideas
about modeling in mathematical education, arguing for modeling as a purpose for teaching
mathematics and the view that modeling is a means to teach mathematics. In the modeling as a
purpose for teaching mathematics perspective, they argue that mathematical modeling is the
basic competency or requirement and the reason for teaching mathematics to ensure that the
students have the necessary tools to be able to solve real world problems in mathematics and
other are fields of study.
Mathematical modeling is not without challenges for some students as they make
connections between reality and mathematics (Blum, 2011). Blum says it so because of the
cognitive demands of the modeling tasks since modeling has connections with other
mathematical competencies such as reading, communicating, designing and applying problem-
solving strategies.
Mathematical Models and Representations
Mathematical models are produced through the process of mathematical modeling. Blum
(2011), indicates that a mathematical model is the outcome of mathematization which is the
transformation of the real model into a mathematical model (made up of equations and variable).
Meyer (2012) defines a model as “an object or concept that is used to represent something else. It
is reality scaled down to a form we can comprehend” (p. 2). Meyer considers a mathematical
19
model as a model consisting of constants, variables, functions, equations, inequalities. Dym
(2004) also considers a mathematical model as a mathematical representation of the behavior of
real devices and objects.
A mathematical modular for a context is a person who introduces from scratch a
mathematical model into that context (Niss, 2012). Niss says that, unlike mathematical modeling
where mathematical models are created from scratch by a modular, application of mathematics
occurs when a mathematical model is already present in a context created by someone else. A
person who investigates or assesses such a model is called a model analyst (Niss, 2012). Li et al.
(2004) are cited Meyer (1985) for highlighting six criteria to be used to evaluate the goodness of
a mathematical model including: accuracy, correct assumptions, precision, robustness, generality
and usefulness.
Representations of a mathematical model, which is a point of focus for this present study
is crucial in students’ understanding of the problem situation. Bostic (2011) indicates that the
representation of a mathematical model influences the procedure that is used to solve the
problem, which further affects the derivations from the analysis of the mathematical model.
Mathematical models, which are created through mathematical modeling, can have different
representations, which may include graphs, equations and tables (Blum, 2011). Fennel (2006)
also adds that models can be represented by manipulative materials, graphs, diagrams, and
symbols. He considers representations as an important part of lesson planning for teachers.
Furthermore, Ainsworth (2014) shows that multiple representations of functions by students have
positive effects on students’ mathematics achievement. According to Ainsworth, learners can
gain deeper understanding when they abstract over multiple representations to achieve insight
into the nature of the representations and the domains.
20
The National Council of Teachers of Mathematics (NCTM. 2000) states, “Representation
is central to the study of mathematics. Students can develop and deepen their understanding of
mathematical concepts and relationships as they create, compare, and use various
representations. Representations such as physical objects, drawings, charts, graphs and symbols
also help students communicate their thinking” (p.280). The National Council of Teachers of
Mathematics (NCTM) process standards for mathematics on representation recommends the use
of representations to model and interpret physical, social and mathematical phenomena.
Teacher’s Role in Mathematical Modeling
For mathematical modeling and the modeling process to be successfully implemented in
the classroom, teachers need to know what they are doing. According to Blum (2011), teachers
are indispensable in students’ mathematics learning. Blum suggests the following principles for
teachers who want to teach mathematical modeling: 1) The criteria for quality teaching should be
considered when teaching modeling, teachers should find a permanent balance between students’
independence and their guidance by their flexibility and adaptive interventions, 2) teachers
should use a broad tasks spectrum for teaching and assessments that cover different topics,
context, competencies and cognitive levels, 3) teachers should support students’ individual
modeling routes and encourage multiple solutions & 4) teachers ought to foster enough student
strategies for solving modeling tasks and stimulate different meta-cognitive activities like
reflection on solution processes and on similarities between different situations and contexts.
Mathematical modeling is relatively new to many teachers. As such, teachers need
professional development to understand the modeling process. Gould (2013) found that many
teachers have misconceptions of the mathematical modeling process and need guidance to help
them understand the modeling process. If the teachers are not well grounded with the
21
mathematical modeling process, then the students will be completely lost. Temur (2012)
indicated that prospective mathematics teachers had difficulties in teaching mathematical
modeling because of lack of experience and training. Huson (2016) pointed out that teachers are
key in implementing the standards, but resources to help them teach modeling are not well
developed. Huson also found that teachers considered modeling to be engaging but had
challenges at some steps of the modeling process especially at the early stage. Furthermore,
Huson recommends more training and resources for teachers to help them understand how to
implement all steps of the modeling cycle in their classrooms. Another study by Wolf (2013)
explored teachers’ concerns with mathematical modeling in the common core standards and the
results showed that teachers were willing to carry out mathematical modeling practices in their
classrooms but had many concerns about time, material and adequate preparation with
professional development. According to Hiltrimartin et al., (2018), many teachers do not
understand that mathematical modeling should come from real world scenarios and requires
making choices and assumptions.
Mathematical Modeling, Lecturing and Problem Solving
West (2013), indicates that while students in the traditional college algebra classrooms
where lecturing is prevalent spend a good amount of time solving for the variables in equations
and inequalities, finding zeros, x-intercepts and y-intercept, students in mathematical modeling
classrooms, approach mathematics holistically with students spending time learning how to
collect, analyze and apply data from real-life situations with the use of technology. According to
West, mathematical modeling instruction is highly student-centered enabling the students to be
engaged and active in the classroom, unlike students in the traditional settings (lecturing) who
are very passive and do not play an active role in the classroom because the teacher is in control
22
of all aspects of the learning. Also, in the traditional setting, problems are less rigorous and there
is little or no collaboration among the students to solve problems. The students rely on the
teacher for the structure and content of the course.
Furthermore, Smith (2013) points out that in the reformed classroom, multiple problem-
solving techniques are used, and the teacher is more concerned with the most efficient way of
solving problems, which is not the case in the traditional setting. Smith also indicated that unlike
reformed instructional approaches, which make use of multiple representations such as tables,
graphs, pictures, symbols and writing, there is frequent use of procedural algebraic techniques to
solve problems in traditional-lecturing instructional classrooms.
For mathematical modeling to be well implemented in mathematics classrooms,
mathematics teachers should distinguish between mathematical modeling and problem solving
Sole (2013) indicated that mathematics educators and curriculum developers have difficulties
distinguishing between a textbook problem, mathematical modeling and problem-solving
exercises. He highlighted six differences between mathematical modeling, problem solving and
textbook in terms of how rigorous they are in modeling, essential and non-essential variables,
number of approaches or techniques used to solve the problem which are wider in mathematical
modeling than in problem solving, differences in mathematical model creation, context of the
problem and validating results.
Potential Impacts of Mathematical Modeling
Blum (2011) indicates that there are potential benefits of mathematical modeling to
students which include: (1) helping students to understand the world around them, (2) supporting
mathematics learning (motivation, concept formation, comprehension and retaining), (3)
contributing in developing different mathematical competencies and attitudes, (4) making
23
mathematics more meaningful and (5) enable students to have a complete picture of
mathematics. Similarly, mathematical modeling has been shown to have positive impact on
students’ attitudes towards mathematics (Wethall, 2011).
Nourallah and Farzad, (2012) show that mathematical modeling at university level has
positive impacts on students’ problem-solving abilities. Similarly, Sokolowski (2015) used the
meta- analytic technique to investigate the effects of mathematical modeling on students’
mathematical knowledge acquisition at the high school and college levels. The study results
showed that modeling helps students with the understanding and application mathematics
Other studies (Mubeen et al., 2013; Mensah et al., 2013; Pawl et al., 2009; Prasad et al.,
2014) indicate that students who are taught mathematics through mathematical modeling tend to
have positive attitudes towards mathematics, hence positive outcomes on students’ mathematical
achievement. According to Popham (2005), students’ attitudes toward a subject can lead to
academic achievement. Teachers, knowledge about students’ attitudes toward a discipline that
they teach is crucial because such information can assist them modify their instructional
strategies to better reach the students.
Also, Saha (2014) says that to educate students, more emphasis should be placed on
developing positive attitude and analytic thinking skills in solving mathematical problems rather
than giving students ready-made problem-solving hints. Mensah et al. (2013) indicate that
teachers’ positive attitudes, radiate confidence in students making them to develop positive
attitude toward the learning of mathematics.
Furthermore, mathematics education currently emphasizes engaging students in
mathematical modeling to understand problems of everyday life and society (Lesh &
Zawojewski, 2007; Sharma, 2013; Vorhölter, Kaiser & Borromeo Ferri, 2014). Vorhölter et al.

24
(2014) highlight the fact that unlike what goes on in the traditional classrooms where students
are learning mathematical concepts and procedures only to pass examinations and forget them
after the exams are over, mathematical modeling will offer the students more than just passing
the examinations by showing them how mathematics will be used in their daily lives. This
strong support for mathematical modeling as an instructional method is gaining worldwide
attention as evident by the participation of about 30 countries around the world including the
top mathematics achieving countries including Singapore, China, Japan, Australia and
Germany at the 2009 14
th
International Conference on the Teaching of Mathematical
Modeling and Applications (ICTMA-14) in Germany (Kaiser, Blum, Ferri, & Stillman, 2011).
Dasher and Shahbari (2015) also indicate that engaging students in modeling activities
helps them learn mathematics in a meaningful way. I believe that if rational functions are
considered as mathematical models of real-life situations, which students can relate to,
students may be motivated to learn and understand mathematical concepts. Kaiser and
Schwarz (2006) indicate that “mathematics should deal with examples from which students
understand the relevance of mathematics in everyday life, in the environment, in the sciences,
and examples from which the students acquire the competencies to enable them to solve real
mathematics problems, those of everyday life, the environment and the sciences” (p.196).
Papageorgiou (2009) points out that students engaged in mathematical modeling
activities express positive views of the modeling process and are pleased that such activities are
connected to real world unlike what they do in their traditional classes. Ellington (2005) show
that modeling-based instruction has a positive effect on students. The results of Ellington’s study
show that students have higher success rate, perform better in common exams, and do slightly
better in a subsequent business and mathematics application course compared to the College

25
Algebra students in the traditional instructional setting. Niss (2012) highlights the fact that
mathematical models and modeling are always needed either implicitly or explicitly whenever
mathematics is applied to issues, problems, situations, and contexts in domains outside of
mathematics. Czocher (2017) point out that when mathematical modeling principles are
emphasized in traditionally taught differential equations course, there is a statistically significant
effect on students’ learning.
Through mathematical modeling, mathematics is used to describe, predict, understand
and prescribe the reality we live in (Blomhoj & Kjeldsen, 2007). Kertil and Gurel (2016)
consider mathematical modeling as a bridge to the STEM education. They believe that
mathematical modeling applications provide students with important local conceptual
developments and meaningful learning of basic mathematical ideas in real situations. Modeling -
based mathematics instruction has a positive impact on the students’ conception of the average
rate of change and their first semester grade in the mathematics course (Doerr et al., 2014).
Bahmaei (2013) indicates that mathematical modeling instruction has greater effect on students’
problem-solving abilities compared to that of students in the traditional classroom environment.
Wedelin and Adawi (2014) show that a good number of students who take
mathematical modeling courses show impressive changes in their abilities to think
mathematically and they also express satisfaction with the mathematical modeling course,
noting that mathematical modeling is an important course in education.
Though mathematical modeling may have positive impacts on the teaching and learning
of mathematics, Freeman (2014) showed that students faced challenges when resolving
mathematical modeling problems because they did not have model development competencies.
Similarly, Blum (2011) highlighted the fact that students around the world have difficulties
26
with modeling tasks as shown by the PISA reports, due to the cognitive complexities of the
modeling tasks.
Gaps in the Literature
Gaps in the literature on mathematical modeling exist in content, methodology, strategies
and frameworks. In the content area, research on rational functions, rational function models and
modeling as well as the teaching and learning of rational functions is very limited as compared to
research on other function models such as linear, polynomial, exponential and logarithmic
models. Furthermore, research in mathematical modeling is heavily focused in the development
and understanding of scientific, engineering, medical and technological models of some real-
world phenomena (Diekmann et al., 2013; León et al., 2008; Magnus et al., 2013; Richard et al.,
2014), but not much is invested towards studying students’ performance or achievement in
mathematics at the undergraduate level.
Because of this heavy focus on scientific models, it also creates a gap in the theoretical
framework as well. Such research studies therefore approach mathematical modeling through the
lens of the realistic (pragmatic) and applied modeling perspective with a focus on solving real
and authentic problems in industry and science (Kaiser, 2005; Pollak, 1968; Kaiser & Schwarz,
2006). There is therefore limited research in the pedagogical (educational) modeling perspective
with the focus on process-related (modeling cycle) and content-related goals (Blum, 2011). The
mathematical modeling methodologies for studying the mathematical content are therefore
limited to a few qualitative and quantitative methods and some case studies. Tao and Hu (2001)
point out that there are few publications on theoretical properties and practical aspects of rational
function models. Freeman (2014) highlights the fact that there are very few research studies on
the effects of mathematical modeling on community college mathematics courses. He however

27
points out the existence of research on the value and efficacy of mathematical modeling in
elementary, secondary and some undergraduate courses. He equally notes the absence of
research on issues related to mathematical modeling in college mathematics courses such as the
modeling process challenges, effective modeling activities, assessment of mathematical
modeling and the students ‘perception of modeling as well as their behavior towards modeling.
Common Methodologies in the Literature
A review of the literature in mathematical modeling reveal a growing list of researchers
have used mixed methodologies involving both quantitative and qualitative methods for the
data collection, data analyses (Coacher, 2017; Freeman, 2014). Some researchers however
have used purely quantitative methods or purely qualitative methods. Doerr et al. (2014) used a
quasi-experimental methodology in their study. Ellington (2005), used purely quantitative
methods to investigate the effects of a modeling-based college algebra course on students’
achievement. Dedrick et al. (2009) indicate in a methodological literature review of 99 articles
in 13 peer review journals that most studies are non-experimental and used non-probabilistic
samples. Their review also indicate that many studies do not report enough information for the
readers to be able to critique the reported analysis.
Aztekin and Şener (2015) employed two content analysis techniques as methodology
for their study. Celik (2017) examined mathematical modeling studies done in Turkey between
2004 and 2015 and results indicated that most of the studies were qualitative with
predominantly purposeful sampling methods used to collect the data. The research design for
this study used content analysis technique. Sokolowski (2015) used the meta- analytic
technique to investigate the effects of mathematical modeling on students’ mathematical
28
knowledge acquisition at the high school and college levels. The study results showed that
modeling help students with the understanding and application of the mathematical concepts.
Prasad and Rao (2014) used a one-way ANOVA to investigate the differences between
positive and negative attitudes toward mathematics for 573 secondary school students. They
found that there were significant differences between them. Their conclusion was that students
want to understand mathematics, but a lack of understanding makes students to have negative
attitudes towards mathematics.
Wilkins and Ma (2003) used hierarchical linear modeling methods to model variations in
students’ rate of change with variables associated with students’ characteristics, instructional
experiences, the environment, variables that affect change at different levels of secondary
schools and variables for the different affective domains (attitudes and beliefs about
mathematics).
Summary of the Literature Review
This study investigated the effects of mathematical modeling as instructional strategy
on Precalculus students’ achievement, representations and attitudes towards rational functions.
The declining trend in the mathematics achievement of American students as indicated by the
TIMSS, PISA and NEAP reports and other research studies compared to other countries
(Singapore, Finland, Germany, China, Korea), calls for student - centered instructional methods
including mathematical modeling. Mathematical modeling has been shown to have some
impact on students’ mathematics’ achievement (Mubeen et al., 2013; Pawl et al., 2009).
Despite the contributions of these studies to the literature on mathematical modeling,
many of them have been focused on other functions like linear, quadratic, exponential
functions, with little or no attention directed towards rational functions. Also, many
29
mathematical modeling studies have been concentrated at the elementary and secondary levels
with very few on college and undergraduate level mathematics. Furthermore, studies on
modeling have largely focused on the pragmatic perspective of mathematical modeling (Kaiser
& Schwarz, 2006), whose goal is to solve real world problems and build mathematical models
for science and engineering purposes. Very few studies have focused on the pedagogical
perspective (Blum, 2011) of modeling that is considered the student’s vehicle for learning and
understanding mathematics. Gaps have therefore, been created in the literature on mathematical
modeling in terms of the content, methodology, strategies and frameworks (Tao & Hu, 2001;
Freeman, 2014). This study seeks to bridge these gaps in the literature, while contributing to the
already existing one in mathematics and mathematical modeling.
30
CHAPTER 3
Methodology
In this chapter, I present a route map of how the study was carried out. This include (a)
the research design, (b) the research setting, (c) the participants and sampling techniques, (d)
the data collection techniques (quantitative and qualitative), (e) the procedure used, (f) the data
analysis techniques (quantitative and qualitative), (g) the data management plan (h) the
researcher’s role in the study, (I) the limitations and finally (j) a summary of the methodology.
The purpose of this study was to investigate the effects of mathematical modeling
instruction on Precalculus students’ performance and attitude toward rational functions. The
following research questions guided the investigation:
1. What is the effect of mathematical modeling instruction on Precalculus students’
performance as measured by a score on a Rational Function Exam (RFE) and attitudes
toward rational functions?
2. What is the nature of the effect of mathematical modeling instruction on the types and
cognitive complexity of representations used by Precalculus students on rational
functions?
Research Design
An exploratory embedded single case study design with both quantitative and qualitative
methods was employed. According to Yin (2014), a case study is “an empirical inquiry that
investigates a contemporary phenomenon in depth and within its real-life context especially
when the boundaries between the phenomenon and context are not evident” (p.16). According to
Yin (2014), a single case study is the best choice when studying just a single group such as a
group of people. The single case here is a group of precalculus students. He distinguishes a case
31
study from an experiment by pointing out that an experiment intentionally separates a
phenomenon from its context, making it possible to only work with a few variables. Yin (2014)
describes a case study as covering contextual conditions that are believed to be relevant to the
phenomenon being studied. This study is thus in line with Yin’s view of a case study in the sense
that it was an in-depth investigation of a contemporary issue in this case, the effects of
mathematical modeling instruction on Precalculus students within a given real-life context.
The rationale for this case study was, therefore, in line with conditions outlined by Yin
(2014) for using a case study, which include the nature of research questions, the extent of
researcher’s role and the extent to which the study is concerned about contemporary issues. This
case study was a single case with embedded units of analysis. Yin further indicates that single
case involves intensive data collection at the same site by a team of investigators. To him, a
single case is analogous to a single experiment. He points out five rationales for a single case
study: (a) when it represents the critical case in testing a well-formulated theory, b) where the
case is an extreme or unique case (c) when the case is representative or typical with the objective
of capturing the circumstances and conditions of an everyday situation d) when the case is
revelatory and (e) when the case is longitudinal (studying the same single case at two different
points in time).
According to Baxter and Jack (2008), Yin puts case studies into three categories:
explanatory, exploratory and descriptive. He considers a case study to be exploratory when it is
used to explore situations in which the intervention being evaluated has no clear, single set of
outcomes. The intervention used in this study is mathematical modeling instruction which does
not have a clear single set of outcomes. Also, the study was exploratory based on the research
question guiding this investigation (Yin, 2014). This study employed quantitative and qualitative

32
techniques. Yin highlights the fact that a case study enables the researcher to gather data from
multiple sources to support the research thesis to guard against construct validity. Data sources
for this study were interviews, the researcher’s memos, a questionnaire, artifacts of students’
work on the pretest and posttest and a pretest posttest RFE and ATMI survey. According to
Hancock and Algozzine (2015), multiple methods are often used when doing a case study
research. To them, the relationship between the design and the method is fundamental to
conducting a successful investigation.
Figure 2. Research design-Two groups, random assignment, Pre-test, Post-test.
Research Setting
This study was carried out at a local college in one major southern city of the United
States. The typical student population at this college is diverse with majority white. On average,
Black students are second to Whites in terms of population, followed by Hispanics. The least
student population is the Asian. It is a four-year college institution with students graduating with
bachelor’s degrees and associate degrees in both the School of Arts and the School of Science as
well as professional degree (e.g. nursing) and has a teacher certification program in the School of
Education. The college offers courses in many major disciplines including Biology, Chemistry,
Mathematics, Education, Physics, Engineering, and Registered Nursing. Many students planning
Treatment Group
Comparison group
Group
Pretest
Treatment
Posttest
33
to take up careers in the nursing, engineering, Biology, business fields are required to register
and obtain at least a ‘C’ grade in Precalculus. The college offers weekend and online classes. The
graduation rate for minority students is low compared to their White counterparts. About 3 in 5
students here use financial aids to cover their tuition and other school expenses. There is one
main campus with other associated campuses at different locations in the state. The school
participates in different sporting events and competitions around the state and beyond.
Participants and Sampling Techniques
The study sample included 54 students enrolled into two precalculus sections based on
their availability (See Table1). These two precalculus sections (24 students in the treatment and
30 students in the comparison) out of five sections were chosen after consultation with the
classroom teachers ensure their readiness teach these two sections using the two instructional
methods. Selection of the sample was therefore accomplished using purposeful sampling
technique in which the classes were selected based on whether the teachers of these classes were
willing and available to implement mathematical modeling instruction and the traditional
instruction in their classes.
Assignment of precalculus sections into treatment and comparison groups was random
even though the students in each section were non-randomly placed in the groups depending on
their availability during the semester. Demographic information in Table 1 below from the
students about their gender, ethnicity and their major (STEM and non-STEM) was obtained
using a questionnaire. Participation in this study was entirely voluntary and the students’ consent
was sought to participate. The teachers who taught the two groups were contacted prior to the
start of the study. After they agreed to participate, the first meeting with the teachers and I was
held to discuss the modalities for the study and after that I met with the teachers individually

34
once a week to discuss the implementation of the instructional methods in their respective
classes.
Table 1
Demographic Data
Group
Gender
Ethnicity
Major
Male
Female
White
Black
Asian
Hispanic
Other
Stem
Non-
Stem
Comp
11
19
17
8
0
2
3
18
12
Treat
12
12
11
6
0
2
5
16
8
Total
23
31
28
14
0
4
8
34
20
Note. N= 54; Comp =Comparison; Treat = Treatment
Table 1 shows that, forty three percent (n= 23) were males fifty seven percent (n= 31)
were females. The number of white participants was twice that of blacks. Whites were 52%,
blacks 26% and Hispanics made up 7%. Fifteen percent of participants identified themselves as
other (mixed race, Caucasians etc.). There were no Asians. Thirty-four participants (63%) were
STEM majors and twenty (37%) were non-STEM majors. Sixteen (47%) of the STEM
participants were in the treatment group and eighteen (53%) in the comparison group.
Participants in both the treatment class and the comparison class completed the same
pre-test and a post-test on Rational Functions (RFE), and the Attitude Toward Mathematics
Inventory (ATMI) survey and a questionnaire. Artifacts of student work on the pretest and
posttest, was collected from both the treatment and groups the comparison groups.
Data Collection Techniques
Both quantitative and qualitative data techniques (instruments) were used for data
collection. Two quantitative (pretest-posttest on RFE and pretest-posttest on ATMI) and three
35
qualitative instruments (questionnaire and artifacts and interviews) were used for data collection.
Quantitative techniques involved the use of a pretest- posttest covering important concepts of
rational functions at the beginning and at the end of the course.
Qualitative techniques were interviews, artifacts (students’ work sheets) on the pre-
posttests and a questionnaire. The questionnaire was used to collect demographic information as
well as their experiences with rational functions before and after their participation in this study.
Interviews were used to collect more detailed and in-depth information about the students’
thoughts and experiences with rational functions. Interviews were also used to follow up on
students’ responses on the questionnaires and their performance on the quantitative posttests.
Robinson (2016) cites Yin (2014) for providing four major principles for data collection
which are a) using multiple sources of data, b) creating a data management plan, c) maintaining a
chain of evidence and d) ensuring that the data is safe. Yin (2014) also indicates that a case study
can be both quantitative where data is numeric and qualitative where data is non-numeric.
Quantitative instruments.
Pretest-posttest. Quantitative data was collected from the pretest, posttest items
on the RFE and the ATMI (Tapia & Marsh, 2004) survey after the students were exposed to
mathematical modeling instruction on rational functions. There were 12 test items on the RFE,
covering specific content areas of representations, equations, inequalities, domain and range,
zeros, asymptotes, and context driven problems as shown on Table 2 below.
Attitude towards mathematics inventory (ATMI) Likert scale survey (Tapia &
Marsh, 2004). The survey is made up of 40-item Likert scale with four subscales (self-
confidence, value, enjoyment and motivation. A confirmatory factor analysis of the ATMI
(Majeed et al. 2013) showed that this scale has a high reliability Cronbach’s alpha of 0.963.

36
Students in both the treatment and control groups completed the ATMI survey (Tapia &
Marsh, 2004) before and after the study, to determine the effect (if any) of the intervention
(mathematical modeling instruction) on students’ attitudes towards mathematics, hence rational
functions.
Table 2
Rational Function Concepts on the RFE and Number of Items per Concept
Concept
Objective
Number of
items
1. Rational function
models(represent
ations)
Students should be able to create rational
function models (graphs, tables, equations)
of real-world phenomena. They should be
able to transform from one models or
representation to another
4
2. Rational equations
Students should be able to solve rational
function equations.
1
3. Rational
Inequalities
Students should be able to solve rational
function inequalities
1
4. Rational function
operations
Students should be able to find the sum,
difference, product and quotient of rational
functions
2
5. Domain and range
of rational
functions
Students should be able to find domain and
range of rational functions
1
6. Zeros of Rational
functions
Students should be able to find the zeros of
rational functions
1
7. Asymptotes
Students should be able to find the vertical
and horizontal asymptotes of rational
functions
1
8. Context driven
problem
Students should be able to solve context
driven problems
1
Total
12
37
Qualitative instruments. To provides answers to the research question two about the
types and level of cognitive complexity of precalculus students’ representation of rational
functions, data from interviews, students’ artifacts, questionnaire and researcher’s memos were
collected and qualitatively analyzed using coding through a web-based application Dedoose.
Questionnaire. To gather information on students’ experiences and thoughts with
on the instructional method used. Questionnaire were given at the end of the study.
Artifacts. To explore students’ representations (written work, tables, graphs and
equations) of functions and mathematical ideas and to make sense of the quantitative
findings, a thorough review of the students’ solutions on the pre-post RFE tests were
examined.
Interviews. To gather more detailed in-depth information about their experiences
with mathematical modeling and rational functions and as a follow up to students’
responses on the questionnaires, 4 students (2 from the treatment and 2 from the
comparison group) were interviewed based on their pretests and posttests scores. The
interviews were conducted outside the regular class time based in the participants’
availability.
Researcher’s Memos. Although formal observation protocols of instruction were
not put in place, I did however make informal visits to the teachers’ classrooms once a
week during which memos about the instruction were taken. These memos were about
the student-teacher interactions, students’ engagement and behavior, teaching strategy,
the type of problems and examples given to students to work on during class. The
memos were used for discussions with the teachers during our meetings to ensure proper
38
implementation of instructional strategy. These memos also gave me a true picture of
what was going in the two classrooms.
Attrition Rate
According to the What Works Clearinghouse (WWC), an initiative of the U.S.
Department of Education’s Institute of Education Sciences, attrition is the loss of sample during
a study for a variety of reasons. Similarly, Amico (2009) considers attrition as the loss of
randomly assigned participants’ data which can introduce bias in the external validity. Thus, the
lower the attrition rate the lower the threat to external validity of a study. Fifty-seven students
consented to participate in this study and took the pretest, but three students did not take the RFE
and ATMI posttests (2 students from the treatment and 1 student from the comparison group).
The three students had withdrawn from the course before the posttests were administered. This
resulted in an attrition rate of 5.3% and a 0% differential attrition rate. Six students (3 from each
group) selected to be interviewed based on their tests scores. Four of the six students volunteered
to be interviewed. The other two students (one from each group) were absent on scheduled dates
for the interviews resulting to an overall attrition rate of 33.3% and a 0% differential attrition rate
for interviews. According to Lewis (2013), overall attrition is the combined attrition rate in the
treatment and the control groups while differential attrition is the difference between the attrition
rate in the treatment group and that in the control group. The WWC standards for overall attrition
rates of below 40% and differential attrition rates below 2% are acceptable levels of bias under
both the liberal and conservative assumptions.
Procedure
The study was conducted over a period of 5 weeks. Before collecting data, I obtained an
approval from the college by submitting a research request application detailing my research
39
proposal to the office in charge of research at the college. An Institutional Review Board (IRB)
approval from Georgia State University was also obtained before beginning data collection for
this study. Once the approvals to conduct the study were obtained, I began to contact teachers to
see those who were willing and prepared to teach the two precalculus sections (treatment and
comparison groups). After securing the teachers’ participation, I began meetings with them to
brief them on the purpose of the study and the how the study was to be carried out. I
continuously met with the teachers individually once a week until the end of the study. First, I
visited their classes to recruit the students and ask for their consent to be part of the study since
participation was entirely voluntary. One precalculus section (n= 24 students) was randomly
assigned to the treatment group while the other section (n = 30 students) was used as the
comparison group.
To ensure proper implementation of the instructional methods, I met with the teachers to
discuss the procedures and agreed upon prior to the start of the study. My meetings with the
teacher of the treatment group were focused on incorporate mathematical modeling strategies in
the classroom and providing extra resources, including different problem types and project
activities that align with the content of the course syllabus to implement in teaching, using
modelling techniques. Two 30-45 minutes training and discussion sessions were conducted with
the teacher of the treatment group during the first week of the study to ensure proper
implementation of the intervention.
Both groups took the same, pre-post RFE and ATMI survey before and at the end of the
study (see Appendix A for RFE items). The data collected from the pretests and posttests was
quantitatively analyzed using a statistical software ANCOVA while coding was used to analyzed
qualitative data from the interviews, questionnaires, researchers’ memos and artifacts of

40
students’ work. The duration of the study was five weeks, starting with the recruitment of
participants, meeting with instructors, data collection and data analysis.
Table 3 below provides a list of content covered during the intervention and a weekly
timeline of implementation.
Table 3
Unit Objectives, Related Activity and Timeline
A questionnaire was given before and after the study to collect demographic information
and to understand how the students felt after learning rational functions through the given
instructional method (mathematical modeling or lecturing).
Concept
Objective
Timeline
1. Rational function
models
Students should be able to create
rational function models (graphs,
tables, equations) of real-world
phenomena. They should be able to
translate from one models to another
Week 1
2. Rational Functions
operations
Students should be able to find the
sum, difference, product and quotient
of rational functions.
Week 2
3. Rational Function
equation and
inequalities
Students should be able to solve
rational function inequalities and
equations
Week 3
4. Domain, range,
zeros, horizontal
and vertical
asymptotes of
rational functions
Students should be able to find
domain and range, vertical and
horizontal asymptotes
Week 4
5. Review, posttests
interviews and
questionnaire
Students review, posttests,
questionnaire and interviews
Week 5

41
Four students (2 from the treatment group and 2 from the comparison group) were
interviewed to gather more information about their experiences with mathematical modeling and
rational functions and to follow up on their questionnaire responses. Table 4 below shows the
data design techniques, data collection instruments and the data analysis techniques for this
study.
Table 4
Data Collection Procedure
Research questions
Design technique
Data collection
instruments
Data
analysis
technique
1) What is the effect of
mathematical modeling
instruction on Precalculus
students’ performance as
measured by a score on a
Rational Function Exam (RFE)
and attitudes toward rational
functions?
Quantitative
RFE- Pre/post
ATMI -Pre/post
ANCOVA
Cronbach’s
alpha for
Reliability
analysis
2) What is the nature of the
effect of mathematical modeling
instruction on the types and
cognitive complexity of
representations used by
Precalculus students on rational
functions?
Qualitative
Artifacts
Interviews
Questionnaire
Researcher’s
memos
Coding
protocol by
Saldaña
(2013)
Differences between the treatment and comparison groups. In the comparison class,
students (n =30) received regular instruction on rational functions which was done through
lecturing, where the teacher was in control of the class explaining rational function concepts to
students on the board. Context was not the central focus. As noted in my memos, there were few
student- teacher interactions as well as student-student interactions. The teacher regularly put
42
notes on the board while the students copy from the board. Very few students asked questions
and during my visits, I did not observe students solving problems on the board. There was less
collaboration, little or no discussions and reflection on solutions. The teacher gave a step by step
approach to solving problems, followed by examples on the board for the students to copy. Many
examples of problems assigned both on the board and from the textbook here involve direct use
of the formulas and were mostly computational in nature. There were neither real-world
application problems nor thought-provoking type problems.
Students in the treatment group (n = 24) were taught rational functions using
mathematical modeling instructional strategies where mathematical modeling principles were
emphasized. Rational functions were contextualized in this class as my memos indicate. For
example, rational functions were viewed as models of some real-world phenomena and real-life
situation problems were transformed into mathematical models to help solve the problem
situation. The teacher approached brought in a more holistic approach to solve problems on
rational functions. This involved making connections with the real-world, mathematics and other
subjects, reflecting on their solutions, collaborating and socially interacting with other students in
the group to make sense of the problem situations. The work load for both groups was the same.
However, the differences between the groups were the instructional methods, teacher prior
teaching experiences, the class meeting time, the number of students in each group, number of
meeting sessions per week.
The instructors in both classrooms were veteran teachers of mathematics with over 20
years of teaching. The treatment group instructor is an assistant professor of mathematics with a
Master of Science degree in Actuarial Science. She has 10 years of teaching high school
mathematics and 13 years of teaching undergraduate mathematics including mathematical

43
modeling. The comparison group instructor is an associate professor of mathematics with a Ph.D.
in mathematics with over 30 years of both undergraduate and graduate levels teaching of
mathematics. Table 5 below summarizes the differences between the two groups for this study.
Table 5
Differences between the Treatment and the Comparison Groups
Before and after the two groups were taught using the different instructional methods, all
the students completed an ATMI Likert scale attitude survey.
A questionnaire was given before and after the study to collect demographic information
and to understand how the students felt after learning rational functions through the given
instructional method (mathematical modeling or lecturing).
Group
Instructional method
Teacher’s
teaching
experiences
Number
of
students
Class meeting
time
Treatment
Mathematical modeling
involving real-word
problems, reflection,
validation of solutions,
collaboration and
making connections
between subjects, the
real-world and
mathematics.
Brainstorming of ideas
M.Sc. Actuarial
Science, 10 years
of high school
and 13 years of
undergraduate
mathematics and
mathematical
modeling
teaching
24
Class met twice
per week on
Tuesdays and
Thursdays for a
total of 3 hours
and 20 minutes,
from 12:30pm to
2:10pm
Comparison
Traditional lecturing
Students listen and copy
notes from the teacher,
Little or no collaboration
and brainstorming of
ideas
Ph.D.
Mathematics,
30+ years of
undergraduate
and graduate
mathematics
teaching
30
Class met three
times per week on
Mondays,
Wednesdays and
Fridays for a total
of 3 hours and 30
minutes, from
8:00am to
9:10am.
44
Four students (2 from the treatment group and 2 from the comparison group) were
interviewed to gather more information about their experiences with mathematical modeling and
rational functions and to follow up on their questionnaire responses.
Fidelity of Implementation.
Triangulation with self-reporting and assistance was used to ensure fidelity of
implementation of the procedures. To ensure that the intervention (mathematical modeling
instruction) was implemented correctly as a method of instruction for rational functions
throughout the study, I visited the teacher’s classroom once a week to observe the instruction.
The teacher also self-reported what went on in the classroom after every lesson and during our
regular meetings. Students’ questionnaire and interview responses related to the instructional
method were also used to assess fidelity of implementation of the instruction.
Data Management
All the data (quantitative and qualitative) collected for this study either digital or paper
was stored in secured locations (keyed and locked cabinets). The data collected was coded to
ensure non-identification of participants. Data from the pretest and the post-test was collected in
the regular classroom stored in a lock and keyed cabinet by the classroom teacher. All Artifacts
of students' work on the pretest post-test were collected in the regular classroom stored in a lock
and keyed cabinet by the classroom teacher. Questionnaire responses were collected in the
regular classroom stored in a lock and keyed cabinet by the classroom teacher.
Both the primary investigator and I had access and transportation of the information.
Institutions that ensured that this study was correctly carried also had access to your information.
They are the GSU Institutional Review Board, the Office of Human Research Protection (OHRP)
and the University Research Services and Administration (URSA) office at GSU.
45
Data Analysis
Unit of analysis. In this study, my unit of analysis (case) is precalculus students. Yin
(2009) considers the unit of analysis in a study to be the case and that it is related to the way the
initial research question (s) is defined. It is what the researcher is trying to analyze in a study,
which could be an individual, a process, a program or even differences between organizations.
Quantitative data analysis. To provides answers to the research question one about the
effect of mathematical modeling instruction on Precalculus students’ performance, data from the
pre-posttest RFE and the ATMI was collected and analyzed using a one-way ANCOVA.
ANCOVA is a statistical technique used test the main and interactive effects of categorical
independent variables on a continuous dependent variable, while controlling the effects of a
continuous confounding variable called the covariate. In this study the independent variable was
the instructional method (modeling and traditional) while the dependent variable was the
posttest. The pretest was the covariate that is being controlled. ANCOVA was appropriate for
this study due to the presence of the covariate pretest whose effect on the dependent variable
could be controlled by ANCOVA to increase the power of the results. By controlling the effects
of the pretests, this helped to put students in both the groups on the same ability before the
intervention. ANCOVA was also used to compare means of posttest scores on ATMI while
Cronbach’s was used to measure the internal consistency of the RFE and the ATMI instruments.
Qualitative data analysis.
Coding. According to Saldaña (2013), “coding is just one way of analyzing
qualitative data and not the only way” (p.2). The data can be interview transcripts; field notes
observations, journals, artifacts, email correspondences, photographs, videos etc. He points out
that “a code in qualitative inquiry is most often a word or short phrase that symbolically assigns
46
a summative, salient, essence-capturing, and /or evocative attribute for a portion of language-
based or visual data” (Saldaña 2013, p.3). Coding and recoding was achieved through Dedoose’s
2017 web-based application.
Saldaña (2013) also indicated that “qualitative codes are essence-capturing and essential
elements of research, that, when clustered together according to similarity and regularity, they
actively facilitate the development of categories and thus analysis of their connections” (p. 8).
The data was coded to identify the different categories, concepts and themes. According to
Saldaña, a theme is an outcome of coding, categorization or analytic refection and coding is a
cyclical process. Saldaña explains that, the first cycle is rarely perfect. The second, third, fourth
cycles etc. of recoding has the responsibilities to further manage, filter, highlight and focus the
salient features of qualitative data record for generating categories, themes, concepts, meaning
and building theory.
Qualitative data analysis with exploratory techniques was used to analyze the data
collected. The qualitative question of this study was answered by collecting and analyzing data
from artifacts (students’ work sheets), students’ interviews, the questionnaire and the
researcher’s memos. Artifacts of students’ solutions on the RFE helped to identify students’
representations of rational functions. The representations of rational function models (graphs,
tables, equations and written) of students from each group were analyzed by looking at the
quality of students’ work based on the strategy and accuracy used to translate from one
representation of the rational function to the other.
To codify according to Saldaña (2013), is to apply and reapply codes to qualitative data.
He further distinguishes codes and themes by arguing against the recommendations of some
researchers that one should initially code for themes. He says that a theme is not something that

47
is coded, but an outcome of coding, categorization or analytic reflection. The number of codes
one generates depends on many contextual factors including the nature of one’s data, the coding
method as well as how detailed one wants to be. The coding scheme in Table 6 below shows
how students’ representations were coded.
Table 6
Coding Protocol for Students’ Representations
Representation
Category
Description
1. Table
A
Any chart or table that is used to organize data
2. written
B
Any word or phrase used to represent any thought,
numbers or mathematical idea
3. Equation
C
Any expression that consist of numbers or symbol or
both
4. Graph
D
A pictorial representation numbers, value or real-world
scenario
5. Mixed
E
Use of table, graph and equation and verbal
Validity and Reliability
Internal Validity. This is a measure of the soundness of the research. Lewis (2013) cited
Shadish et al. (2002) for indicating that a study has internal validity when the causal relationship
between two variables is properly demonstrated. Internal validity is making sure that with the
research done right? It is related to the number of confounding variables in the experiment. The
lower the confounding variables the higher the internal validity, which is expected. To ensure the
validity of the study, I worked closely with the Primary Investigator of this research as well as
48
the teachers to ensure that all procedures are well implemented to reduce confounding variables
and increase the validity of the study.
External Validity. This deals with the study findings to see if the study results can be
generalized to other persons and settings (Lewis, 2013). According to Yin (2014, p. 47), to have
a high-quality case study design means responding to four tests. The tests include, (1) construct
validity, which means identifying the correct operational measures for the concepts being
studied; (2) internal validity, which means to seek to establish a causal relationship, whereby
certain conditions are believed to lead to other conditions, as distinguished from spurious
relationships; (3) external validity, which means defining the domain to which a study findings
can be generalized; and (4) reliability, which means to demonstrate that data collection
procedures for the study can be repeated with the same outcome. Yin (2014) also indicates that
construct validity can be achieved through collecting multiple sources of evidence, establishing a
chain of evidence.
Saltkind (2009) indicates that “the reliability (or consistency) and validity (or the does-
what-it-should qualities) of a measurement instrument are essential because the absence of these
qualities could explain why you act incorrectly in accepting or rejecting your research
hypothesis” (p.109). He further says that reliability and validity are a researcher’s first line of
defense against incorrect conclusions, “if the instrument fails, then everything else down the line
fails as well.” While reliability happens when a test measures the same thing repeatedly resulting
in the same outcomes, validity is concerned with making sure the test or the instrument measures
what it was intended to measure. Validity is about the results of a test not about the test itself.
Robinson (2016) quoted Trochim (2006) for arguing that “in a single case design, there
are 4 threats to internal validity concerning pre/post test data which are history, maturation,
49
testing and instrumentation” (p. 74). Steps were taken in this study to protect against these
threats. The pre-posttest (RFE) was tested for internal reliability using Cronbach’s alpha.
For the reliability of the ATMI survey, the instrument shows a reliability Cronbach alpha
of 0.963 (Tapia, 1996). According to Tapia and Marsh (2004), a factor analysis of the 40-item
scale consisting of four subscales (self-confidence, value, enjoyment and motivation) showed
good internal reliability and indicated stability over time of the test retest. The data also showed
a high level of reliability of the subscales.
Confidentiality and Ethics
Robinson (2016) highlighted the fact that Yin (2014) talks of using precaution to collect,
use and store the data. Keeping participant information secured and ensuring the safety of
subjects is crucial in a research study and this study was not different. All the confidentiality and
ethics rules governing research studies were upheld during this study. To ensure that the rights of
participants were not violated during this study, all personal information of participants was
confidentially kept and not used. The participants’ name and other important information was not
revealed using codes throughout the study.
Trustworthiness
The quantitative data collection methods and analysis presented above were conducted
with all the ethical considerations in mind. For the qualitative data collection and analysis, Cope
(2014) highlighted five criteria for establishing the trustworthiness of qualitative research which
include (1) credibility - the truth of the data or research findings, (2) dependability- the
consistency of the research findings under similar conditions by a different researcher, (3)
confirmability- the ability to demonstrate that the data represents the students’ viewpoints and
not those of the researcher, (4) transferability – the application of findings to other settings or
50
groups and (5) authenticity – the ability and extend to which the researcher expresses the
emotions and feelings of participants’ experiences in a faithful manner. These criteria were met
using triangulation of multiple data sources involving the test scores, students’ artifacts,
interview responses in the students’ own words, the researchers’ memos, questionnaire
responses, and the self-reports from teachers.
Researcher’s subjectivity
I am currently a lecturer of mathematics at the same college where this study was
conducted. As a student in a mathematics classroom and a mathematics instructor for more than
15 years, I have realized the importance of introducing and creating mathematics classroom
activities in the real-world context and giving the students the opportunity and time to explore
these real-world phenomena under the guidance of the teacher. The students’ active participation
in developing their competencies as they think through these problems and formulate strategies
to solving them, plays a vital role in their success in mathematics, especially when dealing with
problems and concepts that students appear to struggle with such as rational functions. I believe
that teachers should engage the students through different instructional strategies including
mathematical modeling which I am investigating its effects on precalculus students’ performance
in this study.
As the researcher also, I oversaw the overall data collection process which included the
recruitment of participants (teachers and students), provided the students with consent forms
before participation. I ensured that all the data collection techniques and instruments were
properly implemented including administering the pre-posttest (RFE), the ATMI survey and the
research questionnaire. With input from some precalculus instructors at the college, including the
teacher participants in this study, I created the rational function exam using the precalculus
51
common final exam questions as a guide and template to ensure the validity of the questions in
the RFE. I met with the teachers of both groups once a week for 30-35 minutes to discuss the
memos progress of instruction in their classes. The memos written during my unofficial visits to
the teacher’s classes were also discussed during my meetings with the instructors. After the data
collection, I proceeded to analyzing the data from the assessments to determine whether there
was a significant difference between the performance and attitudes of precalculus students who
were taught rational functions through mathematical modeling and those who were taught
rational functions through the traditional lecturing method. I equally ensured that the data
collected for this study was kept confidential and in safe locations to maintain privacy of
participants involved in the study.
Potential Limitations
The study had several potential limitations, which should be taken into considerations
when looking at the results.
1. The fact that the different sections of the precalculus (rational functions) were taught by
different instructors may or may not have had the teacher effect on the outcome of this
study.
2. The sample size was affected by subject attrition as participants eventually dropped out
of the study due to withdrawal from the course before the posttests. The attrition rate for
both the RFE and ATMI was 5.3% and 33.3% for the interviews.
3. Cognitive complexity is a psychological variable that can have different meanings or
definitions and hence not easy to measure or quantify
52
CHAPTER 4
Data Analysis and Results
The purpose of this study was to investigate the effects of mathematical modeling
instruction on precalculus students’ performance and attitude toward rational functions. The
intervention for this study was mathematical modeling as an instructional method. The design
was exploratory embedded single case, with both quantitative and qualitative methods employed
to collect and analyze the data. The following research questions and hypotheses were used for
the investigation:
1. What is the effect of mathematical modeling instruction on Precalculus students’
performance as measured by a score on a Rational Function Exam (RFE) and
attitudes toward rational functions?
2. What is the nature of the effect of mathematical modeling instruction on the types
and cognitive complexity of representations used by Precalculus students on rational
functions?
The null hypotheses were as follows:
H
0
1: There is no statistically significant difference in Precalculus students’ performance as
measured by a score on a rational function exam (RFE) between Precalculus students
who receive instruction through mathematical modeling and Precalculus students who
receive instruction through lecturing.
H
0
2: There is no statistically significant difference in attitude toward rational functions
between Precalculus students who receive instruction through mathematical modeling
and Precalculus students who receive instruction through lecturing.
53
The study employed both quantitative and qualitative data techniques for data collection.
Quantitative techniques included a pretest- posttest RFE covering important concepts of rational
functions and a pretest -posttest ATMI survey. Qualitative techniques were interviews, artifacts
on the posttests and a questionnaire. Quantitative data was analyzed using a one-way ANCOVA
and Cronbach’s alpha for reliability analysis while qualitative data was analyzed using coding
protocols according to (Saldaña, 2013) through Dedoose’s 2017 web-based application.
Quantitative Data Analysis
To provide answers to the research question one about the effect of mathematical
modeling instruction on Precalculus students’ performance and attitudes towards rational
functions, data from the pre-posttest RFE and the ATMI was analyzed using a one-way
ANCOVA. The first null hypotheses for question one (H
0
1) which states that there is no
significant difference between the average performance score on a rational function exam
(RFE) between the treatment and comparison groups was tested using a one-way ANCOVA.
ANCOVA was also used to test the second null hypothesis that there is no statistically
significant difference in attitude toward rational functions between the treatment and
comparison groups. Before using a one-way ANCOVA, the data was tested for the
assumptions to ensure that the data was appropriate for use with a one-way ANCOVA.
Reliability Analysis. Before using ATMI survey instrument, a reliability analysis was
conducted using Cronbach’s alpha to ensure the internal consistency of the instrument. Cortina
(1993) points out that a Cronbach’s alpha level greater than 0.70 is acceptable for the reliability
of the instrument. Table 7 below summarizes the Cronbach alpha value calculated for the
pretest and posttest in both the treatment and comparison groups, showing that the ATMI

54
instrument was a reliable instrument for this study given that the Cronbach’s alpha was greater
the .70 for both the pretest and posttest in both groups.
Table 7
Reliability Analysis of ATMI Instrument
Testing the null hypothesis for RFE using ANCOVA-H
0
1
Table 8
Descriptive Statistics for RFE Posttest – Dependent Variable
Group
M(SD)
N
Treatment
45.54 (16.14)
24
Comparison
21.23 (11.71)
30
Total
32.04 (18.35)
54
Note. M = mean. SD = standard deviation
Testing the Outliers’ Assumptions for ANCOVA on the RFE
Figure 3. Box plot of RFE posttest data.
Figure 3 above shows that there were no outliers in the RFE posttest data of the treatment
and comparison groups. Therefore, the outlier assumption was met.
Pretest-
Comparison
Posttest-
Comparison
Pretest-
Treatment
Posttest-
Treatment
Cronbach’s alpha
.74
.78
.71
.72

55
Testing the Assumption for Equality (Homogeneity) of Error Variances
The Levene's Test of equality of error variances was conducted on the Posttest which
Showed a non-statistically significance value of 0.62 (p>.05). This indicated that there was no
significant difference between the variances of the posttest score of the treatment and
comparison group. Therefore, the equal variances assumption was met.
Testing the Normality Assumptions for ANCOVA on the RFE
Table 9
Tests of Normality of RFE Posttest Data
Kolmogorov-Smirnov
Shapiro-Wilk
Group
Statistics
df
P
Statistics
df
p
Posttest
Treatment
.11
24
.20
.97
24
.569
Comparison
.11
30
.20
.96
30
.373
Note. *p < .05 indicates significance
Table 9 shows a non-statistically significant Shapiro-Wilk value (p >.05) for the
normality test in both the treatment and comparison groups. This means that the posttest data for
both groups were normally distributed. The normality assumption of data was met.
Testing the Assumption of Linearity between the Covariate RFE Pretest and Posttest
Figure 4. Assumption of linearity between the covariate (RFE pretest) and RFE- posttest.

56
Table 10
Estimated Marginal RFE Means- Dependent Variable: Posttest
95% CI
Group
M
Std. Error
LL
UL
Treatment
45.90
2.05
41.79
50.01
Comparison
20.94
1.83
17.27
24.62
Note. M=mean; LL = lower limit; UL = upper limit.
Table 10 shows and estimated marginal (adjusted mean) posttest mean of 45.9 for the
treatment group and 20.9 for the comparison group, when the pretest scores were controlled as
covariate. The adjusted posttest mean for the treatment group was 25 more than that of the
comparison group.
Analysis of Covariance
Table 11
ANCOVA Results for RFE-Test of Between Subjects-Effects: Dependent variable- Posttest
Source
df
Type III SS
MS
F
P
Partial Eta
square
Corrected Model
2
12715.23
6357.61
63.27
.000
.713
Intercept
1
3642.85
3642.85
36.25
.000
.415
Pretest
1
4836.63
4836.63
48.13
.000
.486
Group
1
8292.48
8292.48
82.53
.000*
.618
Error
51
5124.70
100.48
Total
54
73264.00
Corrected Total
53
17839.93
Note. *p < .05 indicates significance; SS = sum of squares; MS = mean square
Table 11 above shows a statistically significant group difference (p < .001), eta square =
.618. Therefore, the null hypothesis (H
0
1) was rejected indicating that there was a statistically
significant difference in Precalculus students’ average performance in a Rational Function Exam
(RFE) between Precalculus students who receive instruction through mathematical modeling (M

57
= 45.54, SD = 16.14) and Precalculus students who receive instruction through the traditional
lecturing approach (M = 21.21, SD = 11.71). This test results were consistent with the data
collected.
Testing the Null Hypothesis for ATMI Using ANCOVA- H
0
2
Table 12
Descriptive Statistics for ATMI Posttest- Dependent Variable
Group
M(SD)
N
Treatment
129.67 (12.40)
24
Comparison
120.54 (12.00)
30
Total
124.75 (12.91)
54
Note. M = mean. SD = standard deviation
Table 12 shows the average ATMI posttest score of the treatment group to be 129.67
greater than that of the comparison group with an average score of 120.54. This gives a mean
difference of 9.13.
Testing the Outliers’ Assumptions for ANCOVA on the ATMI
Figure 5. Box plot of ATMI posttest data.
Figure 5 shows that there are no outliers in the ATMI posttest data of the treatment and
comparison groups. Therefore, the outlier assumption was met.

58
Testing the Assumption of Equality (Homogeneity) of Error of Variances
The Levene's Test of equality of error variances was conducted on the ATMI Posttest
which showed a non-statistically significance value of 0.30 (p>.05). This indicated that there
was no significant difference between the variances of the ATMI posttest score of the treatment
and comparison groups. Therefore, the equal variances assumption was met.
Table 13
Tests of Normality of ATMI Posttest
Kolmogorov-Smirnov
Shapiro-Wilk
Group
Statistics
df
P
Statistics
df
p
Posttest
Treatment
.11
24
.20
.98
24
.785
Comparison
.11
30
.20
.94
30
.123
Note. *p < .05 indicates significance
Table 13 shows a non-statistically significant Shapiro-Wilk value (p>.05) for the
normality test in both the treatment and comparison groups. This means that the posttest data
for both treatment and comparison groups was normally distributed. The normality was met.
Testing the Assumption of Linearity between the ATMI Covariate Pretest and Posttest
Figure 6. Assumption of linearity between the covariate (ATMI-pretest and posttest.

59
Figure 6 shows that the assumption of linearity between the covariate (pretest) and the
dependent Variable (posttest) for each Level of the Independent Variable was met.
Table 14
Estimated Marginal ATMI Means- Dependent Variable: Posttest
95% CI
Group
M
Std. Error
LL
UL
Treatment
129.29
2.07
125.13
133.44
Comparison
120.86
1.91
117.02
124.71
Note. M=mean; LL = lower limit; UL = upper limit.
Table 14 shows and estimated marginal (adjusted mean) ATMI posttest mean of 129.29
for the treatment group and 120.86 for the comparison group, when the pretest scores were
controlled as covariate. This indicates an adjusted mean difference of 8.43 between the treatment
and the comparison groups.
Analysis of Covariance
Table 15
ANCOVA Results for ATMI-Test of Between Subjects-Effects: Dependent Variable- Posttest
Source
df
Type III SS
MS
F
P
Partial Eta
Square
Corrected Model
2
3491.85
1745.92
17.08
.000
.411
Intercept
1
1610.21
1610.21
15.75
.000
.243
Pretest
1
2414.39
2414.39
23.61
.000
.325
Group
1
914.29
914.29
8.94
.004*
.154
Error
51
5009.91
102.24
Total
54
817755.00
Corrected Total
53
8501.75
Note. *p < .05 indicates significance; SS = sum of squares; MS = mean square
Table 15 shows a statistically significant group difference F (1, 51) = 8.94, (p =.004), Eta
square = .154. Therefore, the null hypothesis (H
0
2) was rejected indicating that there was a

60
statistically significant difference in Precalculus students’ average attitude score on an ATMI
survey between those who received instruction through mathematical modeling (M = 129.62, SD
=12.40) and those who receive instruction through the traditional lecturing (M =120.54, SD =
12.00). This test results were consistent with the data collected.
Qualitative Data Analysis
Qualitative data for this study was collected from students’ artifacts, interviews,
questionnaire and researcher’s memos. The data was coded through Dedoose’s 2017 web-based
application guided by Saldaña (2013) coding protocols. Figure 7 below shows the coding process
from codes to categories to concepts and themes according to Saldana (2013) that was adopted
for this study.
Figure 7. A code-to-theory model for qualitative inquiry. Adopted from Saldana (2013, p. 13).
According to Saldaña (2013), the first cycle is hardly perfect but the second, third, fourth
cycles etc. manages and filters the qualitative data generating categories, themes, concepts,

61
meaning and building theory. He considers a theme as an outcome of coding and categorization
or analytic reflection.
Dedoose ‘s 2017 web-based application which was then used to analyze the data, has the
ability of integrating qualitative data with quantitative data analyzing the data in great depths,
producing codes, categories and themes. Cates (2018) indicates that Dedoose allows for
qualitative data to be coded through traditional qualitative analysis methods and linking the data
to force-choice quantitative data. Figure 8 below shows the qualitative data analysis process
involved.
Figure 8. Diagram depicting qualitative data analysis conducted in the study.
In the first coding cycle, the data was the raw qualitative data from the four sources
(interviews, artifacts, and questionnaire and research memos). As such, the first codes were the
first striking ideas in the data. The following 45 codes were noted during this first round: (1)
Graphs, (2) encouragement, (3) difficulties, (4) helpful methods, (5) equations (6) real word
application problems, (7) confidence, (8) rational functions are hard, (9) Challenging word
problems, (10) prior knowledge, (11) teaching method, (12) teacher guidance, (13) struggle to
understand, (14) asymptotes (15) motivation, (16) expectations, (17) domain of functions
(18)reflecting on problems, (19) engaging, (20) better understanding after intervention, (21)
Interviews
Artifacts
- Codes
- Categories
- Concepts
Themes
Questionnaire
Researcher’s memos

62
struggling, (22) procedure, (23)concentration, (24) focused, (25) importance of the lesson, (26)
collaboration, (27)students’ attitude on different problems, (28)attitudes toward graphs, (29)
modeling instruction, (30)attitudes towards equations, (31) conceptual understanding, (32)
practice many problems, (33)critical thinking, (34)optimistic, (35)misconceptions, (36) reluctant
to give up (37) passionate, (38)lacks basic algebraic skills, (39) high level thinking skills, (40)
progress, (41) successful, (42) accuracy and procedure on representing a function as graph or
equation, (43) attitudes toward word problems, (44) intercepts of functions, (45) Range.
Recoding the initial codes, and continuing through four recoding cycles, resulted to more
refined codes as redundant words were removed, and others combined into categories and
concepts and then to themes. Table 16 below shows emerging codes, concepts, and categories.
Table 16
Codes, Concepts and Categories
Codes
Concept representation
Categories
Critical thinking, reflection, Confidence,
engagement, motivated, passionate,
Attempts challenging word problems,
Misconceptions, struggles to understand,
lacks basic algebraic skills,
Attitudes towards
learning mathematics
Students’ perception of
mathematical modeling
instruction
Chart, data organizer
Table
Students’
representations and
cognitive complexity
Any word, phrase, any thought, A
mathematical idea
Written
An expression consisting of numbers or
symbol or both
Equation
A pictorial representation numbers, value
or real-world scenario
Graph
Applies more than one representation,
Multiple representation
63
Categories
Two main categories (students’ perception of mathematical modeling instruction and
students’ representations and cognitive complexity) as shown in Table 16, were developed to
provide answers to the qualitative research question 2 on the students’ representations. The
Students’ perception of mathematical modeling instruction category encompassed concepts and
codes of patterns related to student’s behavior and attitudes towards learning mathematics,
specifically rational functions. The students’ representations and cognitive complexity category
was a grouping of codes and concepts of students’ representation of rational functions as
reflected in their artifacts, interviews, questionnaire and researcher’s memos.
Emerging Qualitative Findings
From codes, categories and concepts and repeated examination of these data sources,
three themes emerged (one from the students’ perception of mathematical modeling instruction
category and 2 from the students’ representations and cognitive complexity category). From the
students’ perception of mathematical modeling instruction category, the theme that emerged
was that students tend to have positive views of rational functions and display engaging and
immersed attitudes towards learning mathematics in a modeling instructional setting.
From the students’ representations and cognitive complexity category the themes that
emerged were: 1) Teacher’s guidance during modeling instruction tend to help students’
mathematical representations of functions and real-world scenarios & 2) mathematical
modeling instruction tend to foster critical thinking and conceptual understanding of rational
functions, increasing students’ representations capabilities and cognitive complexities. The next
section is a description of each of the four themes in detail with excerpts of students’ artifacts,
interviews, questionnaire and researcher’s memos.

64
Students’ Perception of Mathematical Modeling Instruction Category
Theme 1: Students tend to have positive views of rational functions and display
engaging and immersed attitudes towards learning mathematics in a modeling
instructional setting. From the interview responses of 4 students (2 from the treatment group
and 2 from the comparison group), three of the students indicated that they had a better
understanding of rational functions than they did before the instruction on rational function.
One student from the comparison group indicated that she still did not like rational functions.
Similarly, when asked in the questionnaire to describe their feelings after the lessons on
rational functions, 19 students (79.2%) of the students in the treatment class stated that the felt
better compared to 14 students (46.7%) in the comparison class (see Table 17 below).
Table 17
Sample Students’ Questionnaire Responses on how they Felt After Instruction
Treatment group
Comparison group
Question
Student
ID#
Response
Student
ID#
Response
How do
you feel
about
rational
functions
now after
the lessons
you just
received?
5
Comfortable
2
I am still a bit
confused
16
I feel that I
understand Rational
functions better now
than originally
learned
22
I still do not like the
topic and now I am a
little more confused.
15
Pretty okay, I
understand the
basics
10
Still do not like
them. They are
difficult
8
Better, just need to
study more
11
Still need more help
3
Ok
5
They are still
difficult to
understand

65
The students were given pseudonyms in the form of ID numbers to protect their
privacy. Figures 9, 10, 11, and 12 below are excerpts of the students’ responses.
Figure 9. Response of student 2 in comparison group.
Figure 10. Response of student 22 in comparison group.
Figure 11. Response of student 16 in Treatment group.

66
Figure 12. Response of student 15 in Treatment group.
Further indication of student’s feelings about rational functions after mathematical
modeling was noted on students’ responses to the ATMI survey. On specific items on the
survey, when asked in Item 37 whether the students were comfortable expressing their own
ideas on how to look for a solution to a difficult problem in mathematics, 70.8% strongly agreed
in the treatment class while only 15 (50%) strongly agreed. The response was similar in item 38
when the students were asked if they were comfortable answering questions in a mathematics
class. In the treatment group 83.3% strongly agreed compared to 47.7% in the comparison
group. Further examination of all the responses on ATMI on issues related to the value of
mathematics, engagement and confidence and motivation was done. Their responses showed
that a higher percentage of students in the treatment strongly agreed (score of 5) on the issues of
motivation, the value of mathematics, engagement and confidence. For example, on the survey
statement of students having a lot of self-confidence with mathematics (see ATMI in Appendix
B- item 17), 20.8% of the students strongly agreed in the treatment class compared to only 6.7 %
of the students in the comparison class. On the issue of enjoying doing mathematics in school
(item 24), 8.3% strongly agreed in the treatment group compared to only 3.3% of students in the
comparison group. According to Tapia and Marsh (2004), the ATMI survey is a 40-item

67
inventory Likert scale type survey. The items are grouped into subscales: Self- confidence items
(9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 40), value items ( 1, 2, 4, 5, 6, 7, 8, 35, 36,
39), enjoyment items (3, 24, 25, 26, 27, 29, 30, 31, 37, 38) and motivation items (23, 28, 32, 33,
34). Table 18 below summarizes the percentage of students’ responses in both groups when on
issues of self-confidence, motivation, value mathematics and enjoyment.
On the issue of valuing mathematics, students in the comparison group scored higher
(34.5%) compared to those in the treatment group (31.4%) even though they were less motivated
and had less confidence in mathematics than those in the treatment group.
Table 18
Percentage of Students’ Responses on the ATMI-Survey on Related Issues
Issue
Survey items
% of students’ score
Treatment group
Comparison group
Self- confidence
9, 10, 11, 12, 13,
14, 15, 16, 17, 18,
19, 20, 21, 22, 40
35.2
33
Value
1, 2, 4, 5, 6, 7, 8,
35, 36, 39
31.4
34.5
Enjoyment
3, 24, 25, 26, 27,
29, 30, 31, 37, 38
25.8
20.6
Motivation
23, 28, 32, 33, 34
13.4
10.9
Table 18 shows that the percentage of students’ scores was higher in the treatment
group in all categories except the value of mathematics. As such, an engaging and motivating
68
instructional strategies such as mathematical modeling could play an important role in the way
students feel and learn mathematics as seen in the case of students in the treatment group.
To further illustrate students’ immersed attitudes in a modeling environment, and to add
depth to the quantitative results, I closely examined the students’ written solutions on each item
on the RFE in both groups to identify the errors or misconceptions made in solving the
problems. This was done to determine whether the student met the learning objectives outlined
in Table 3 above. According to Blum (2011) the modeling process (cycle) begins with
understanding the problem situation and being able to construct the context of the situation.
This is also true with any mathematical problem-solving strategy which begins by the
understanding of the situation at hand before trying to solve the problem. If a student does not
demonstrate understanding of the problem situation, it becomes clear that the student is not
going to employ the right strategy to solve the problem. Therefore, to analyze the students’
solutions on the RFE, I checked for understanding of the problem situation as the first step. I
also focused on the problem-solving strategy and the accuracy of the final answer. I noticed
that majority of the students in the comparison group did not fully understand the problems and
did not use the right strategy nor earn full credits (above 50% of credits) on the problem. As a
result, the did not earn full or partial credits.
Table 19 below shows the percentage of students who correctly or partially solved the
different problem items on the rational function posttest. As indicated in the table, the students
in the treatment group clearly out performed their counterparts in the comparison group in
representations of rational functions, solving rational equations and inequalities, finding zeros
(x-intercepts), asymptotes and solving context driven problems. Students who understood these
concepts performed better on the exam as results indicate.

69
Table 19
Percentage of Students with Partial/Full Credits Scores on the RFE Items
Concept
Objective
# of
items
Item # on
RFE (see
Appendix
A)
% of students with partial
or full credit score (met
objective)
Treatment
group
Comparison
group
Rational
function
models(repre
sentations)
Students can
represent functions
in multiple ways
4
2d
8.3
6.7
3
45.8
0
4a
12.5
0
4b
12.5
13.3
Rational
equations
Students can solve
rational equations
1
1c
66.7
6.7
Rational
Inequalities
Students can solve
rational inequalities
1
1d
66.7
0
Rational
function
operations
Students can subtract
and add rational
functions
2
1a
62.5
3.3
1b
58.3
27
Domain and
range
Students can find
domain and range
1
2a
46
37
Zeros
Students can find
zeros
1
2c
71
27
Asymptotes
Students can find
asymptotes
1
2b
83.3
33.3
Context
driven
problem
Students can solve
problems in context
1
5
50
40
Total
12
Students’ Representations and Cognitive Complexity Category
According to Robinson (2001), cognitive complexity is “the processing demands of
tasks and the availability of relevant knowledge” (p.28). Five concepts of representations of
functions were put into this category (Table, written, equation, graph and multiple
representations). After five cycles of coding and recoding, two main themes emerged from this
category:
70
Theme 2: Teacher’s guidance during modeling instruction tend to help students’
mathematical representations of functions and real-world scenarios. Interview responses
from students showed that teacher guidance played a vital role in their understanding of the
concepts and motivation. Specifically, on context driven problems requiring students to
understand the problem situation and provide a route map or representation of the situation
mathematically. Student 25 from the treatment group for example, indicated during the
interview when asked to describe the aspects of the instructions that were helpful, she said
some of the real-world application problems during instruction were hard, but he did not give
up, thanks to guidance and support from the teacher. Also, when she was asked to rate her level
of satisfaction of the instruction on a scale from 1 to 5, 5 being extremely satisfied, she gave a
5. Both 2 students interviewed group stated that they were extremely satisfied with the way the
instruction was handled by the teacher. According to Mensah et al. (2013) teachers’ positive
attitudes, radiate confidence in students making them to develop positive attitude toward the
learning of mathematics.
As indicated previously, interviews were used to follow up students’ responses on the
questionnaire questions to get a better understanding of the students thinking. This was the
response of student 25 to the questionnaire question, when she was asked to describe the
aspects of the instruction that were helpful to her. She wrote:
“I learned how to find asymptotes – this was new to me. I also have more confidence finding
the x-y intercepts of an equation. Seeing the teacher work problems and explain is helpful to
me.”
The explanation from the teacher helped her understand how to find asymptotes, x, and
y-intercepts which are prerequisite concepts for graphical representations.

71
Figure 13. Response of student 25 on questionnaire question.
Here is an excerpt of my interview with student 25 on the same question she had on the
questionnaire. Speaker 1 is the interviewer (myself) and speaker 2 was the participant (student
25)
Speaker 1: Describe the aspect of the instruction that you found helpful to you.
Speaker 2: He went step by step on the board through the problems and how to graph
it.
Speaker 1: Okay.
Speaker 2: You know, didn't bounce all over and whatnot.
Speaker 1: Okay. So, what about a real-world application problem, were they helpful
to you?
Speaker 2: Yeah, he talked about oceanography and how it applies to science majors
and how you'll find it after college.
Speaker 1: Okay. And so, describe the things that you liked about the lesson.
Speaker 2: I'd have to say again, how it goes step by step through the problems.
Speaker 1: Okay.

72
Speaker 2: He gave a lot of examples.
Speaker 1: Lot of examples. And you had to work some of these problems by
yourself, on your own?
Speaker 2: Yes.
Theme 3: Mathematical modeling instruction tend to foster critical thinking and
conceptual understanding of rational functions, increasing students’ representations
capabilities and cognitive complexities. Zooming more further into the students’ solutions, an
in-depth examination of students’ artifact on the RFE pre and posttest revealed important
information and difference in conceptual understanding between the treatment and the
comparison groups. To check for conceptual understanding of the concepts, I examine the
solutions of two students (Student5 from the treatment group and student 6 from the
comparison group) on item 2d which involved representing an equation of a rational function in
graphical format. The solution of student # 5 in the treatment group who score 29% in the
pretest on RFE, scored a 73% on the posttest after the intervention showed that the student was
had good knowledge of the concepts and was well prepared for the exam than the fellow
student #6 in the comparison group. Students were not allowed to use their real names for
confidentiality and privacy purposes. They were given identification numbers (pseudonyms)
which was used throughout the study.
Presented below, are some of the misconceptions and misunderstanding in the steps
taken by two students (student 5 from treatment group and student 6 from the comparison
group) to solve problem item 2d involving representations on the RFE. Item 2d required
students to give a graphical representation of the rational function equation
)5)(2)(1(
)3)(2(
)(
−+−
+−
=
xxx
xx
xf
by hand without a graphing aid.

73
The steps to solve this problem involves knowledge of the following concepts: 1) Domain and
range item 2a, 2) intercepts (x and y) in item 2c, 3) asymptotes (horizontal, vertical and
oblique) in item 2b & 4) end behavior.
1) The domain of this function is
and Range is
2) The x-intercept is where the function intersects with the x axis found by setting y to 0
and solving for x. The y-intercept is where the function intersects with the y-axis found
by setting x to 0. The x-intercept or zeros are at x= 2 and x= -3 which are the points
(2, 0) and (-3, 0). The y intercept is f(0) = -6/10 =-3/5
3) The vertical asymptotes are the lines x= 1, x = -2 and x= 5 where the function is
undefined in the domain. The horizontal asymptotes are found by looking at the limit of
the function as x goes to infinity. If the degree of the numerator is smaller than that of
the denominator, the line y =0 is the horizontal asymptotes. That is the case with this
function.
4) End behavior involves looking at the behavior of x as y goes to infinity and the behavior
of y as x goes to infinity.
5) The resulting graph of f(x) above should look like what we have below
Figure 14. Graph of f(x) in RFE item 2d.

74
Table 20 below compares how well the two students solved item 2d.
Table 20
Comparison of Misconceptions between Student 5 and Student 6 on Item 2d of RFE
Concept Knowledge
Student 5 of treatment
group
Student 6 of comparison
group
1. Domain and range of
function f(x)
Stated domain correctly,
earned all 5 points
Stated domain correctly
Did not give the range.
Earned 2.5/5 partial credit
2. intercepts (x and y)
Found the intercepts (x
and y) and earned all 5
points
Found only the x-intercept
and earned 2.5/5
3. Asymptotes Horizontal
and vertical
Found both asymptotes
and earned all 5 points
Found both asymptotes and
earned all 5 points
4. End behavior
Showed some
knowledge on graph
No knowledge shown on
graph
5. Graphing the function f(x)
Had some knowledge of
graphing f(x) and
earned partial credits
2/5
Had no knowledge of
graphing f(x) and earned no
credits
Table 20 shows that student 5 from the treatment group had a more conceptual
understanding of rational functions than the counterpart in the comparison group and could
easily represent this rational function equation in graphical format (See appendix G).
A further examination of modeling principles as applied by the two students on problem
solving again showed a better understanding of the concepts by the student in the treatment
group compared to the other in the comparison group. Blum (2011) presents modeling principles
in the form of a modeling cycle framework which are the seven stages of the modeling process
employed to resolve a problem situation by translating from the real-world situation to
mathematics and back. These steps are 1) understanding the situation, 2) simplifying, 3)
mathematizing, 4) working mathematically, 5) interpreting the results, 6) validating the results &
7) exposing the results. Table 21 below shows how well the two students (5 and 6) above in the

75
treatment and comparison groups applied modeling principles as they solved problems on the
RFE.
Table 21
Comparison of Problem-Solving behavior of Student #5 and Student #6 on RFE
Note. Y indicate the use of modeling principle, N indicate the absence of modeling.
Student applied Modeling
principles
Item #
on RFE
Student #5 in
Treatment group
Student #6 in
comparison group
Understanding the situation,
2d
Y
N
Simplifying the situation
Y
N
Mathematizing
Y
N
Working mathematically
Y
N
Interpreting the results
Y
N
Validating the results
Y
N
Exposing the results
Y
N
Understanding the situation,
3
Y
N
Simplifying the situation
Y
N
Mathematizing
Y
N
Working mathematically
Y
N
Interpreting the results
Y
N
Validating the results
Y
N
Exposing the results
Y
N
Understanding the situation,
4a
Y
N
Simplifying the situation
Y
N
Mathematizing
Y
N
Working mathematically
Y
N
Interpreting the results
Y
N
Validating the results
Y
N
Exposing the results
Y
N
Understanding the situation,
4b
Y
Y
Simplifying the situation
Y
Y
Mathematizing
Y
Y
Working mathematically
Y
N
Interpreting the results
Y
Y
Validating the results
Y
N
Exposing the results
Y
Y

76
Table 21 suggests that application of modeling principles to problem solving enabled the
students in the treatment group to better understand the concepts, understand the problem
situation and apply the right strategy to solve the problems including representations. The student
in the comparison group on the other hand lacked understanding of the concepts and struggled
with representation of functions. This further suggests that modeling instruction could help with
students’ representations of functions.
Summary of Results
Table 22
Summary of Results
Quantitative Findings
Themes emerged
Research
question
1
Result
Research question 2 results
H
0
1
There is statistically significant
difference in Precalculus students’
average performance in a Rational
Function Exam (RFE) between
Precalculus students who receive
instruction through mathematical
modeling (M = 45.54, SD = 16.14) and
Precalculus students who receive
instruction through the traditional
lecturing approach (M = 21.21, SD =
11.71)
1. Students tend to positive views
of rational functions and
display engaging and
immersed attitudes towards
learning mathematics in a
modeling instructional setting.
H
0
2
There is a statistically significant
difference in Precalculus students’
average attitude score on an ATMI
survey between those who received
instruction through mathematical
modeling (M = 129.62, SD =12.40) and
those who receive instruction through
the traditional lecturing (M =120.54,
SD = 12.00). This test results were
consistent with the data collected.
2. Teacher’s guidance during
modeling instruction tend to
help students’ mathematical
representations of functions and
real-world scenarios.
3. Mathematical modeling
instruction tend to foster critical
thinking and conceptual
understanding of rational
functions, increasing students’
representations capabilities and
cognitive complexities
77
CHAPTER 5
Discussion and Recommendations
This section highlights the major findings for the study and situate them within the
literature. The implications and recommendations for future research are discussed as well as the
interpretation of the research findings within the scope the Blum (2011) modeling framework. A
sample of 54 Precalculus students from a local college in the southern United States took part in
this study. This exploratory embedded single case study employed both quantitative and
qualitative techniques to investigate the effects of mathematical modeling instruction on
Precalculus students’ performance and attitude toward rational functions. Two research
questions guided the investigation:
1. What is the effect of mathematical modeling instruction on Precalculus students’
performance as measured by a score on a Rational Function Exam (RFE) and
attitudes toward rational functions?
2. What is the nature of the effect of mathematical modeling instruction on the types
and cognitive complexity of representations used by Precalculus students on rational
functions?
Major Findings
Quantitatively, the analysis of the RFE results to provide answers to the first research
question indicate that students in the treatment group who were taught rational functions
through mathematical modeling instruction performed better on the RFE posttest with a mean
score of 45.54 and standard deviation of 16.14, compared to their counterparts in the
comparison group with a mean score of 21.21 and standard deviation of 11.71. This resulted in
a mean posttest score difference between the two groups of 24.33 in favor of the treatment
78
group. This suggests that mathematical modeling instruction played an important role in the
students’ mastery of rational function concepts such as multiple representations of rational
functions, solving rational function equations and inequalities, finding asymptotes of rational
functions, finding zeros, carrying out arithmetic operations with rational functions (addition,
subtraction, multiplication and division) and resolving real world problems involving rational
functions.
Similar quantitative analysis of the ATMI survey results showed that the students in the
treatment group who studied rational functions through mathematical modeling scored higher
on the ATMI posttest survey with a mean score of 129.67 compared to their counterparts in the
comparison group with a mean score of 120.54. This resulted in a mean posttest score
difference between the two groups of 9.13 in favor of the treatment group. This again suggests
that after the students were taught rational functions through mathematical modeling
instruction, they had a more favorable view of rational functions and mathematics than they did
prior to the intervention.
Qualitatively, three important themes emerged from the analysis of the artifacts,
interviews, the questionnaire and the research memos, that describing the effects of modeling
instruction on students’ types and cognitive complexity of representations of rational functions:
1. Students tend to have positive views and display engaging and immersed attitudes
towards learning mathematics in a modeling instructional setting.
2. Teacher’s guidance during modeling instruction tend to help students’ mathematical
representations of functions and real-world scenarios.

79
3. Mathematical modeling instruction tend to foster critical thinking and conceptual
understanding of rational functions, increasing students’ representations capabilities
and cognitive complexities.
Situating of Findings within the Literature
The first major finding of this study came from the quantitative data analysis which
indicated that mathematical modeling instruction impacted precalculus students’ achievement
and their attitudes towards learning of rational functions and mathematics in general. Results of
the data analysis showed that there was a statistically significant difference between the mean
posttest scores precalculus students who received instruction on rational functions through
mathematical modeling and the mean posttest score of their counterparts who were in the
traditional lecturing environment. Results also indicated a statistically significant difference
between Precalculus students’ attitudes towards rational functions in the modeling instructional
classroom and in the traditional lecturing classroom.
A review of the literature on impacts of mathematical modeling instruction on students’
attitudes and achievement (Blum, 2011; Dasher & Shahbari, 2015; Kertil & Gurel, 2016;
Mubeen et al., 2013; Mensah et al., 2013; Nourallah & Farzad, 2012; Prasad et al., 2014; Pawl et
al., 2009; Papageorgiou, 2009; Saha, 2014; Santos et al., 2015; Wedelin & Adawi, 2014 etc.),
shows similar results to those of this study. In some cases, the studies show mathematical
modeling instruction as having positive impacts on students’ mathematics achievement and in
other cases they show students display positive attitudes towards mathematics under
mathematical modeling instructional environment.
Santos et al., (2015) found that mathematical modeling instruction helps reduce students’
mathematical anxiety and had positive effects on students’ mathematics performance.

80
According to Wethall (2011), students were aware of the positive impacts of mathematical
modeling on their learning and they are more willing and able to try new problems and take
risks. Blum (2011) pointed out that modeling instruction has the potential of helping students
understand world around them, motivating them, changing their attitudes towards mathematics
and giving helping them to develop their mathematical competencies. Nourallah and Farzad
(2012) also show that university level students display problem-solving capabilities through
mathematical modeling. Sokolowski (2015) study results showed that modeling helps students
with the understanding and application mathematics. Jackson, Dukerich and Hestenes (2008)
pointed out that modeling instruction produces students who engage intelligently in public
discourse and debate about scientific and technical matters. Furthermore, studies (Mubeen et al.
2013; Prasad et al., 2014; Mensah et al., 2013; Pawl et al., 2009; Popham, 2005) indicate that
students who are taught mathematics through mathematical modeling tend to have positive
attitudes towards mathematics, hence positive outcomes on students’ mathematical achievement.
Vorhölter et al. (2014) highlighted the fact that mathematical modeling provides the
students more than just passing the examinations by showing them how mathematics is applied
in their daily lives. A similar study by Dasher and Shahbari (2015) students learn mathematics in
a meaningful way when engaged in mathematical modeling. Papageorgiou (2009) found that
students have positive views of the modeling process and are pleased that such activities are
connected to real life issues. Ellington (2005) showed that modeling-based instruction has a
positive effect on students. Niss (2012) highlighted the fact that mathematical models and
modeling are always needed either implicitly or explicitly whenever mathematics is applied to
issues, problems, situations, and contexts in domains outside of mathematics. Czocher (2017)
81
pointed out that emphasizing mathematical modeling principles in traditionally taught
differential equations course had a statistically significant effect on students’ learning.
Doerr et al. (2014) found that modeling -based mathematics instruction had a positive
impact on the students’ conception of the average rate of change and their first semester grade in
the mathematics course. Bahmaei (2013) indicated that mathematical modeling instruction has
greater effect on students’ problem-solving abilities compared to that of students in the
traditional classroom environment.
Wedelin and Adawi (2014) show that a good number of students who take
mathematical modeling courses show impressive changes in their ability to think
mathematically and they also express satisfaction with the mathematical modeling course,
noting that mathematical modeling is an important course in education. Akgün (2015) indicated
teachers’ approval of mathematical modeling citing their ability to connect to real-life and
wanting to implement the teaching method in their future classes.
I argue that mathematical modeling instruction has the potential of keeping students stay
engaged and motivated in learning of mathematics, leading to higher mathematics achievement
as the results of this study indicate. Students and teachers a like who have challenges when
dealing with rational functions and mathematics as studies indicate functions (Cangelosi et al.,
2013; Nair, 2010; Datson, 2009 etc.), can benefit from the findings of this study. With a strong
support for mathematical modeling as an instructional method gaining worldwide attention as
evident by the participation of about 30 countries around the world including the top
mathematics achieving countries including Singapore, China, Japan, Australia and Germany at
the 2009 14
th
International Conference on the Teaching of Mathematical Modeling and
Applications (ICTMA-14) in Germany (Kaiser, Blum, Ferri, & Stillman, 2011), I have no doubts
82
that mathematical modeling will continue to have lasting impacts on students’ mathematical
knowledge.
Given the fact that mathematics education currently emphasizes engaging students in
mathematical modeling instruction to understand problems of everyday life and society (Sharma,
2013; Lesh & Zawojewski, 2007; Vorhölter, Kaiser & Borromeo Ferri, 2014), I am optimistic
that through awareness and research findings as this study indicate, teachers can get the
necessary training and resources to be able to implement mathematical modeling instructional
strategies in in their classrooms. I do believe that if rational functions are considered as
mathematical models of real-life situations, which students can relate to, students may be
motivated to learn and understand mathematical concepts.
The literature also supports emerging themes from the qualitative analysis in this study.
On the first theme which indicates that students tend to have positive views and display engaging
and immersed attitudes towards learning mathematics in a modeling instructional setting,
research studies (Prasad et al., 2014; Mensah et al., 2013) have pointed to a similar conclusion.
Popham (2005) indicate that students who are taught mathematics through mathematical
modeling tend to have positive attitudes towards mathematics, hence positive outcomes on
students’ mathematical understanding and achievement. This means, that engaging students in a
mathematics classroom has the potential of producing desirable outcomes in students’ perception
of mathematics and help them to better understanding of mathematical concepts such as rational
functions. According to Saha (2014), to educate students, more emphasis should be placed on
developing positive attitude and analytic thinking skills in solving mathematical problems.
Mensah et al. (2013) indicate that teachers’ positive attitudes, radiate confidence in students
making them to develop positive attitude toward the learning of mathematics.

83
The second theme which is the idea that teacher guidance during the modeling process is
supported by the literature and is not new. Teacher play a vital role in the modeling process.
Some mathematical modeling activities can be challenging especially real-world context
problems. As such students rely times on the guidance from the teacher to solve the problem for
them, but to give more clarity to the problem. Kirschner, Sweller and Clark (2006) argued
against minimal guidance during instruction, indicating that the advantage of guidance during
instruction begins to diminish only when the learner has sufficiently prior knowledge to provide
what they called “internal” guidance. Wethall (2011) indicated that transfer among mathematical
concepts, new problems and contextual situations can occur, but requires guidance from the
instructor to become a flexible process. Blum (2011) indicated that the role of teachers
irreplaceable, suggesting some principles for teachers of mathematical modeling. He suggested
that teachers should find a permanent balance between students’ independence and their
guidance through flexibility and adaptive interventions and that teachers should support students’
individual modeling routes and encourage multiple solutions. He also called on teachers to foster
enough student strategies for solving modeling tasks and stimulate different meta-cognitive
activities like reflection on solution processes and on similarities between different situations and
contexts.
Finally, the third theme which deals with the idea that mathematical modeling instruction
tend to foster critical thinking and conceptual understanding of rational functions, increasing
students’ representations capabilities and cognitive complexities is supported by the literature as
well. According to Kertil and Gurel (2016), mathematical modeling is a bridge to the STEM
education. They believe that mathematical modeling applications provide students with
important local conceptual developments and meaningful learning of basic mathematical ideas in

84
real situations. Cognitive complexity deals with how well a person perceives and analyzes
things, events or information based on how sophisticated their thinking has become. How well
information is processed gets better with conceptual understanding. As such, when students have
conceptual understanding of representations it does increase their cognitive abilities to process
information thereby reinforcing the cognitive complexity of their representations.
Representations according to Seeger, Voight and Werschescio (1998) is “any kind of mental
state with a specific content, a mental reproduction of a former mental state, a picture, symbol or
sign, symbolic tool one has to learn their language, a something, “in place of” something else.”
These definitions of representations and cognitive complexity suggests a linear relationship
between them. Therefore, students who are better at multiple representations of functions tend to
demonstrate a high level of cognitive complexity in their representations of functions.
Recommendations for Future Research
The research findings and discussion of this study are specific to this case study on
Precalculus students at this one institution of learning in Southern United States with a limited
sample size of 54 students. The limited sample size, according to Cates (2018) contribute to the
lack of generalizability. Findings however, suggest important implications in the teaching and
learning of rational functions and mathematics and covers a significant gap in the literature. The
results may be of interest to students, teachers, mathematical curriculum developers, as well as
all those interested in mathematical modeling hoping to help improve the learning experiences of
their students.
For future research, I recommend carrying out this study with a larger sample size and in
more than one educational institution. The study was carried out on Precalculus students at this
college because rational functions were only taught in Precalculus. In some universities and
85
colleges, rational functions are taught in College Algebra. I also suggest conducting this same
study to see the effects of modeling instruction on College Algebra students.
Furthermore, this study’s quantitative findings showed that mathematical modeling had a
significant impact on students’ achievement and attitudes towards learning rational functions.
The quantitative findings were collaborated with the qualitative inquiry through multiple sources
of data including interviews, researcher’s memos, questionnaire and the attitude towards
mathematics survey. Though my visits to the teacher’s classrooms were informal, I did collect
some valuable information about the instruction in the form of memos. I am therefore suggesting
more formal observation as a source of data collection with formal observation protocols put in
place. I am also suggesting a study with a larger sample size on interviews and in different
institutions as well. Future research may also want to look at the effects of modeling on rational
functions on students with different socio- economic status and different ethnicities.
The duration for this study was five weeks. It will be interesting to find out what the
results will be for a longer period. I am therefore suggesting an entire semester (3 -4) months for
future research on mathematical modeling instruction on rational functions or related subject.
Limitations
The study had several potential limitations, which were and should be taken into considerations
with regards to the findings.
1. The fact that the different sections of the Precalculus (rational functions) were taught by
different instructors may or may not have had the teacher effect on the outcome of this
study. Different teachers provided instruction for the treatment group and the comparison
group.
86
2. The sample size was affected by subject attrition as participants eventually dropped out
for different reasons. The attrition rate for both the RFE and ATMI was 5.3% and 33.3%
for the interviews. The research findings may not be generalizable as a case study
specific to precalculus students at only one institution of learning in Southern United
States with a limited sample size of 54 students. The limited sample size, according to
Cates (2018) contribute to the lack of generalizability. The sample size for the interviews
was also small. Only four participants were interviewed.
3. Cognitive complexity is a psychological variable that can have different meanings or
definitions and hence not easy to measure or quantify.
Implications for the Future
The findings of this study have future implications in the areas of research, methodology and
practice.
The practical implications are for teaching and learning of mathematics. This study
offers teachers a researched based instructional strategy to be tried in their classrooms to
motivate and help students stay engaged and enjoy doing mathematics. Since many high school
and undergraduate teachers do not have the necessary skills and training to teach mathematical
modeling in their classes, educational institutions will therefore need to invest in professional
development to train teachers in modeling strategies so that instruction can be improved to help
students especially here in the United States where our students continue to struggle in the
STEM fields compared to other countries. According to Blum (2011), the students have a true
picture of mathematics with a better understanding of the world around them when engaged in
mathematical modeling. The students will not just be learning mathematics to pass an exam,
they will be able to understand how to apply their mathematical knowledge to their daily lives.
87
Furthermore, results of this study also show that mathematical modeling instruction
helps students with multiple ways of representations of rational functions and further reinforces
their cognitive complexity. Teachers of mathematics now can cease this opportunity to help
their students learn how to represent real life situations in multiple ways knowing that this will
help reinforce and strengthen their cognitive complexities.
In terms of research, this study bridges the gap that existed in the literature on
mathematical modeling and rational functions. The literature on modeling with other classes of
functions (linear, polynomial, exponential etc.) does exist. There is however, little or no
research out there in mathematics education on the teaching of mathematical modeling with
rational functions.
In research methodology, this study was conducted using mixed methods involving both
quantitative and qualitative techniques which future studies can replicate. The advantage of a
mixed method study is that it provides an opportunity to validate the study findings from
multiple sources of data.
Finally, this study has societal, cultural and scientific benefits as well. College and
university graduates are moving out to the society to put their knowledge into practice.
Therefore, an instructional method like modeling that prepares students for to deal with real
word situations, work collaboratively to solve problems is what our educational institutions
should pay close attention to. According to Blum (2002), the real world are things concerning
nature, society or culture, including subjects at all levels, scholarly and scientific disciplines
other than mathematics. The use of the real-world context is an essential part of teaching
mathematics for functional purposes and motivation of the students (Stacey, 2015). I am
optimizing about the future given the findings of this study. I believe that when students are
88
given the right opportunities to develop their own competencies as does in a mathematical
modeling instructional environment, students tend to have positive feelings and attitudes about
what is being taught and they tend to succeed.
Conclusion
Putting both the quantitative and qualitative findings of this study together, the results
from the quantitative and quantitative analyses of the data collected indicate that mathematical
modeling instruction had positive effects on Precalculus students’ achievement, attitudes towards
rational functions as well as the type and level of cognitive complexity of their representations of
rational functions. The students who were taught rational functions through mathematical
modeling performed better in the RFE posttest, showed positive attitudes toward mathematics
from the ATMI survey and displayed a higher ability and confidence level in their
representations than their counterparts in the traditional lecturing classroom.
Students in any classroom are there to acquire knowledge through the best means
possible to grow, to succeed and to achieve their educational and career goals. They want to be
motivated, empowered, guided as well as engaged in the learning process. It is therefore our duty
as teachers to continue to improve our skills through education, research, professional
development, and practice to provide the students the best learning experiences of their lives. As
mathematics instructors and educators in general strive for new researched based strategies of
impacting knowledge in their classrooms to ensure that their students are adequately equipped
for the job market, it is becoming obvious that some of these strategies have profound impacts on
students’ learning more than others.
This study employed both quantitative and qualitative techniques to investigate the
effects of mathematical modeling instruction on precalculus students’ performance and attitudes

89
towards rational functions. Findings from this studies and others (Blum, 2011; Nourallah &
Farzad, 2012; Mubeen et al., 2013; Prasad et al., 2014; Mensah et al., 2013; Pawl et al., 2009;
Dasher & Shahbari, 2015; Saha, 2014; Papageorgiou, 2009; Wedelin & Adawi, 2014, Jackson et
al., 2008) show that mathematical modeling instruction is certainly one of such instructional
strategies that has the potential of fostering conceptual understanding, changing students’
attitudes towards mathematics and helping them stay engaged, motivated and focused in the
learning.
This study’s findings resulting from multiple sources of data (interviews, artifacts,
research memos, questionnaire the RFE) provide some insight into the teaching and learning of
rational functions, closing the gap in the literature in the areas of mathematical modeling
instruction, rational functions, students’ achievement and students’ attitudes towards
mathematics learning. It is my wish and suggestion that future research studies be conducted on
same study with same designed with a larger sample size and in multiple institutional settings.
Finally, one of the themes from this study is that teacher-supported modeling instruction
increases students’ cognitive level and types of representations of functions. This is an important
finding in the sense that it highlights the key role that teachers play not only in a modeling
instructional environment as seen here, but also in other instructional settings in different
classrooms. This therefore suggests that teachers have and continue to hold the key to students’
success in any classroom because they determine the instructional strategy through which the
students would be best served. An engaging, supportive and empowering instructional method
from the teacher would surely leave lasting impressions on students’ learning and success.
Mensah et al. (2013) indicate that teachers’ positive attitudes, radiate confidence in students
making them to develop positive attitude toward the learning of mathematics.

90
REFERENCES
Amico, K. R. (2009). Percent total attrition: A poor metric for study rigor in hosted intervention
designs. American Journal of Public Health, 99(9), 1567-1575.
Anhalt, C. O., & Cortez, R. (2015). Mathematical modeling: A structured process. Mathematics
Teacher, 108(6), 446-452.
Anhalt, C. O., & Cortez, R. (2016). Developing understanding of mathematical modeling in
secondary teacher preparation. Journal of Mathematics Teacher Education, 19(6), 523-
545.
Akgün, L. l. (2015). Prospective mathematics teachers' opinions about mathematical modeling
method and applicability of this method. International Journal of Progressive Education,
11(2), 57-75.
Ainsworth, S. (2014). The Multiple Representation Principle in Multimedia Learning. The
Cambridge handbook of multimedia learning, 464.
Akkus, O., & Cakiroglu, E. (2010). The effects of multiple representations-based instruction on
seventh grade students’ algebra performance. CERME 6–working group 4, 420.
Aztekin, S., & Şener, Z. T. (2015). The content analysis of mathematical modelling studies in
Turkey: A meta-synthesis study. Education & Science, 40(178), 139-161.
Baxter, P., & Jack, S. (2008). Qualitative case study methodology: Study design and
implementation for novice researchers. The qualitative Report, 13(4), 544-559.
Barlow, A. T., Frick, T. M., Barker, H. L., & Phelps, A. J. (2014). Modeling instruction: The
impact of professional development on instructional practices. Science Educator, 23(1),
14.

91
Bardini, C., Pierce, R., Vincent, J., & King, D. (2014). Undergraduate mathematics students'
understanding of the concept of function. Indonesian Mathematical Society Journal on
Mathematics Education, 5(2), 85-107.
Bahmaei, F. (2013). Mathematical modelling in university, advantages and challenges. Journal
of Mathematical Modelling and Application, 1(7), 34-49.
Bal, A. P., & Doganay, A. (2014). Improving primary school prospective teachers' understanding
of the mathematics modeling process. Educational Sciences: Theory & Practice, 14(4),
1375. doi:10.12738/estp.2014.4.2042
Berry, J. S., Biehler, R., Huntley, I., Kaiser-Messmer, G., & Profke, L. (1989). Applications and
modelling in learning and teaching mathematics. W. Blum (Ed.). London: Ellis Horwood.
Besser, M., Blum, W., & Leiss, D. (2015). How to support teachers to give feedback to
modelling tasks effectively? Results from a teacher-training study in the Co2CA project.
Mathematical modelling in education research and practice (pp. 151-160). Springer
International Publishing.
Blomhøj, M. & Hoff Kjeldsen, T. (2006). Teaching mathematical modelling through project
work - Experiences from an in-service course for upper secondary teachers. ZDM, 38 (2),
163-177.
Blomhøj, M. (2008). Different perspectives on mathematical modelling in educational research-
Categorizing the TSG21 papers. In ICME 11 international Congress on Mathematics
Education (pp. 1-13).
Blomhoj, M & Kjeldsen, T. (2007). Learning the integral concept through mathematical
modelling. In: Pitta-Pantazi, D & Philippou, G. (Eds): CERME 5 – Proceedings of the

92
Fourth Congress of the European Society for Research in Mathematics Education, 2070-
2079.
Blum, W., & Niss, M. (1991). Applied mathematical problem solving, modelling, applications
and links to other subjects—State, trends and issues in mathematics instruction.
Educational Studies in Mathematics, 22(1), 37–68.
Blum, W., & Leiß, D. (2007). How do students and teachers deal with modelling problems? In
C. Haines et al. (Eds.), Mathematical modelling (ICTMA 12): Education, Engineering
and Economic (pp. 222-231). Chichester: Ellis Horwood.
Blum, W., & Kirsch, A. (1989). The problem of the graphic artist. In W. Blum, J. S. Berry,
R. Biehler, I. D. Huntley, G. Kaiser-Meßmer, & L. Profke (Eds.), Applications and
modelling in learning and teaching mathematics (pp. 129–135). Chichester: Ellis
Horwood.
Blum, W. (1993). Mathematical modelling in mathematics education and instruction. Teaching
and learning mathematics in context, 3-14.
Blum W. (2011) Can Modelling Be Taught and Learnt? Some Answers from Empirical
Research. In: Kaiser G., Blum W., Borromeo Ferri R., Stillman G. (eds). Trends in
Teaching and Learning of Mathematical Modelling. International Perspectives on the
Teaching and Learning of Mathematical Modelling,1, 15-30. New York, NY: Springer
Blum, W., & Ferri, R. B. (2009). Mathematical modelling: Can it be taught and learnt? Journal
of mathematical modelling and application, 1(1), 45-58.
Blum, W. (2015). Quality teaching of mathematical modelling: What do we know, what can we
do? In the proceedings of the 12th International Congress on Mathematical Education
(pp. 73-96). New York, NY: Springer.
93
Blum, W. (2002). ICMI Study 14: Applications and modelling in mathematics education–
Discussion document. Educational studies in mathematics, 51(1), 149-171.
Blum, W., Galbraith, P. L., Henn, H. W., & Niss, M. (2007). Modelling and applications in
mathematics education. New York, New York: Springer.
Bostic, J. D. (2011). The effects of teaching mathematics through problem-solving contexts on
sixth-grade students' problem-solving performance and representation use. (Available
from ProQuest Dissertations & Theses A&I. (1517197485). Retrieved from
http://ezproxy.gsu.edu/login?url=http://search.proquest.com.ezproxy.gsu.edu/docview/15
17197485?accountid=11226
Brenner, M. E., Mayer, R. E., Moseley, B., Brar, T., Durán, R., Reed, B. S., & Webb, D. (1997).
Learning by understanding: The role of multiple representations in learning
algebra. American Educational Research Journal, 34(4), 663-689.
Cates, M. (2018). The effects of using dragonbox on the mathematics teaching efficacy of
preservice middle grade teachers. (Doctoral Dissertation, Georgia State University).
Retrieved from https://scholarworks.gsu.edu/mse_diss/67
Czocher, J. A. (2017). How can emphasizing mathematical modeling principles benefit students
in a traditionally taught differential equations course? The Journal of Mathematical
Behavior, 45, 78-94.
Cangelosi, R., Madrid, S., Cooper, S., Olson, J., & Hartter, B. (2013). The negative sign and
exponential expressions: Unveiling students’ persistent errors and misconceptions. The
Journal of Mathematical Behavior, 32(1), 69-82.
Czocher, J. A. (2017). Mathematical modeling cycles as a task design heuristic. The Mathematics
Enthusiast, 14(1), 129-140.

94
Campbell, T., & Oh, P. S. (2015). Engaging students in modeling as an epistemic practice of
science: An introduction to the special issue of the Journal of Science Education and
Technology. Journal of Science Education and Technology, 24(2-3), 125-131.
Cope, D. G. (2014). Methods and meanings: credibility and trustworthiness of qualitative
research. In Oncology nursing forum, 41(1).
Cortina, J. M. (1993). What is coefficient alpha? An examination of theory and applications.
Journal of applied Psychology, 78(1), 98.
Cohen, D. (1995). Crossroads in mathematics: Standards for introductory college mathematics
before calculus. AMATYC, State Technical Institute in Memphis, 5983 Macon Cove,
Memphis, TN 38134. Retrieved from https://files.eric.ed.gov/fulltext/ED386231.pdf
Celik, H. C. (2017). Mathematical modelling research in Turkey: A content analysis
study. Educational Research and Reviews, 12(1), 19-27.
Crouch, R., & Haines, C. (2004). Mathematical modelling: transitions between the real world
and the mathematical model. International Journal of Mathematical Education in Science
and Technology, 35(2), 197-206.
Campbell, T., Oh, P. S., Maughn, M., Kiriazis, N., & Zuwallack, R. (2015). A review of
modeling pedagogies: Pedagogical functions, discursive acts, and technology in modeling
instruction. Eurasia Journal of Mathematics, Science & Technology Education, 11(1),
159-176.
Clearinghouse, W. W. (2014). Procedures and standards handbook (Version 3.0). Washington,
DC: US Department of Education. Retrieved from
https://ies.ed.gov/ncee/wwc/Docs/referenceresources/wwc_procedures_v3_0_standards_
handbook.pdf

95
Dedrick, R. F., Ferron, J. M., Hess, M. R., Hogarty, K. Y., Kromrey, J. D., Lang, T. R., & Lee,
R. S. (2009). Multilevel modeling: A review of methodological issues and
applications. Review of Educational Research, 79(1), 69-102.
Diekmann, O., Britton, T., & Heesterbeek, H. (2013). Mathematical Tools for Understanding
Infectious Disease Dynamics. Princeton: Princeton University Press.
Dotson, G. T. (2009). Collegiate mathematics students' misconceptions of domain and zeros of
rational functions. Retrieved from ProQuest LLC
Doerr, H. M., Ärlebäck, J. B., & Costello Staniec, A. (2014). Design and effectiveness of
modeling‐based mathematics in a summer bridge program. Journal of Engineering
Education, 103(1), 92-114.
Doruk, B. K., & Umay, A. (2011). The effects of mathematical modeling on transferring
mathematics into daily life. Hacettepe University Journal of Education, 41, 124-125.
Dundar, S., Gokkurt, B., & Soylu, Y. (2012). Mathematical modelling at a glance: a theoretical
study. Procedia-Social and Behavioral Sciences, 46, 3465-3470.
Daher, W., & Shahbari, J. (2015). Pre-service teachers’ modeling processes through engagement
with model eliciting activities with a technological tool. International Journal of Science
& Mathematics Education, 13(1), 25-46.
Dedoose (2017). Web application for managing, analyzing and presenting qualitative and mixed
method research data (Version 8.0.23). Los Angeles, CA: Socio Cultural Research
Consultants, LLC. Retrieved from www.dedoose.com
Dym, C. (2004). Principles of mathematical modeling. Academic press.
Doerr, H.M. (2006). Teachers’ ways of listening and responding to students’ emerging
mathematical models. ZDM, 38(3), .255-268.

96
Deal, J. (2015). Students’ mathematical modeling in algebra (Doctoral dissertation, University of
Illinois at Urbana-Champaign).
Erbas, A. K., Kertil, M., Çetinkaya, B., Çakiroglu, E., Alacaci, C., & Bas, S. (2014).
Mathematical modeling in mathematics education: Basic concepts and approaches.
Educational Sciences: Theory and Practice, 14(4), 1621-1627.
Fennel, F. (2006). Representation—show me the math. National Council of Teacher of
Mathematics, 1.
Frejd, P. (2013). Modes of modelling assessment-a literature review. Educational Studies in
Mathematics, 84(3), 413-438. doi:10.1007/s10649-013-9491-5
Ferri, R. B. (2006). Theoretical and empirical differentiations of phases in the modelling process.
ZDM, 38(2), 86-95.
Frejd, P., & Bergsten, C. (2016). Mathematical modelling as a professional task. Educational
Studies in Mathematics, 91(1), 11-35. doi:10.1007/s10649-015-9654-7.
Frejd, P. (2014). Modes of mathematical modelling: An analysis of how modelling is used and
interpreted in and out of school settings (Doctoral dissertation, Linköping University
Electronic Press).
Fennel, F. (2006). Representation - show me the math. National Council of Teacher of
Mathematics, 1.
Freeman, A. L. (2014). The impact of small-group mathematical modeling activities on students'
understanding of linear and quadratic functions. (Doctoral dissertation, Teachers college,
Columbia University).
Frejd, P. (2011). Mathematical modelling in upper secondary school in Sweden: An exploratory
investigation (Doctoral dissertation, Linköping University Electronic Press).

97
Gordon, S. P. (2008). What's Wrong with College Algebra? Primus, 18(6), 516-541.
Gonzales, P., Williams, T., Jocelyn, L., Roey, S., Kastberg, D., & Brenwald, S. (2008).
Highlights from TIMSS 2007: Mathematics and Science Achievement of US Fourth-and
Eighth-Grade Students in an International Context. NCES 2009-001. National Center for
Education Statistics.
Gould, H. (2013). Teachers' conceptions of mathematical modeling. Available from ProQuest
Dissertations & Theses A&I. (1367590532). Retrieved from
http://ezproxy.gsu.edu/login?url=http://search.proquest.com.ezproxy.gsu.edu/docview/13
67590532?accountid=11226
García, F.J., Gascón, J., Ruiz Higueras, L. & Bosch, M. (2006). Mathematical modelling as a
tool for the connection of school mathematics. ZDM, 38(3), 226-246
Gellert, U., Jablonka, E. & Keitel, C. (2001). Mathematical Literacy and Common Sense in
Mathematics Education. In B. Atweh, H. Forgasz & B. Nebres (Eds.), Sociocultural
Research on Mathematics Education (pp. 57- 76). Mahwah: Lawrence Erlbaum
Associates
Galbraith, P. & Stillman, G. (2006). A framework for identifying student blockages during
transitions in the Modelling process. ZDM, 38 (2), 143-162
Greefrath, G., & Vorhölter, K. (2016). Teaching and learning mathematical modelling:
approaches and developments from German speaking countries. Teaching and learning
mathematical modelling (pp. 1-42). New York, NY: Springer.
Girnat, B., & Eichler, A. (2011). Secondary Teachers’ Beliefs on Modelling in Geometry and
Stochastics. Trends in teaching and learning of mathematical modelling (pp. 75-84). New
York, NY: Springer.

98
Groshong, K. g., & Joo Young Park2, j. (2016). Examining secondary mathematics teachers’
mathematical modeling knowledge for teaching. Conference Papers - Psychology of
Mathematics & Education of North America, 1682-1689.
Gökyürek, B. (2016). An analysis of leisure attitudes of the individuals participating in dance
activities and the relationship between leisure attitude and life satisfaction. International
Journal of Environmental and Science Education, 11(10), 3285-3296.
Hancock, D. R., & Algozzine, B. (2015). Doing case study research: A practical guide for
beginning researchers. Teachers College Press.
Haines, C., & Crouch, R. (2007). Mathematical modelling and applications: Ability and
competence frameworks. In W. Blum, P. L. Galbraith, H. Henn, & M. Niss (Eds.),
Modelling and applications in mathematics education. The 14th ICMI study (pp. 417-
424). New York, NY: Springer.
Herriott, S. R., & Dunbar, S. R. (2009). Who takes college algebra? Primus, 19(1), 74-87.
Hornsby Jr, E. J., & Cole, J. A. (1986). Rational functions: Ignored too long in the high school
curriculum. Mathematics Teacher, 79(9), 691-98.
Huson, C. J. (2016). Mathematical modeling from the teacher's perspective (Order No.
10107561). Available from ProQuest Dissertations & Theses A&I. (1791403916).
Retrieved from
http://ezproxy.gsu.edu/login?url=http://search.proquest.com.ezproxy.gsu.edu/docview/17
91403916?accountid=11226
Haines, C. R., & Crouch, R. (2013). Remarks on a modeling cycle and interpreting behaviors. In
Modeling Students' Mathematical Modeling Competencies (pp. 145-154). New York,
NY: Springer

99
Hiltrimartin, C., Hartono, Y., & Scristia, S. (2018). The Teachers Conception of Mathematical
Modelling at Palembang. Pancaran Pendidikan, 7(1).
Iversen, S.M. & Larson, C.J. (2006). Simple thinking using complex math vs. complex thinking
using simple math. ZDM, 38(3), 281-292.
Imm, K. L., & Lorber, M. D. (2013). The footprint problem: A pathway to modeling.
Mathematics teaching in the Middle school, 19(1), 46-54.
Jackson, J., Dukerich, L., & Hestenes, D. (2008). Modeling Instruction: An Effective Model for
Science Education. Science Educator, 17(1), 10-17.
Jacobs, G. g., & Durandt, R. (2017). Attitudes of pre-service mathematics teachers towards
modelling: A South African inquiry. Eurasia Journal of Mathematics, Science &
Technology Education, 13(1), 61-84. doi:10.12973/eurasia.2017.00604a
Kaiser, G., Blum, W., Ferri, R. B. & Stillman, G. (Ed.). (2011). International perspectives on the
teaching and learning of mathematical modeling. New York: Springer.
Kaiser, G., & Schwarz, B. (2006). Mathematical modelling as bridge between school and
university. ZDM, 38(2), 196-208.
Kaiser, G., Busse, A., Hoth, J., König, J., & Blömeke, S. (2015). About the complexities of
video-based assessments: Theoretical and methodological approaches to overcoming
shortcomings of research on teachers’ competence. International Journal of Science and
Mathematics Education, 13(2), 369-387.
Kaiser, G., & Sriraman, B. (2006). A global survey of international perspectives on modelling in
mathematics education. ZDM, 38(3), 302-310.
100
Kertil, M., & Gurel, C. (2016). Mathematical modeling: A bridge to STEM
Education. International Journal of Education in Mathematics, Science and
Technology, 4(1), 44-55. DOI:10.18404/ijemst.95761
Kirschner, P. A., Sweller, J., & Clark, R. E. (2006). Why minimal guidance during instruction
does not work: An analysis of the failure of constructivist, discovery, problem-based,
experiential, and inquiry-based teaching. Educational psychologist, 41(2), 75-86.
Li, Z., Zhu, C., & Gold, C. (2004). Digital terrain modeling: principles and methodology. Boca
Raton: CRC press.
León, K., García, K., & Lage, A. (2008). Mathematical modeling of the implications of dominant
tolerance for tumor biology and the response to combination therapy. Biotecnologia
Aplicada, 25(4), 396-399.
Lesh, R. & Zawojewski, J. (2007). Problem solving and modeling. In F. K. Lester (Ed.), Second
handbook of research on mathematics teaching and learning. Charlotte: Information age.
Lesh, R., English, L., Sevis, S., & Riggs, C. (2013). Modeling as a means for making powerful
ideas accessible to children at an early age. Hegedus, S. & Roschelle, J. (Eds.), The
SimCalc vision and contributions: Democratizing access to important mathematics.
Berlin: Springer.
Lesh, R., Post, T. R., & Behr, M. (1987). Representations and translations among representations
in mathematics learning and problem solving. In Problems of representations in the
teaching and learning of mathematics. Lawrence Erlbaum.
Lewis, M. S. (2013). A Series of Sensitivity Analyses Examining the What Works
Clearinghouse's Guidelines on Attrition Bias (Doctoral dissertation, Ohio University).
101
Retrieved from
https://etd.ohiolink.edu/!etd.send_file?accession=ohiou1386239081&disposition=inline
Lingefjard, H. T. (2000). Mathematical modeling by prospective teachers using
technology (Order No. 0801674). Available from ProQuest Dissertations & Theses A&I.
(304589501). Retrieved from http://ezproxy.gsu.edu/login?url
=http://search.proquest.com.ezproxy.gsu.edu/docview/304589501?accountid=1122
Lingefjärd, T. (2006). Faces of mathematical modelling. ZDM, 38 (2), 96-112.
Leong, K.E. (2012). Assessment of Mathematical Modeling. Journal of Mathematics Education
at Teachers College, 3(1):61-65. New York.
Majeed, A. A., Darmawan, I. G. N, & Lynch, P. (2013). A confirmatory factor analysis of the
attitudes toward mathematics inventory (ATMI). The Mathematics Educator, 15(1), 120
– 135.
Magnus, C., Brandenberg, O. F., Rusert, P., Trkola, A., & Regoes, R. R. (2013). Research paper:
Mathematical models: A key to understanding HIV envelope interactions? Journal of
Immunological Methods, 398-3991-18. doi: 10.1016/j.jim.2013.09.002
Maria, L. H., Rachel L., Mathew, D. F., & Rose, M. Z. (2017). Mathematical modeling in the
high school curriculum. The mathematics teacher, 110(5), 336-342.
doi:10.5951/mathteacher.110.5.0336
Nair, G. S. (2010). College students’ concept images of asymptotes, limits, and continuity of
rational functions (Doctoral dissertation, The Ohio State University).
Niss, M. (2012). Models and modelling in mathematics education. Newsletter of the European
Mathematical Society, 86, 49-52.
102
Perrenet, J., & Zwaneveld, B. (2012). The many faces of the mathematical modeling cycle.
Journal of Mathematical Modelling and Application, 1(6), 3-21.
Pelesko, J. A., Cai, J., & Rossi, L. F. (2013). Mathematical modeling: Developing habits of
mathematical minds. Educational interfaces between mathematics and industry (pp. 237-
245). New York, NY: Springer
Pollak, H. O. (1968). On some of the problems of teaching applications of mathematics.
Educational Studies in Mathematics, 1(1/2), 24–30.
Perrenet, J., & Zwaneveld, B. (2012). The many faces of the mathematical modeling cycle.
Journal of Mathematical Modelling and Application, 1(6), 3-21.
Pierce, P. & Stacey, K. (2006). Enhancing the image of mathematics by association with simple
pleasures from real world contexts. ZDM 38(3), 214-225.
Rese, A., Schreiber, S., & Baier, D. (2014). Technology acceptance modeling of augmented
reality at the point of sale: Can surveys be replaced by an analysis of online
reviews? Journal of Retailing and Consumer Services, 21(5), 869-876.
Richard, B. W., Holton, I. F., & Katsioloudes, V. (2014). The use of discrete computer
simulation modeling to estimate return on leadership development investment. The
Leadership Quarterly, 251054-1068. doi: 10.1016/j.leaqua.2014.03.002.
Robinson, N. (2016). A case study exploring the effects of using an integrative STEM curriculum
on eighth grade students’ performance and engagement in the mathematics classroom
(Doctoral Dissertation) Georgia State University. Retrieved from
http://scholarworks.gsu.edu/mse_diss/32
Robinson, P. (2001). Task complexity, task difficulty, and task production: Exploring
interactions in a componential framework. Applied linguistics, 22(1), 27-57.

103
Saxena, R., Shrivastava, K., & Bhardwaj, R. (2016). Teaching mathematical modeling in
mathematics education. Journal of Education and Practice, 7(11), 34-44.
Sabella, C. Henderson, & C. Singh (Eds.), AIP Conference Proceedings 1179(1), 51-54.
Saldaña, J. (2013). The coding manual for qualitative researchers. Sage
Saldaña, J. (2015). The coding manual for qualitative researchers. Sage
Shadish, W. R., Cook, T. D., & Campbell, D. T. (2002). [BOOK REVIEW] Experimental and
quasi-experimental designs for generalized causal inference. Social Service Review,
76(3), 510-514.
Sharma, A. (2013). Associations between self-efficacy beliefs, self-regulated learning strategies,
and students' performance on model-eliciting tasks: An examination of direct and indirect
effects. Retrieved from ProQuest LLC, 2013. ERIC, EBSCOhost
Smith, L. A. (2013). Comparing the effectiveness of reform pedagogy to traditional didactic
lecture methods in teaching remedial mathematics at four-year universities (Doctoral
dissertation, Auburn University).
Santos, M. L. K. P., Belecina, R. R., & Diaz, R. V. (2015). Mathematical modeling: effects on
problem solving performance and math anxiety of students. International Letters of
Social and Humanistic Sciences, 65, 103-115.
Sokolowski, A. (2015). The Effects of mathematical modelling on students' achievement-meta-
analysis of research. IAFOR Journal of Education, 3(1), 93-114.
Sole, M. (2013). A primer for mathematical modeling. Journal of Mathematics Education at
Teachers College, 4(2).
104
Shen, J., Lei, J., Chang, H. Y., & Namdar, B. (2014). Technology-enhanced, modeling-based
instruction (TMBI) in science education. In handbook of research on educational
communications and technology (pp. 529-540). New York: Springer.
Stacey, K. (2015). The real world and the mathematical world. In Assessing Mathematical
Literacy (pp. 57-84). Springer International Publishing.
Sriraman, B. & Lesh, R. (2006). Modeling conceptions revisited. ZDM 38(3), 247-254.
Schukajlow, S., Krug, A., & Rakoczy, K. (2015). Effects of prompting multiple solutions for
modelling problems on students’ performance. Educational Studies in Mathematics,
89(3), 393-417.
Schukajlow, S., Leiss, D., Pekrun, R., Blum, W., Müller, M., & Messner, R. (2012). Teaching
methods for modelling problems and students’ task-specific enjoyment, value, interest
and self-efficacy expectations. Educational studies in mathematics, 79(2), 215-237.
Seeger, F., & Waschescio, U. (Eds.). (1998). The culture of the mathematics classroom.
Cambridge University Press
Tapia, M., & Marsh, G. E. (2004). An instrument to measure mathematics attitudes. Academic
Exchange Quarterly, 8(2), 16-22.
Tao, C. V., & Hu, Y. (2001). A comprehensive study of the rational function model for
photogrammetric processing. Photogrammetric engineering and remote sensing, 67(12),
1347-1358.
Temur, Ö. D. (2012). Analysis of Prospective Classroom Teachers' Teaching of Mathematical
Modeling and Problem Solving. Eurasia Journal of Mathematics, Science & Technology
Education, 8(2).

105
Thrasher, E. P. (2016). An investigation of mathematical modeling with pre-service secondary
mathematics teachers (Order No. 10585459). Available from ProQuest Dissertations &
Theses A&I. (1884307268). Retrieved from
http://ezproxy.gsu.edu/login?url=http://search.proquest.com.ezproxy.gsu.edu/docview/18
84307268?accountid=11226
Tchoshanov, M., Cruz, M. D., Huereca, K., Shakirova, K., Shakirova, L., & Ibragimova, E. N.
(2015). Examination of lower secondary mathematics teachers’ content knowledge and
its connection to students’ performance. International Journal of Science and
Mathematics Education, 1-20.
Törner, G., Potari, D., & Zachariades, T. (2014). Calculus in European classrooms: curriculum
and teaching in different educational and cultural contexts. ZDM, 46(4), 549-560.
U.S. Department of Education, Institute of Education Sciences, National Center for Education
Statistics, National Assessment of Educational Progress (NAEP), 2017 Mathematics
Assessment.
Vos, P. (2011). What Is ‘Authentic’ in the Teaching and Learning of Mathematical Modelling?
In Trends in teaching and learning of mathematical modelling (pp. 713-722). Springer
Netherlands.
Vorhölter K., Kaiser G., Ferri R. B. (2014). Modelling in mathematics classroom instruction: an
innovative approach for transforming mathematics education. In: Li Y., Silver E., Li S.
(Eds.), Advances in mathematics education. Transforming Mathematics Instruction.
Multiple approaches and practices (pp. 21–36). Cham: Springer.
Weber, V., Fortune, N., Williams, D., & Whitehead, A. (2016). Mathematical modeling with My
Maps and Spreadsheets. Mathematics Teacher, 110(2), 147-150.

106
Wedelin, D., & Adawi, T. (2014). Teaching mathematical modelling and problem solving-A
Cognitive Apprenticeship Approach to Mathematics and Engineering
Education. JEP, 4(5), 49.
Wolf, N. B. (2013). Teachers' understanding of and concerns about mathematical modeling in
the common core standards (Order No. 3590815). Available from ProQuest Dissertations
& Theses A&I. (1432193702). Retrieved from http://ezproxy.gsu.edu/login?url=
http://search.proquest.com.ezproxy.gsu.edu/docview/1432193702?accountid=11226
West, J. G. (2013). Comparing the impact of traditional and modeling college algebra courses
on student performance in survey of calculus (Doctoral Dissertation ) University of
Arkansas Retrieved from
http://ezproxy.gsu.edu/login?url=http://search.proquest.com.ezproxy.gsu.edu/docview/13
18500819?accountid=11226.
Wethall, N. (2011). The Impact of Mathematical Modeling on Student Learning and Attitudes
(Doctoral dissertation, master’s thesis, The Evergreen State College). Retrieved from
http://archives. evergreen. edu/masterstheses/Accession2010-
03MEd/2011/Wethall_Nicola_MEd_2011. pdf)
Wilkins, J. L., & Ma, X. (2003). Modeling change in student attitude toward and beliefs about
mathematics. The Journal of Educational Research, 97(1), 52-63.
Wijaya, A. (2015). Context-based mathematics tasks in Indonesia: Toward better practice and
achievement. Utrecht University.
Wells, M., Hestenes, D., & Swackhamer, G. (1995). A modeling method for high school physics
instruction. American Journal of Physics, 63(7), 606-619.
107
Yin R. K. (2004). Case study methods in COSMOS Corporation. Complementary methods for
research in Education of American Research Association, Washington DC.
Yin, R. K. (2013). Case study research: Design and methods. Sage publications.
Yin, R. K. (2009). Case study research: Design and methods (4th Ed.). Thousand Oaks, CA:
Sage
Yee, N. K., & Lam, T. T. (2008). Pre-university students' errors in integration of rational
functions and implications for classroom teaching. Journal of Science and Mathematics
Education in Southeast Asia, 31(2), 100-116.
Yin, R. K. (2014). Case Study Research Design and Methods (5th ed.). Thousand Oaks, CA:
Sage.
Yilmaz, S., & Dede, A. T. (2016). Mathematization competencies of pre-service elementary
mathematics teachers in the mathematical modelling process. International Journal of
Education in Mathematics, Science and Technology, 4(4), 284-298.
Zbiek, R. M., & Conner, A. (2006). Beyond motivation: Exploring mathematical modeling as a
context for deepening students' understandings of curricular mathematics. Educational
Studies in Mathematics, 63(1), 89-112.

108
APPENDICES
Appendix A
Pre/posttest - Rational Function Exam (RFE)
Participant Identification Code_________________________________________________
Date: _________________________________________________
Time 40 minutes Show all your work.
_____________________________________________________________________________
1. Given the rational functions
f(x) = and g(x) =
, find and simplify your solution
a) f(x) - g(x)
b)
c) Solve the rational equation f(x) = g(x)
d) Solve the rational inequality f(x) < 0

109
2. Given the function
)5)(2)(1(
)3)(2(
)(
−+−
+−
=
xxx
xx
xf
a) What is the domain and range of the function f(x)
b) Find the vertical, horizontal and oblique asymptotes for the function f(x) if any.
c) Find the x and y intercepts of the function f(x)
110
d) Sketch the graph of the function f(x) without using technology
3. Write an equation for the rational function with the following characteristics:
Vertical asymptotes at
5x =
and
5x =−
, x intercepts at
(2, 0)
and
( 1, 0)−
, y intercept at
( )
0, 4

111
4. Given this graph of a rational function f
a) Write the equation of the function
b) Describe the end behavior of the function f in words
5. A rare species of insect was discovered in the rain forest of Costa Rica.
Environmentalists transplant the insect into a protected area. The population of the insect
t months after being transplanted is
a. What was the population when t = 0?
b. What will the population be after 10 years?
c. When will there be 549 insects?

112
Appendix B
Attitude Toward Mathematics Inventory adopted from Tapia and Marsh (2004)
Directions: This inventory consists of statements about your attitudes toward mathematics. There
are no correct or incorrect responses. Read each item carefully and think about how you feel
about each item. Indicate the number that most closely corresponds to how each statement best
describes your feelings. Please answer every question.
PLEASE USE THESE RESPONSE CODES:
1 = Strongly Disagree
2 = Disagree
3 = Neutral
4 = Agree
5 = Strongly Agree
No
Statement
1 2 3 4 5
1
Mathematics is a very worthwhile and necessary subject.
2.
I want to develop my mathematical skills.
3.
I get a great deal of satisfaction out of solving a mathematics problem
involving rational functions.
4.
Mathematics helps develop the mind and teaches a person to think.
5.
Mathematics is important in everyday life.
6.
Mathematics is one of the most important subjects for people to study.
7.
High school courses would be very helpful no matter what I decide to
study.
8.
I can think of many ways that I use math outside of school
9.
Mathematics is one of my dreaded subjects.
10.
My mind goes black and I am unable to think clearly when working
with mathematics.
11.
Studying mathematics makes me feel nervous.
12.
Mathematics makes me feel uncomfortable.
13.
I am always under a terrible strain in a math class.
14.
When I hear the word mathematics, I have the feeling of dislike.
15.
It makes me nervous to even think about having to do a mathematics
problem.
16.
Mathematics does not scare me at all
17.
I have a lot of self-confidence when it comes to mathematics
18.
I am able to solve a mathematics problem without too much difficulty.
19.
I expect to do fairly well in any math class I take.
20.
I am always confused in my mathematics class.
21.
I feel a sense of insecurity when attempting mathematics.

113
22.
I learn mathematics easily.
23.
I am confident that I could learn advanced mathematics.
24.
I have usually enjoyed studying mathematics in school.
25.
Mathematics is dull and boring.
26.
I like to solve new problems in mathematics.
27.
I would prefer to do an assignment in math than to write an essay.
28.
I would like to avoid using mathematics in college.
29.
I really like mathematics.
30.
I am happier in a math class than in any other class.
31.
Mathematics is a very interesting subject.
32.
I am willing to take more than the required amount of mathematics.
33.
I plan to take as much mathematics as I can during my education.
34.
The challenge of math appeals to me.
35.
I think studying advanced mathematics is useful.
36.
I believe studying math helps me with problem solving in other areas.
37.
I am comfortable expressing my own ideas on how to look for
solutions to a difficult problem in math.
38.
I am comfortable answering questions in math class
39.
A strong math background could help me in my professional life.
40.
I believe I am good at solving math problems.
© 1996 Martha Tapia
114
Appendix C
Research Questionnaire
Thanks for providing your candid responses to the following questionnaire. There are 6
questions intended to learn about your experience with the way you have just learned rational
functions.
1. What is your ethnicity and gender?
Ethnicity: ___________________________________ Gender____________________
2. What is your major and first language?
Major: _____________________________________ First language________________
3. Have you been taught rational functions before this study? If so, where, when and how
was your experience with rational functions then?
4. How do you feel about rational functions now after the lessons you just received?
5. Describe one aspect of the instruction that you find helpful to you.
6. Describe any barriers (if any) that you encountered during this study session
115
7. On a scale of 1 to 5 rate your level of satisfaction with the way you were taught rational
functions, 1 being the least satisfied and 5 being extremely satisfied.
8. Would you recommend a friend or someone to a school that teaches rational functions the
way you have been taught? Yes/No. Please explain your answer.
9. Is there anything you would like to say or add?
Thank you for your time.
116
Appendix D: Interview Protocols
I want to thank you for taking the time to meet with me today for this interview. My name is
Solomon Betanga and the purpose of this short semi structured interview is to understand about
your learning experience during this 5-weeks study of rational functions. This information will
be used in my dissertation study. I will be audio recording this interview and the transcripts will
be submitted to you for your review before I use it in my study. Please answer in as more details
as you like. This interview should take approximately 20 to 25 minutes.
Please be aware that all your responses will be kept confidential and will only be used for this
study. Also, note that you are not obliged to say anything you do not want to, and you may end
the interview at any time.
Questions
1. Have you had a lesson on rational functions before this study? If yes, where and when?
2. Describe aspects of the instruction that you found helpful to you.
3. Describe aspects if any of the instruction that you did not like
4. Describe the things you liked about the way the lessons on rational functions were
presented to you.
5. Describe any barriers of difficulties (if any) that you encountered during this study
session.
6. Would you say that you have more understanding of rational functions now than before?
If yes or no, explain you answer.
7. Are you more confident of yourself now to handle rational function problems? If yes or
no, explain.
117
8. On a scale of 1 to 5 rate your level of satisfaction with the way you were taught rational
functions, 1 being the least satisfied and 5 being extremely satisfied.
9. Would you recommend a friend or someone to a school that teaches rational functions the
way you were taught? Yes/No. Please explain your answer.
10. Is there anything you would like to say or add?
Thank you for your time.

118
Appendix E
Informed Consent for Students Participants
Title: A Research Study on the Effects of Mathematical Modeling on Precalculus Students’
Performance and Attitudes towards Rational Functions.
Principal Investigator: Dr. Iman Chahine
Student Principal Investigator: Solomon Betanga
Purpose:
The purpose of this research study is to find out if there is a significant difference between the
performance of Precalculus students who are taught rational functions through mathematical
modeling and those who are taught rational functions through the traditional lecturing method.
You are invited to take part in the study because you are Precalculus students this semester. A
total of 60 people will be invited to take part in this research study.
Procedure:
If you decide to take part in this research study, you will complete the following assessments
administered by the researcher and the data will be used for this study.
- A pretest and a posttest on Rational Functions.
- A pretest and a posttest on an attitude towards mathematics survey.
- A questionnaire on your thoughts about the instructional method used to teach you
rational functions.
Future Research:
Researchers will not use or distribute your data for future research study.
Risks:
In this research study, will not have any more risks than you would in a normal day of life.
Benefits:

119
This research study is not designed to benefit you personally. Overall, we hope to gain
information about the teaching and learning of rational functions.
Alternatives:
If you decide not to take part in this research study, you will be given different problems not related
to this research study to work on during this class time.
Voluntary Participation and Withdrawal:
You do not have to be in this research study. If you decide to be part and change your mind, you
have the right to drop out at any time. You may skip questions or stop participating at any time.
Confidentiality:
We will keep your records private to the extent allowed by the law. The following people and
entities will have access to the information you provide:
• Primary investigator (P.I.) Dr. Iman Chahine and the student P.I. Solomon Betanga.
• GSU Institutional Review Board.
• Office of Human Research Protection (OHRP).
We will use pseudonyms rather than your name on the records. The information you provide will
be stored. When we present or publish the results, we will not use your name or other
information that may identify you.
Contact Persons:
Contact the Primary Investigator Dr. Iman Chahine at [email protected] and the student primary
investigator Solomon Betanga at [email protected],
• If you have questions about the research study or your part in it

120
• If you have questions, concerns, or complaints about the research study
Contact the GSU Office of Human Research Protection at 404-413-3500 or [email protected]
• If you have questions as a research participant
• If you have questions, concerns, or complaints about the research study
Consent:
You will get a copy of the consent to keep.
If you are willing to volunteer for this study, please sign below:
__________________________________________
Name of participant
___________________________________________ ___________________
Signature of participants Date
___________________________________________ _____________________
Researcher obtaining consent Date
121
Appendix F
Recruitment Script to be Read to the Students
Hello students, my name is Solomon Betanga. I am a lecturer of mathematics here at
Gordon State College. I am conducting a research study to find out if there is a significant
difference between the performance of Precalculus students who are taught rational functions
through mathematical modeling and those who are taught rational functions through the traditional
lecturing method. You are invited to take part in the study because you are Precalculus students.
If you decide to take part in the study, you will complete the following assessments
administered by the researcher and the data will be used for this study.
- A pretest and a posttest on Rational Functions.
- A pretest and a posttest on an attitude towards mathematics survey.
- A questionnaire on your thoughts about the instructional method used to teach you
rational functions.
If you decide not to take part in this research study, you will be given different problems not related
to this research study to work on during this class time.
Participation in this study is strictly voluntary and your identity will remain confidential during
and after the study since you will not be using your real names on any assessment.
If you have any questions and would like to participate in the study, you can ask me when I give
you the consent form to indicate whether you want to be part of the research study.
Thank you for your participation.

122
Appendix G
Artifacts of Students’ Work
Artifact of Student 1 from treatment group
Artifact of Student 24 from treatment group

123
Artifact of Student 5 from treatment group
Artifact of Student 6 from treatment group Researchers’ memo
