
Financial M athem atics
fo r Act u a r ie s
Chapter 2
Ann uities

Learning Objectives
1. Annuit y-immediate and annuity-due
2. Present and future values of annuities
3. Perpetuities and deferred annuities
4. Other accumulation m ethods
5. Payment periods and com pounding periods
6. Varying annuities
2

2.1 A nn uit y-Im mediate
• Consider an annuit y with payments of 1 unit eac h, made at the end
of ev ery year for n years.
• T his kind of annuit y is called an annuit y-imm ediate (also called
an ordinary annuit y or an annuit y in arrears).
• The present value of an ann uit y is the sum of the present values
of eac h payment.
Example 2.1: Calculate the presen t value of an ann uity-imm ediate of
amount $100 paid ann ually for 5 years at the rate of in terest of 9%.
Solution: Table 2.1 summ arizes the presen t values of the payments as
well as their total.
3

Table 2.1: Presen t value of ann uity
Year Payment ($) Present value ($)
1100100 (1.09)
−1
=91.74
2100100 (1.09)
−2
=84.17
3100100 (1.09)
−3
=77.22
4100100 (1.09)
−4
=70.84
5100100 (1.09)
−5
=64.99
Total 388.97
2
• Weareinterestedinthevalueoftheannuityattime0,calledthe
present value, and the accumulated value of the ann uity at time n,
called the future value.
4

• Suppose the rate of in terest per period is i,andweassumethe
compound-in terest method applies.
• Let a
n
e
i
denote the present value of the ann uit y, whic h is sometim es
denoted as a
n
e
when the rate of in terest is understood.
• As the presen t value of the jth payment is v
j
,wherev =1/(1 + i) is
the discoun t factor, the present value of the annuity is (see Appendix
A.5 for the sum of a geometric progression)
a
n
e
= v + v
2
+ v
3
+ ···+ v
n
= v ×
∙
1 − v
n
1 − v
¸
=
1 − v
n
i
=
1 − (1 + i)
−n
i
. (2.1 )
5


• The accumulated value of the ann uit y at time n is denoted b y s
n
e
i
or s
n
e
.
• This is the future value of a
n
e
at time n.Thus,wehave
s
n
e
= a
n
e
× (1 + i)
n
=
(1 + i)
n
− 1
i
. (2.2 )
• If the ann uit y is of lev el payments of P, the present and future values
of the annuity are Pa
n
e
and Ps
n
e
, respectively.
Example 2.2: Calculate the presen t value of an ann uity-imm ediate of
am ount $100 paid annually for 5 y ears at the rate of in terest of 9% using
formula (2.1). Also calculate its future value at time 5.
6

Solution: From (2.1), the present value of the annuity is
100 a
5
e
=100×
"
1 − (1.09)
−5
0.09
#
=$388.97,
whic h agrees with the solution of Example 2.1. The future value of the
annuity is
(1.09)
5
× (100 a
5
e
)=(1.09)
5
× 388.97 = $598.47.
Alternativ ely, the future value can be calculated as
100 s
5
e
=100×
"
(1.09)
5
− 1
0.09
#
=$598.47.
2
Example 2.3: Calculate the presen t value of an ann uity-imm ediate of
amount $100 pa yable quarterly for 10 years at the annual rate of interest
7

of 8% convertible quarterly. A lso calculate its future value at the end of
10 years.
Solution: Note that the rate of in terest per pa ym ent period (quarter)
is (8/4)% = 2%,andthereare4 × 10 = 40 pa ym ents. Thus, from (2.1)
thepresentvalueoftheannuity-immediateis
100 a
40
e
0.02
=100×
"
1 − (1.02)
−40
0.02
#
=$2,735.55,
an d th e fut ure va lue of th e annuity-imme dia t e is
2735.55 × (1.02)
40
=$6,040.20.
2
• A common problem in financial m anagement is to determine the in-
stallm ents required to pay bac k a loan. We may use (2.1) to calculate
the amo unt of level installm ents required.
8

Example 2.4: A man borro w s a loan of $20,000 to purchase a car at
annual rate of interest of 6%. He will pay bac k the loan through m onthly
installments o ver 5 years, w ith the first insta llm ent to be m ad e one mo nth
after the release of the loan. What is the monthly installment he needs to
pa y?
Solution: The rate of interest per pa ym ent period is (6/12)% = 0.5%.
Let P be the monthly installm ent. As there are 5 × 12 = 60 pa ym ents,
from (2.1 ) we have
20,000 = Pa
60
e
0.005
= P ×
"
1 − (1.005)
−60
0.005
#
= P × 51.7256,
9

so that
P =
20,000
51.7256
=$386.66.
2
• The exam ple belo w illustrates the calculation of the required install-
ment for a targeted future value.
Example 2.5: A man wan ts to sav e $100,000 to pay for his son’s
education in 10 years’ time. An education fund requires the in vestors to
deposit equal installments ann ually at the end of eac h year. If in terest of
7.5% is paid, how much does the man need to save each y ear in order to
meet his target?
Solution: We first calculate s
10
e
, whic h is equal to
(1.075)
10
− 1
0.075
=14.1471.
10

Then the required amount of installm ent is
P =
100,000
s
10
e
=
100,000
14.1471
=$7,068.59.
2
11

2.2 Annuit y-Due
• An ann uit y-due is an annu ity for w hich the pay ments are ma de at
the beginning of the pa ym ent periods
• The first pa ym ent is made at time 0, and the last payment is made
at time n − 1.
• We denote the present value of the ann uity-due at time 0 b y ¨a
n
e
i
(or
¨a
n
e
), and the futu re value of the annuity at time n by ¨s
n
e
i
(or ¨s
n
e
).
• The formula for ¨a
n
e
can be derived as follo w s
¨a
n
e
=1+v + ···+ v
n−1
=
1 − v
n
1 − v
=
1 − v
n
d
. (2.3 )
12


• Also, w e ha v e
¨s
n
e
=¨a
n
e
× (1 + i)
n
=
(1 + i)
n
− 1
d
. (2.4 )
• As eac h pa ym ent in an annuit y-due is paid one period ahead of the
correspondin g payment of an annuity-imm ed iate, the present value
of each pa ym ent in an annuit y-due is (1+i) times of the presen t value
of the corresponding pa ym ent in an annuit y-immediate. Hence,
¨a
n
e
=(1+i) a
n
e
(2.5 )
and, similarly,
¨s
n
e
=(1+i) s
n
e
. (2.6 )
13

• As an annuit y-due of n paym ents consists of a paym ent at time 0
and an ann uity-imm ediate of n − 1 payments, the first payment of
whichistobemadeattime1,wehave
¨a
n
e
=1+a
n−1
e
. (2.7 )
• Similarly, if we consid er an annuity-im mediate with n +1 pa ym ents
at time 1, 2, ···, n +1as an annuity-due of n paym ents starting at
time 1 plus a final pa ymen t at time n +1, w e can conclude
s
n+1
e
=¨s
n
e
+1. (2.8 )
Example 2.6: A company wants to provide a retirement plan for an
employ ee who is aged 55 no w . The plan will pro vide her with an annuity-
imm ediate of $7,000 every y ear for 15 y ears upon her retirement at the
14

age of 65. The company is funding this plan with an annuity-due of 10
years.Iftherateofinterestis5%,whatistheamountofinstallmentthe
comp any should pay?
Solution: We first calculate the present value of the retirement annuit y.
Th is is equa l to
7,000 a
15
e
= 7,000 ×
"
1 − (1.05)
−15
0.05
#
=$72,657.61.
This amount should be equal to the future value of the com pany’s install-
men ts P ,whichisP ¨s
10
e
.Nowfrom(2.4),wehave
¨s
10
e
=
(1.05)
10
− 1
1 − (1.05)
−1
=13.2068,
so that
P =
72,657.61
13.2068
=$5,501.53.
15

2.3 Perpetuity, Deferred Annuity and Annuit y
Values at Other Times
• A perpetuity is an an nuity with no ter min at io n da te, i.e., n →∞.
• An example that resembles a perpetuity is the dividends of a pre-
ferred stock.
• To calculate the present value of a perpetuit y, we note that, as v<1,
v
n
→ 0 as n →∞. Thus, from (2.1 ), we have
a
∞
e
=
1
i
. (2.9 )
• For the case when the first pa ym ent is made immediately, w e ha ve,
from (2.3),
¨a
∞
e
=
1
d
. (2.10)
16

• A deferred ann uity is on e for w h ich the first paym ent starts some
time in the future.
• Co n sid e r an annuity w ith n unit pa ym ents for whic h the first pay-
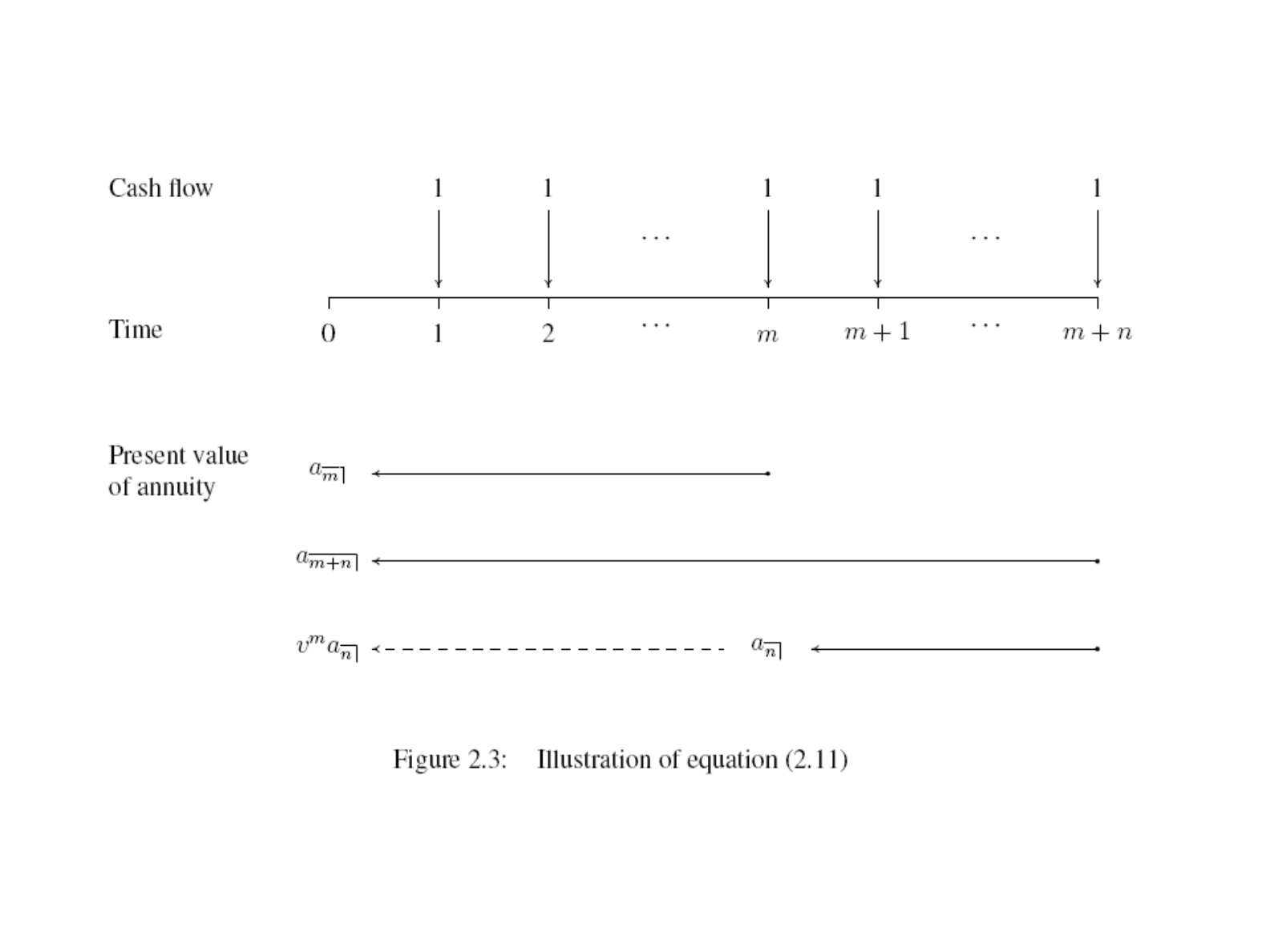
m e nt is du e at time m +1.
• This can be regarded as an n-period ann uity-imm ediate to start at
time m,anditspresentvalueisdenotedby
m|
a
n
e
i
(or
m|
a
n
e
for short).
Th us, w e ha ve
m|
a
n
e
= v
m
a
n
e
= v
m
×
∙
1 − v
n
i
¸
=
v
m
− v
m+n
i
=
(1 − v
m+n
) − (1 − v
m
)
i
17

= a
m+n
e
− a
m
e
. (2.11)
• To understand the abo ve equation, see Figure 2.3.
• From (2.11), we have
a
m+n
e
= a
m
e
+ v
m
a
n
e
= a
n
e
+ v
n
a
m
e
. (2.12)
• Multiplying the abo ve equations throughout by 1+i,wehave
¨a
m+n
e
=¨a
m
e
+ v
m
¨a
n
e
=¨a
n
e
+ v
n
¨a
m
e
. (2.13)
• We also denote v
m
¨a
n
e
as
m|
¨a
n
e
,whichisthepresentvalueofan-
payment annuit y of unit amounts due at time m, m+1, ···,m+n−1.
18

• If we multiply the equations in (2.12) throughout b y (1 + i)
m+n
,we
obtain
s
m+n
e
=(1+i)
n
s
m
e
+ s
n
e
=(1+i)
m
s
n
e
+ s
m
e
. (2.14)
• See Figure 2.4 for illustration.
• It is also straightfo rwa rd to see that
¨s
m+n
e
=(1+i)
n
¨s
m
e
+¨s
n
e
=(1+i)
m
¨s
n
e
+¨s
m
e
. (2.15)
• We now return to (2.2) and write it as
s
m+n
e
=(1+i)
m+n
a
m+n
e
,
19


so that
v
m
s
m+n
e
=(1+i)
n
a
m+n
e
, (2.16)
for arbitrary positiv e integers m and n.
• How do y ou interpret this equation?
20


2.4 A nnuities Under O ther Accumulation M ethods
• We ha ve so far discussed the calculations of the present and future
va lu e s of annuities assu min g compou n d inter est .
• We now extend our discussion to other interest-accumulation meth-
ods.
• We consider a general accumulation function a(·) and assume that
the function applies to any cash-flow transactions in the future.
• As stated in Section 1.7, an y payment at time t>0 starts to accu-
mulate interest according to a(·) as a pa yment made at time 0.
• Given the accumulation function a(·), the presen t value of a unit
payment due at time t is 1/a(t), so that the present value of a n-
21

period annuity-imm ediate of unit payments is
a
n
e
=
n
X
t=1
1
a(t)
. (2.17)
• The future value at time n of a unit paym ent at time t<nis
a(n − t), so that the future value of a n-period annuity-im m ed iate
of unit pa ym en ts is
s
n
e
=
n
X
t=1
a(n − t). (2.18)
• If (1.35) is satisfied so that a(n −t)=a(n)/a(t) for n>t>0,then
s
n
e
=
n
X
t=1
a(n)
a(t)
= a(n)
n
X
t=1
1
a(t)
= a(n) a
n
e
. (2.19)
• This result is satisfied for the compound-in terest method, but not
the simple-interest method or other accumulation sc hem es for which
equation (1.35) does not hold.
22

Example 2.7: Suppose δ(t)=0.02t for 0 ≤ t ≤ 5, find a
5
e
and s
5
e
.
Solution: We first calculate a(t), which, from (1.26), is
a(t)=exp
µ
Z
t
0
0.02sds
¶
=exp(0.01t
2
).
Hence, from (2.17),
a
5
e
=
1
e
0.01
+
1
e
0.04
+
1
e
0.09
+
1
e
0.16
+
1
e
0.25
=4.4957,
and, from (2.18),
s
5
e
=1+e
0.01
+ e
0.04
+ e
0.09
+ e
0.16
=5.3185.
Note that a(5) = e
0.25
=1.2840,sothat
a(5) a
5
e
=1.2840 × 4.4957 = 5.7724 6= s
5
e
.
23

2
• Note that in the abov e example, a(n − t)=exp[0.01(n − t)
2
] and
a(n)
a(t)
=exp[0.01(n
2
− t
2
)],
so that a(n − t) 6= a(n)/a(t) and (2.19) does not hold.
Example 2.8: Calculate a
3
e
and s
3
e
if the nominal rate of interest is
5% per ann um , assuming (a) compound interest, and (b) simple in terest.
Solution: (a) Assuming compound interest, we hav e
a
3
e
=
1 − (1.05)
−3
0.05
=2.723,
and
s
3
e
=(1.05)
3
× 2.72 = 3.153.
24

(b) For simple interest, the present value is
a
3
e
=
3
X
t=1
1
a(t)
=
3
X
t=1
1
1+rt
=
1
1.05
+
1
1.1
+
1
1.15
=2.731,
andthefuturevalueattime3is
s
3
e
=
3
X
t=1
a(3 − t)=
3
X
t=1
(1 + r(3 − t)) = 1.10 + 1.05 + 1.0=3.150.
At the same nominal rate of interest, the compound-interest m ethod gen-
erates higher in terest than the sim ple-interest m ethod. Therefore, the
future value under the compound-in terest method is higher, w hile its
present value is lower. Also, note that for the sim ple-interest method,
a(3) a
3
e
=1.15 × 2.731 = 3.141, w hich is different from s
3
e
=3.150. 2
25

2.5 Pa ym en t Periods, Compounding Periods and
Continuous Annuities
• We no w consider the case where the pa ym ent period differs from the
interest-conversion period.
Example 2.9: Find the present value of an ann uit y-due of $200 per
quarter for 2 years, if interest is compounded m onthly at the nominal rate
of 8%.
Solution: Thisisthesituationwherethepaymentsaremadeless
freq u e ntly th a n inter est is converte d . We first calculate the effective rate
of interest per quarter, whic h is
∙
1+
0.08
12
¸
3
− 1=2.01%.
26

As there are n =8payments, the required presen t value is
200 ¨a
8
e
0.0201
=200×
"
1 − (1.0201)
−8
1 − (1.0201)
−1
#
=$1,493.90.
2
Example 2.10: Find the present value of an ann uity-imm ediate of
$100 per quarter for 4 years, if interest is compounded semiannually at
the nominal rate of 6%.
Solution: This is the situation where paymen ts are made more fre-
quently than in terest is con verted. We first calculate the effective rate of
in terest per quarter, whic h is
∙
1+
0.06
2
¸
1
2
− 1=1.49%.
27

Thus, the required present value is
100 a
16
e
0.0149
=100×
"
1 − (1.0149)
−16
0.0149
#
=$1,414.27.
2
• It is possible to derive algebraic formulas to compute the presen t
and future values of annuities for whic h the period of installment is
different from the period of compounding.
• We first consider the case where payments are made less frequently
than interest con version, which occurs at time 1, 2, ···,etc.
• Let i denote the effective rate of interest per in terest-conversion pe-
riod. Suppose a m-payment ann uity-imm ediate consists of unit pay-
men ts at time k, 2k, ···, mk.Wedenoten = mk,whichisthe
number of interest-conversion periods for the annuity.
28

• Figure 2.6 illustrates the cash flows for the case of k =2.
• Thepresentvalueoftheaboveannuity-immediateis(weletw = v
k
)
v
k
+ v
2k
+ ···+ v
mk
= w + w
2
+ ···+ w
m
= w ×
∙
1 − w
m
1 − w
¸
= v
k
×
∙
1 − v
n
1 − v
k
¸
=
1 − v
n
(1 + i)
k
− 1
=
a
n
e
s
k
e
, (2.20)
and the future value of the annuity is
(1 + i)
n
a
n
e
s
k
e
=
s
n
e
s
k
e
. (2.21)
29

• We no w consider the case where the payments are made more fre-
quently than interest con version.
• Let there be mn pa ym ents for an ann uity-imm ediate occurring at
time 1/m, 2/m, ···, 1, 1+1/m, ···, 2, ···, n,andleti be the effective
rate of interest per in terest-conversion period. Thus, there are mn
payments ov er n interest-con version periods.
• Suppose eac h payment is of the amount 1/m, so that there is a
nominal am ount of unit pa ym ent in eac h interest-conv ersion period.
• Figure 2.7 illustrates the cash flows for the case of m =4.
• We denote the present value of this annuity at time 0 by a
(m)
n
e
i
,which
can be computed as follows (we let w = v
1
m
)
a
(m)
n
e
i
=
1
m
³
v
1
m
+ v
2
m
+ ···+ v + v
1+
1
m
+ ···+ v
n
´
30


=
1
m
(w + w
2
+ ···+ w
mn
)
=
1
m
∙
w ×
1 − w
mn
1 − w
¸
=
1
m
"
v
1
m
×
1 − v
n
1 − v
1
m
#
=
1
m
"
1 − v
n
(1 + i)
1
m
− 1
#
=
1 − v
n
r
(m)
, (2.22)
where
r
(m)
= m
h
(1 + i)
1
m
− 1
i
(2.23)
is the equivalent nom inal rate of in terest compounded m tim es per
interest-conversion period (see (1.19)).
31

• The future value of the annuit y-im mediate is
s
(m)
n
e
i
=(1+i)
n
a
(m)
n
e
i
=
(1 + i)
n
− 1
r
(m)
=
i
r
(m)
s
n
e
. (2.24)
• The abov e equation parallels (2.22), wh ich can also be written as
a
(m)
n
e
i
=
i
r
(m)
a
n
e
.
• If the mn-payment annuity is due at time 0, 1/m, 2/m, ···,n−1/m,
we den o t e its present valu e at tim e 0 by ¨a
(m)
n
e
,whichisgivenby
¨a
(m)
n
e
=(1+i)
1
m
a
(m)
n
e
=(1+i)
1
m
×
∙
1 − v
n
r
(m)
¸
. (2.25)
32

• Th us, from (1.22) w e conclude
¨a
(m)
n
e
=
1 − v
n
d
(m)
=
d
d
(m)
¨a
n
e
. (2.26)
• The future value of this ann uit y at time n is
¨s
(m)
n
e
=(1+i)
n
¨a
(m)
n
e
=
d
d
(m)
¨s
n
e
. (2.27)
• For deferred annuities, the follo w ing results apply
q|
a
(m)
n
e
= v
q
a
(m)
n
e
, (2.28)
and
q|
¨a
(m)
n
e
= v
q
¨a
(m)
n
e
. (2.29)
Exam ple 2.11: Solv e the problem in Example 2.9 using (2.20).
33

Solution: We first note that i =0.08/12 = 0.0067.Nowk =3and
n =24so that from (2.20), the present value of the annuity-im mediate is
200 ×
a
24
e
0.0067
s
3
e
0.0067
=200×
"
1 − (1.0067)
−24
(1.0067)
3
− 1
#
=$1,464.27.
Finally, the presen t value of the annuit y-due is
(1.0067)
3
× 1,464.27 =$1,493.90.
2
Example 2.12: Solv e the problem in Example 2.10 using (2.22) and
(2.23).
Solution: Note that m =2and n =8.Withi =0.03,wehave,from
34

(2.23)
r
(2)
=2× [
√
1.03 − 1] = 0.0298.
Therefore, from (2.22), we have
a
(2)
8
e
0.03
=
1 − (1.03)
−8
0.0298
=7.0720.
As the total pa ym ent in eac h in terest-conversion period is $200, the re-
quired present value is
200 × 7.0720 = $1,414.27.
2
• Now we consider (2.22) again. Suppose the ann uities are paid con-
tinuously attherateof1unitperinterest-conversionperiodover
n periods. Thus, m →∞and we denote the presen t value of this
continuous annuity by ¯a
n
e
.
35

• As lim
m→∞
r
(m)
= δ,wehave,from(2.22),
¯a
n
e
=
1 − v
n
δ
=
1 − v
n
ln(1 + i)
=
i
δ
a
n
e
. (2.30)
• Thepresentvalueofan-period continuous annuit y of unit payment
perperiodwithadeferredperiodofq is given by
q|
¯a
n
e
= v
q
¯a
n
e
=¯a
q+n
e
− ¯a
q
e
. (2.31)
• To compute the future value of a continuous annuit y of unit pa ym ent
per period over n per iods , we us e the following formula
¯s
n
e
=(1+i)
n
¯a
n
e
=
(1 + i)
n
− 1
ln(1 + i)
=
i
δ
s
n
e
. (2.32)
• Wenowgeneralizetheaboveresultstothecaseofageneralaccu-
mulation function a(·). The present value of a continuous ann uit y
36

of unit pa ym ent per period o ver n periods is
¯a
n
e
=
Z
n
0
v(t) dt =
Z
n
0
exp
µ
−
Z
t
0
δ(s) ds
¶
dt. (2.33)
• To compute the future value of the ann uit y at tim e n,weassume
that, as in Section 1.7, a unit payment at tim e t accumulates to
a(n − t) at time n,forn>t≥ 0.
• Th us, the future value of the ann uit y at time n is
¯s
n
e
=
Z
n
0
a(n − t) dt =
Z
n
0
exp
µ
Z
n−t
0
δ(s) ds
¶
dt. (2.34)
37

2.6 Varying A nnuities
• We consider ann uities the pa ym ents of which vary according to an
ar it h metic pr ogr e ss io n .
• Th us, w e consider an ann uit y-imm ediate and assume the initial pay-
men t is P , with subsequen t payments P + D, P +2D, ···,etc.,so
that the jth pa ym ent is P +(j − 1)D.
• We allow D to be negative so that the ann uity can be either stepping
up or stepping down.
• Ho w ev er, for a n-payment annuity, P +(n − 1)D must be positive
so that negative cash flow is ruled out.
• We can see that the ann uit y can be regarded as the sum of the
follo w ing annuities: (a) a n-period annuit y -imm ediate with constant
38

amount P ,and(b)n −1 deferred ann uities, where the jth deferred
annuit y is a (n − j)-period annuit y-imm ediate with lev el amoun t D
tostartattimej,forj =1, ···,n− 1.
• Th us, the presen t value of the varying annuity is
Pa
n
e
+ D
⎡
⎣
n−1
X
j=1
v
j
a
n−j
e
⎤
⎦
= Pa
n
e
+ D
⎡
⎣
n−1
X
j=1
v
j
(1 − v
n−j
)
i
⎤
⎦
= Pa
n
e
+ D
⎡
⎣
³
P
n−1
j=1
v
j
´
− (n − 1)v
n
i
⎤
⎦
= Pa
n
e
+ D
⎡
⎣
³
P
n
j=1
v
j
´
− nv
n
i
⎤
⎦
= Pa
n
e
+ D
"
a
n
e
− nv
n
i
#
. (2.35)
39


• For a n-period increasing ann uit y with P = D =1,wedenoteits
present and future values by (Ia)
n
e
and (Is)
n
e
, respectively.
• It can be sho w n that
(Ia)
n
e
=
¨a
n
e
− nv
n
i
(2.36)
and
(Is)
n
e
=
s
n+1
e
− (n +1)
i
=
¨s
n
e
− n
i
. (2.37)
• For an increasing n-pa ym en t annuity-due with pa ym en ts of 1, 2, ···,n
at time 0, 1, ···,n− 1, the present value of the annuit y is
(I¨a)
n
e
=(1+i)(Ia)
n
e
. (2.38)
• This is the sum of a n-period lev el annuity-due of unit paymen ts and
a (n − 1)-pay m ent increasin g annu ity-im mediate with startin g and
incremental paym ents of 1.
40

• Th us, we ha v e
(I¨a)
n
e
=¨a
n
e
+(Ia)
n−1
e
. (2.39)
• For the case of a n-period decreasing an nuity wit h P = n and D =
−1, we denote its presen t and future values b y (Da)
n
e
and (Ds)
n
e
,
respectively.
• Figure 2.9 presen ts the tim e diagram of this annuity.
• It can be sho w n that
(Da)
n
e
=
n − a
n
e
i
(2.40)
and
(Ds)
n
e
=
n(1 + i)
n
− s
n
e
i
. (2.41)
41


• We consider two types of increasing continuous annuities. First,
we consider the case of a contin uous n-period annuity with level
payment (i.e., at a constant rate) of τ units from tim e τ −1 through
time τ .
• We denote the present value of this ann uity b y (I¯a)
n
e
,whichisgiven
by
(I¯a)
n
e
=
n
X
τ =1
τ
Z
τ
τ −1
v
s
ds =
n
X
τ =1
τ
Z
τ
τ −1
e
−δs
ds. (2.42)
• The abo ve equation can be simplified to
(I¯a)
n
e
=
¨a
n
e
− nv
n
δ
. (2.43)
• Second, we may consider a con tinuous n-period annuit y for whic h
thepaymentintheintervalt to t + ∆t is t∆t, i.e., the instantan eou s
rateofpaymentattimet is t.
42

• We denote the present value of this ann uity b y (
¯
I¯a)
n
e
,whichisgiven
by
(
¯
I¯a)
n
e
=
Z
n
0
tv
t
dt =
Z
n
0
te
−δt
dt =
¯a
n
e
− nv
n
δ
. (2.44)
• We no w consider an ann uit y-immediate with pa yments following a
geometric progression.
• Let the first pa ym ent be 1, with subsequen t pa ym ents being 1+k
times the previous one. Thus, the present value of an ann uity with
n payments is (for k 6= i)
v + v
2
(1 + k)+···+ v
n
(1 + k)
n−1
= v
n−1
X
t=0
[v(1 + k)]
t
= v
n−1
X
t=0
"
1+k
1+i
#
t
43

= v
⎡
⎢
⎢
⎢
⎢
⎣
1 −
Ã
1+k
1+i
!
n
1 −
1+k
1+i
⎤
⎥
⎥
⎥
⎥
⎦
=
1 −
Ã
1+k
1+i
!
n
i − k
. (2.45)
Exam ple 2.13: An annuit y-im m ediate consists of a first payment of
$100, with subsequent payments increased by 10% o ver the previous one
until the 10th pa ym ent, after whic h subsequent pa ym ents decreases b y 5%
over the previous one. If the effective rate of intere st is 10% per payment
period, what is the presen t value of this ann uity with 20 pa y ments?
Solution: Thepresentvalueofthefirst10paymentsis(usethesecond
44

line of (2.4 5) )
100 × 10(1.1)
−1
= $909.09.
For the next 10 pa yments, k = −0.05 and their present value at time 10
is
100(1.10)
9
(0.95) ×
1 −
µ
0.95
1.1
¶
10
0.1+0.05
=1,148.64.
Hence, the presen t value of the 20 pa ym ents is
909.09 + 1,148.64(1.10)
−10
=$1,351.94.
2
Example 2.14: An investor wishes to accumulate $1,000 at the end of
year 5. He makes level deposits at the beginning of eac h year for 5 y ears.
The deposits earn a 6% ann ual effective rate of interest, wh ich is credited
45

at the end of each year. The interests on the deposits earn 5% effective
in terest rate annually. How much does he ha ve to deposit eac h y ear?
Solution: Let the lev el annual deposit be A. The interest receiv ed at
the end of y ear 1 is 0.06A, whic h increases by 0.06A ann u ally to 5 × 0.06A
at the end of year 5. T hus, the in terest is a 5-payment increasing annuit y
with P = D =0.06A, earning ann ual in terest of 5%. Hence, we have the
equation
1,000 = 5A +0.06A(Is)
5
e
0.05
.
From (2.37) we obtain (Is)
5
e
0.05
=16.0383,sothat
A =
1,000
5+0.06 × 16.0383
=$167.7206.
2
46

2.7 Term of Annuit y
• We now consider the case where the annuity period may not be an
integer. We consider a
n+k
e
,wheren is an integer and 0 <k<1.
We note that
a
n+k
e
=
1 − v
n+k
i
=
(1 − v
n
)+
³
v
n
− v
n+k
´
i
= a
n
e
+ v
n+k
"
(1 + i)
k
− 1
i
#
= a
n
e
+ v
n+k
s
k
e
. (2.46)
• Th us, a
n+k
e
is the sum of the present value of a n-period ann uit y -
immediate with unit amount and the present value of an amount s
k
e
47

paid at tim e n + k.
Exam ple 2.15: A principal of $5,000 generates incom e of $500 at the
end of every year at an effective rate of interest of 4.5% for as long as
possib le . Ca lc u la te the ter m of th e annu ity an d discu s s the possib ilitie s of
settling the last payment.
Solution: The equation of value
500 a
n
e
0.045
= 5,000
im p lie s a
n
e
0.045
=10. As a
13
e
0.045
=9.68 and a
14
e
0.045
=10.22, the principal
can generate 13 regular pa ym ents. The inv estm ent may be paid off with
an additional amount A at the end of year 13, in which case
500 s
13
e
0.045
+ A = 5,000 (1.045)
13
,
48

wh ich imp lies A = $281.02, so that the last pa ym ent is $781.02. Alter-
nativ ely, the last pa yment B ma y be made at the end of year 14, whic h
is
B =281.02 × 1.045 = $293.67.
If we adopt the approach in (2.46), we solve k from the equation
1 − (1.045)
−(13+k)
0.045
=10,
wh ich implies
(1.045)
13+k
=
1
0.55
,
from whic h we obtain
k =
ln
µ
1
0.55
¶
ln(1.045)
− 13 = 0.58.
49

Hence, the last payment C to be paid at time 13.58 years is
C =500×
"
(1.045)
0.58
− 1
0.045
#
=$288.32.
Note that A<C<B, which is as expected, as this follows the order
of the occurrence of the payments. In principle, all three approac hes are
justified. 2
• Generally, the effective rate of interest cannot be solv ed analytically
from the equation of value. Num erical methods must be used for
this purpose.
Exam ple 2.16: A principal of $5,000 generates incom e of $500 at the
end of ev ery year for 15 y ears. W hat is the effective rate of interest?
50

Solution: The equation of value is
a
15
e
i
=
5,000
500
=10,
so that
a
15
e
i
=
1 − (1 + i)
−15
i
=10.
A simple grid searc h pro vides the following results
i a
15
e
i
0.054 10.10
0.055
10.04
0.056
9.97
A finer search provides the answer 5.556%. 2
• The Excel Solver may be used to calculate the effectiverateofin-
ter e st in E x a mple 2.1 6 .
51

• The com putation is illustrated in Exhibit 2.1.
• We en ter a guessed value of 0.05 in Cell A1 in the Excel worksheet.
• The following expression is then en tered in Cell A2:
(1 −(1 + A1)ˆ(−15))/A1, whic h computes a
15
e
i
with i equal to the
value at A1.
• We can also use the Excel function RATE to calculate the rate of
in terest that equates the presen t value of an ann uit y-imm ediate to
a given value. Specifically, consider the equations
a
n
e
i
− A =0 and ¨a
n
e
i
− A =0.
Giv en n and A,wewishtosolvefori,whichistherateofinterest
per pa ym en t period of the ann uit y -imm ediate or ann uity-due. The
use of the Excel function RATE to com pute i is desc r ibed as follow s :
52

Exhibit2.1:UseofExcelSolverforExample 2.16

Excel function: RATE(np,1,pv,type,guess)
np = n,
pv = −A,
t ype = 0 (or omitted) for ann uit y-imm ediate, 1 for ann uity-due
gu ess = star tin g valu e , set to 0.1 if om itte d
Output = i, rate of interest per pa ym ent period of the annuit y
• To use RATE tosolveforExample2.16wekeyinthefollowing:
“=RATE(15,1,-10)” .
53
